函数对象[条款18]---《C++必知必会》

　　有时需要一些行为类似于函数指针的东西，但函数指针显得笨拙、危险而且过时（让我们承认这一点）。通常最佳方式是使用函数对象（function object）取代函数指针。

　　与智能指针一样，函数对象也是一个普通的类对象。智能指针类型重载 -> 和 * （可能还有 ->* 和 .*）操作符，来模仿指针的行为；而函数对象类型则重载函数调用操作符“（）”，来创建类似于函数指针的东西。考虑如下函数对象，它的每次调用都计算众所周知的斐波拉切数列（1,1,2,3,5,8,13，...）的下一个元素值：

class Fib
{
public:
    Fib():a0_(),a1_(){}
    int operator()();
private:
    int a0_,a1_;
};
int Fib::operator()()
{
    int temp=a0_;
    a0_ = a1_;
    a1_ = temp + a1_;
    return temp;
}

　　函数对象就是常规的类对象，但是可以采用标准的函数调用语法来调用它的operator()成员（此成员可能具有多个重载版本）。

Fib fib;
cout<<"next two in series:"<<fib()<<' '<<fib() <<' '<<fib()<<' '<<fib()<<' '<<fib() <<' '<<fib()<<' '<<fib() <<' '<<fib()<<' '<<fib()<<endl;

　　fib()语法被编译器识别为对fib对象的operator()成员函数的调用，这在意思上和fib.operator()等价，但是看起来更简洁。在这个例子中，使用函数对象而不是函数或者函数指针的优势在于，用于计算斐波拉切数列下一个值的状态被存储于Fib对象自身之中。如果采用函数来实现计算功能，那么必须求助于全局或局部静态变量或其它一些基本的技巧，以便在函数调用之间保持状态，或者将状态信息明确传递给函数。还要注意的是，有别于使用静态数据的函数，我们可以拥有多个同时计算的Fib对象，且其计算过程和结果不会相互干扰。

　　还有可能并且常见的是获得虚函数指针的效果，这是通过创建一个带有虚拟operator()的函数对象层次结构而实现的。考虑一个数值积分软件，它用于计算曲线所包围面积的近似值，如图5所示。

　　　　　　　　

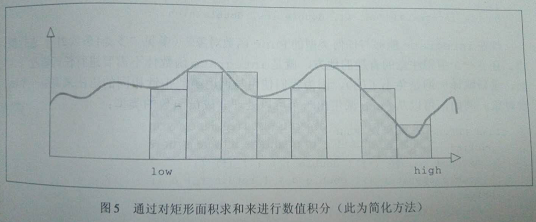
　　一个积分函数可以对 low 和 high 之间的值反复调用一个函数，来近似计算曲线所包围的面积，这是通过计算矩形面积的总和而实现的（当然也可以采用一些类似的机制）：

typedef double (*F)(double);
double integrate(F f,double low, double high){
    const int numsteps = ;
    double step = (high - low)/numsteps;
    double area = 0.0;
    while( low < high) {
        area += f(low)*step;
        low += step;
    }
    return area;
}

　　在这个版本中，传递一个函数指针来执行所期望的积分操作。

double fsinx(double x){
    return sin(x);
}
//...
cout<<"sin函数[0,π]与x轴围成的面积"<<integrate(fsinx,,PI)<<endl;

　　这可行，但不灵活，因为它使用一个函数指针来指示待整合的函数。它不能处理需要状态的函数或者指向成员函数的指针。一个代替的方式是创建一个函数对象层次结构。该层次结构的基类是一个简单的接口类，只声明了一个纯虚函数operator()。

class Func{
public:
    virtual ~Func(){};
        virtual double operator()(double) =;
};

double integrate(Func &f,double low ,double high){
    const int numsteps = ;
    double step = (high - low)/numsteps;
    double area = 0.0;
    while( low < high) {
        area += f(low)*step;
        low += step;
    }
    return area;
}

　　现在integratge能够与任何类型的Func函数对象进行整合。还有一个值得注意的有趣的地方，就是integrate函数体不需要任何修改（当然，重新编译一遍是免不了的），因为我们使用与调用函数指针相同的语法来调用一个函数对象。例如，可以从Func派生出一个可以处理非成员函数的类型：

class NMFunc:public Func{
public:
    NMFunc ( double (*f)( double )) : f_(f){}
    double operator()( double d ){return f_( d );}
private:
    double (*f_)( double );

};

　　这就允许最初版本的integrate整合所有的函数：

double fsinx(double x){
    return sin(x);
}
//...
NMFunc g(fsinx);
cout<<"sin函数[0,2/π]与x轴围成的面积"<<integrate(g,,PI/)<<endl;

　　通过为指向成员函数的指针和类对象包装一个适当的接口，还可以将成员函数整合进来：

template<class C>
class MFunc : public Func{
public:
    MFunc(C c, double (C::*f)( double ))
        :obj_(c),f_(f){};
    double operator()( double d ) { return (obj_.*f_)(d);}
private:
     C &obj_;
     double (C::*f_)( double );
};
//...
class MuFunc{
public:
    double fcos(double x){return cos(x);}
};
//...
class MuFunc{
public:
    double fcos(double x){return cos(x);}
};
//...
MuFunc mufunc;
MFunc<MuFunc> f(mufunc,&MuFunc::fcos);
cout<<"cos函数[0,π]与x轴围成的面积"<<integrate(f,,PI)<<endl;

此部分整个测试代码如下（vc++6.0）：

#include<iostream>
#include<math.h>
using namespace std;

#define PI 3.1415926

class Fib
{
public:
    Fib():a0_(),a1_(){}
    int operator()();
private:
    int a0_,a1_;
};
int Fib::operator()()
{
    int temp=a0_;
    a0_ = a1_;
    a1_ = temp + a1_;
    return temp;
}
typedef double (*F)(double);
double integrate(F f,double low, double high){
    const int numsteps = ;
    double step = (high - low)/numsteps;
    double area = 0.0;
    while( low < high) {
        area += f(low)*step;
        low += step;
    }
    return area;
}
double fsinx(double x){
    return sin(x);
}

class Func{
public:
    virtual ~Func(){};
        virtual double operator()(double) =;
};

class NMFunc:public Func{
public:
    NMFunc ( double (*f)( double )) : f_(f){}
    double operator()( double d ){return f_( d );}
private:
    double (*f_)( double );

};

double integrate(Func &f,double low ,double high){
    const int numsteps = ;
    double step = (high - low)/numsteps;
    double area = 0.0;
    while( low < high) {
        area += f(low)*step;
        low += step;
    }
    return area;
}

template<class C>
class MFunc : public Func{
public:
    MFunc(C c, double (C::*f)( double ))
        :obj_(c),f_(f){};
    double operator()( double d ) { return (obj_.*f_)(d);}
private:
     C &obj_;
     double (C::*f_)( double );
};

class MuFunc{
public:
    double fcos(double x){return cos(x);}
};

int main()
{
    Fib fib;

    cout<<fib()<<' '<<fib()<<' '<<fib()<<' '<<fib()<<' '<<fib()<<' '<<fib()<<endl;
    cout<<"next two in series:"<<fib()<<' '<<fib()
                                      <<' '<<fib()
                                      <<' '<<fib()
                                      <<' '<<fib()
                                      <<' '<<fib()
                                      <<' '<<fib()
                                      <<' '<<fib()
                                      <<' '<<fib()<<endl;

    cout<<"sin函数[0,π]与x轴围成的面积"<<integrate(fsinx,,PI)<<endl;

    NMFunc g(fsinx);
    cout<<"sin函数[0,2/π]与x轴围成的面积"<<integrate(g,,PI/)<<endl;

    MuFunc mufunc;
    MFunc<MuFunc> f(mufunc,&MuFunc::fcos);
    cout<<"cos函数[0,π]与x轴围成的面积"<<integrate(f,,PI)<<endl;
    return ;
}