图论 竞赛图(tournament)学习笔记

竞赛图(tournament)学习笔记

现在只是知道几个简单的性质。。。

竞赛图也叫有向完全图。

其实就是无向完全图的边有了方向。

​ 有一个很有趣的性质就是:一个tournament要么没有环，如果有环，那么必然有一个三元环。当然，tournament一定没有自环和二元环。

​ 证明的话，开始吧，，

​ 首先我们假定当前的tournament存在一个N元环，那么我们设A,B,C为这个N元环上连续的三个点，那么就会存在AB和BC两条边，又因为是竞赛图，所以一定会存在AC或者CA两者中的一条边。

​ 又可以开始开心地分情况讨论了：

​ (一)，存在CA边，那么很开心，我们已经找到了三元环ABC。

​ (二)，存在AC边，那么我们就会发现B这个点是没有用的了，比如这样：

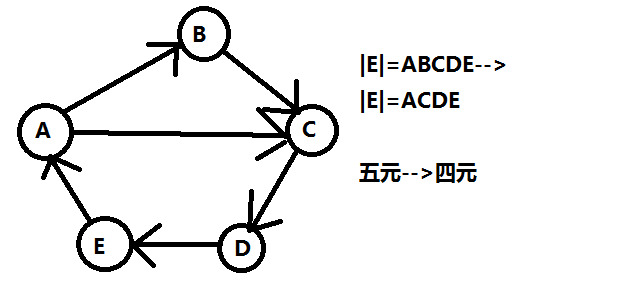
那么我们就可以把一个N元环变成N-1元环了。

那么就一定会缩小到3元环了。

上述性质例题：

CF117C Cycle

一个tournament是一个没有自环的有向图，同时，每两个点之间有一条边连接。这就是说，对于两个点u，v（u≠v），有一条从u到v的边或一条从v到u的边。

给你一个tournament，请找出一个长度为3的环。

直接按照上述性质模拟就好了。

code：

#include <iostream>
#include <cstdio>

using namespace std;

const int wx=5017;

inline int read(){
	int sum=0,f=1; char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
	while(ch>='0'&&ch<='9'){sum=(sum<<1)+(sum<<3)+ch-'0'; ch=getchar();}
	return sum*f;
}

char s[wx][wx];
int vis[wx];
int n;

bool dfs(int u,int fa){
	vis[u]=1;
	for(int i=1;i<=n;i++){
		if(s[u][i]-'0'){
			if(s[i][fa]-'0'){
				printf("%d %d %d\n",fa,u,i);
				return true;
			}
			if(!vis[i])if(dfs(i,u))return true;
		}
	}
	return false;
}

int main(){
	n=read();
	for(int i=1;i<=n;i++)
		scanf("%s",s[i]+1);
	int fl=0;
	for(int i=1;i<=n;i++)
		if(!vis[i])
			if(dfs(i,i))return 0;;
	puts("-1");
	return 0;
}

关于其他性质：

1：任意竞赛图都有哈密顿路径（经过每个点一次的路径，不要求回到出发点）。

2：竞赛图存在哈密顿回路的充要条件是强联通。

先留坑。