POJ Georgia and Bob-----阶梯博弈变形。

Georgia and Bob

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 6622		Accepted: 1932

Description

Georgia and Bob decide to play a self-invented game. They draw a row of grids on paper, number the grids from left to right by 1, 2, 3, ..., and place N chessmen on different grids, as shown in the following figure for example: 

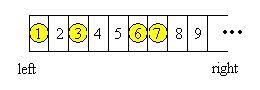
Georgia and Bob move the chessmen in turn. Every time a player will choose a chessman, and move it to the left without going over any other chessmen or across the left edge. The player can freely choose number of steps the chessman moves, with the constraint that the chessman must be moved at least ONE step and one grid can at most contains ONE single chessman. The player who cannot make a move loses the game.

Georgia always plays first since "Lady first". Suppose that Georgia and Bob both do their best in the game, i.e., if one of them knows a way to win the game, he or she will be able to carry it out.

Given the initial positions of the n chessmen, can you predict who will finally win the game?

Input

The first line of the input contains a single integer T (1 <= T <= 20), the number of test cases. Then T cases follow. Each test case contains two lines. The first line consists of one integer N (1 <= N <= 1000), indicating the number of chessmen. The second line contains N different integers P1, P2 ... Pn (1 <= Pi <= 10000), which are the initial positions of the n chessmen.

Output

For each test case, prints a single line, "Georgia will win", if Georgia will win the game; "Bob will win", if Bob will win the game; otherwise 'Not sure'.

Sample Input

2
3
1 2 3
8
1 5 6 7 9 12 14 17

Sample Output

Bob will win
Georgia will win

Source

POJ Monthly--2004.07.18

 /*

 如上如图所示：排成直线的格子上有n个格子，棋子i在左数第pi个格子上。
 G和B轮流选择一个棋子向左移动。每次移动可以移动一格及以上任意多个格，
 但是不允许超其他的格子，也不允许将两个棋子放在同一个格子内。
 无法移动就失败了。~~

 转化：
 如果将棋子两两看出一个整体考虑，我们就可以把这个游戏转为Nim游戏。
 先将棋子的个数的奇偶分情况讨论。
      偶数：___1____5____8______10
      就可以转化为  第一堆 5-1-1=3 个
                    第二堆 10-8-1=1 个。

      为什么能这样转化？
      考虑其中的一对棋子，将右边的棋子向左移动就相当于从Nim的石子堆中
      取走石子
      另一方面，将左边的棋子向左移动，石子的数量就增加了。这就与Nim不同。
      但是，即便对手增加了石子的数量，只要将所加部分减回去就回到了原来的
      状态；即便增加了石子的数量，只要对手将所加的部分减回去也就回到原来
      状态了。

      奇数：将最左边的0看出起始点就转化成偶数个了。
 */

 #include<iostream>
 #include<cstdio>
 #include<cstdlib>
 #include<algorithm>
 using namespace std;

 int f[];
 int main()
 {
     int T,n,i,k,hxl;
     while(scanf("%d",&T)>)
     {
         while(T--)
         {
             scanf("%d",&n);
             for(i=;i<=n;i++)
             scanf("%d",&f[i]);
             if(n%==)
             f[++n]=;
             k=;
             sort(f+,f++n);
             for(i=n;i>=;i=i-)
             k=k^(f[i]-f[i-]-);
             if(k==)
             printf("Bob will win\n");
             else printf("Georgia will win\n");
         }
     }
     return ;
 }