fzyzojP3782 -组合数问题

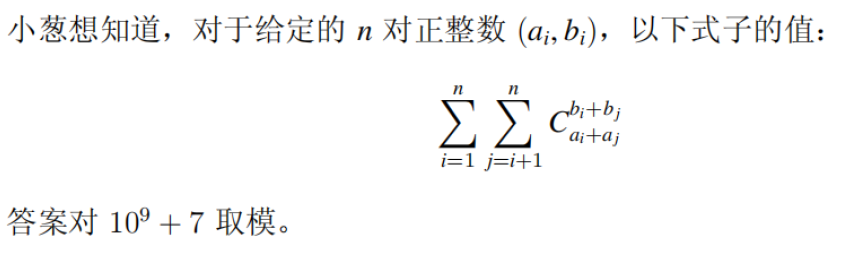
这个ai<=2000有点意思

启发我们用O(W^2)的算法

FFT不存在，对应关系过紧

考虑组合意义转化建模，再进行分离

（除以2不需要逆元不懂为啥，但是算个逆元总不费事）

由于终点可能在起点的右下，所以，从左上到右下要再做一遍

但是每个终点正上方的起点统计了两次，再减掉即可

（注意大力卡常：

1.s2[i][j]没有，就不用算了

2.f，ans开long long 尽量减少取模

3.组合数用阶乘计算

）

#include<bits/stdc++.h>
#define il inline
#define reg register int
#define numb (ch^'0')
using namespace std;
typedef long long ll;
il void rd(int &x){
    char ch;bool fl=false;
    while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true);
    for(x=numb;isdigit(ch=getchar());x=x*+numb);
    (fl==true)&&(x=-x);
}
namespace Miracle{
const int N=+;
const int M=+;
const int mod=1e9+;
ll f[N][N];
int s1[N][N],s2[N][N];
int jie[N],inv[N];
int qm(int x,int y){
    int ret=;
    while(y){
        if(y&) ret=(ll)ret*x%mod;
        x=(ll)x*x%mod;
        y>>=;
    }
    return ret;
}
ll mo1(ll x){
    return x>=4e12?x%mod:x;
}
ll mo2(ll x){
    return x>=?x%mod:x;
}
int n;
int C(int n,int m){
    return (ll)jie[n]*inv[m]%mod*inv[n-m]%mod;
}
int main(){
    rd(n);
    int a,b;
    jie[]=;
    for(reg i=;i<=;++i) jie[i]=(ll)jie[i-]*i%mod;
    inv[]=qm(jie[],mod-);
    for(reg i=;i>=;--i) inv[i]=(ll)inv[i+]*(i+)%mod;
    ll ans=;
    for(reg i=;i<=n;++i){
        rd(a);rd(b);
        int x=a-b+,y=b+;
        s1[x][y]++;
        x=-a+b+,y=-b+;
        s2[x][y]++;
        ans=mo2(ans+mod-C(*a,*b));
    }
    ans%=mod;
///    cout<<ans<<endl;
    for(reg i=4000;i>=1;--i){
        for(reg j=;j>=;--j){
            f[i][j]=mo1(f[i+][j]+f[i][j+]+s1[i][j]);
            if(s2[i][j])ans=mo2(ans+(ll)f[i][j]*s2[i][j]);
        }
    }
    ans%=mod;
//    cout<<ans<<endl;
    for(reg i=;i<=;++i){
        for(reg j=;j>=;--j){
            f[i][j]=mo1(f[i-][j]+f[i][j+]+s1[i][j]);
            ans=s2[i][j]?(ans+(ll)f[i][j]*s2[i][j])%mod:ans;
            s1[i][j]+=s1[i][j+];
            ans=s2[i][j]?(ans-(ll)s1[i][j]*s2[i][j]+(ll)*mod)%mod:ans;
        }
    }
    ll inv2=5e8+;
    ans=ans*inv2%mod;
    printf("%lld",ans);
    return ;
}

}
signed main(){
    freopen("3782.in","r",stdin);
    freopen("3782.out","w",stdout);
    Miracle::main();
    return ;
}

/*
   Author: *Miracle*
   Date: 2019/2/8 18:52:17
*/

总结：

核心：转化问题，分离终点和起点

和这个题的最后差分分离思路有异曲同工之处：AGC 018E.Sightseeing Plan——网格路径问题观止