统计学习方法：CART算法

作者：桂。

时间：2017-05-13  14:19:14

链接：http://www.cnblogs.com/xingshansi/p/6847334.html

、

---

前言

内容主要是CART算法的学习笔记。

CART算法是一个二叉树问题，即总是有两种选择，而不像之前的ID3以及C4.5B可能有多种选择。CART算法主要有回归树和分类树，二者常用的准则略有差别：回归树是拟合问题，更关心拟合效果的好坏，此处用的是均方误差准则; 分类树是分类问题，更像是离散变量的概率估计，用与熵类似的Gini系数进行度量。

一、CART算法——回归树

因为是回归问题，只要抓住两个要点就好：

1）如何切分;

2）切分后的不同区域，如何取值;

先来分析一下一次划分的操作：

　　A-回归树切分

选择第j个变量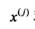和它的取值s，作为切分变量和切分点，并定义两个区域：

通过寻找最小均方误差点，实现切分：

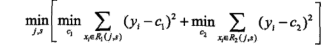
　　B-回归树的输出值

对固定输入变量j找到最优切分点s，并定义各自区域均值为输出变量：

　　C-回归树举例

看一下习题中的例子：

数据的切分点分别为：1.5，2.5，3.5，4.5，5.5，6.5，7.5，8.5，9.5

从公式

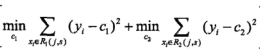
可以看出输出值c就是对应类别内y的均值。

当切分点选择s = 2.5时，区域R1有：

c1 = (4.5+4.75)/2=4.625

区域R2有：

同样c2 = 7.17

从而计算出s = 2.5对应的估计误差：

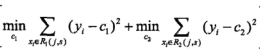
不同的s切分点，对应的估计误差不同，最后选择最小误差对应的切分点，这就完成了一次切分：

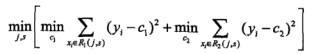
此时的c1,c2分别对应两类输出值。

假设s=6.5处实现了第一次划分，第二次就是分别在子区域进一步划分，如将：

进行二次切分，步骤思路与上面完全一致。

总结一下CART回归树的算法思路：

二、CART算法——分类树

　　A-基尼系数

CART分类树不再是基于信息增益，而是引入了Gini系数，给出基尼系数定义：

二分问题中Gini系数与熵之半的对比：

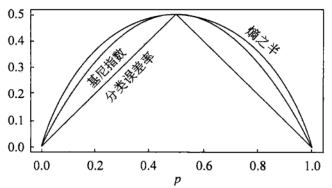
可以看出基尼系数与熵的特性类似，也是不确定性（信息量）的一种量度。

一方面，如果对于样本集合D，基尼系数：

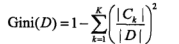
其中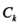是D中属于第k类的样本子集，K是类的个数。

如果D被特征A划分为D1、D2两部分，这个时候就是统计均值，D的基尼系数：

　　B-CART决策树生成

CART决策树的生成，抓住两个基本要点：

1）基尼系数计算，确定二叉树；

2）确定决策树层次结构

举例说明：

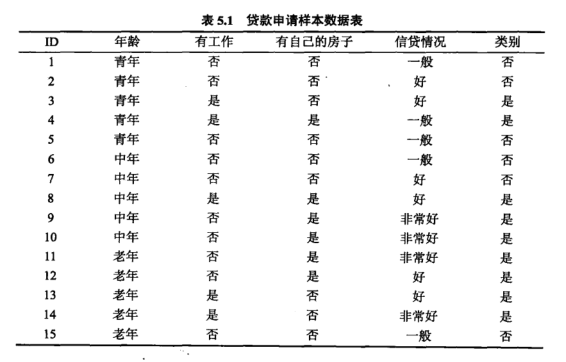
分别以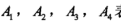表示年龄、有工作、有自己的房子、信贷情况。

对于A1是分为中年、老年、青年，计算基尼系数

A1、A3都可以，选择A1，，即青年是一类，非青年（中年、老年）是一类，

有工作、有自己的房子，都是二分，可以不用切分。信贷情况A4：

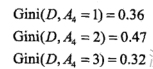
最小，故选为最优切分点。

至此，完成了基尼系数计算以及二叉树划分。下面确定决策树层次结构：

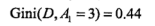
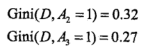
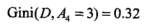
由小到大，A3为最优切分点，依次在A1，A2，A4选择，故选择A2为次优切分点......依次类推。

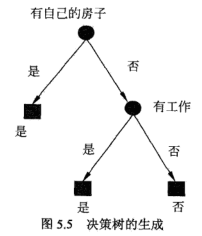
给出决策树生成算法：

主要分两步走：

1）计算各种情况的基尼系数，划分每个节点的二叉树;

2）根据基尼系数的大小，确定二叉树不同节点的层次结构，形成决策树。

 

三、CART树剪枝

回归树（拟合问题）与决策树都存在过拟合问题，防止过拟合（过渡细化）都需要剪枝的操作。

先来看看剪枝用到的准则函数：

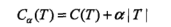
关于C(T)之前文章有分析，它是叶节点特性的度量，C4.3里它是熵的均值，CART决策树里它是基尼系数的概率均值，原理类似。多一个正则项，就是稀疏性约束。

ID3、C4.5算法中的剪枝原理是给定α，事实上很难一次给出理想的α。CART剪枝不再给定一个α，然后选择最优决策树，而是通过设定不同的α，通过交叉验证选择最优CART树，也就是：

训练集：得到不同的子树;

测试集：交叉验证选择最优树.

从有限个子树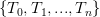中计算最优子树，最优子树由验证集得出的测试误差决定，哪个最小就是哪个。

这里就引出了一个问题，每次剪哪一个节点呢？先看分析剪枝的两个极端情况：

1）完全没剪：

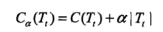
2）只剩根节点：

在α较小或者为0时，有：

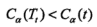
在α取+∞大时，有：

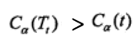
α是连续变量，因此总有临界点：

为了不混淆变量，重新定义：

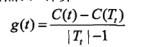
α大于g(t)就是该剪。简而言之：

对于同一棵树的结点，α都是一样的，当α从0开始缓慢增大（或者从+∞慢慢减小），总会有某棵子树该剪，其他子树不该剪的情况，即α超过了某个结点的g(t)，但还没有超过其他结点的g(t)。这样随着alpha不断增大，不断地剪枝，就得到了n+1棵子树，接下来只要用独立数据集测试这n+1棵子树，试试哪棵子树的误差最小 就知道那棵是最好的方案了。

给出CART剪枝算法：

原书的算法勘误：

（4）修改为：

（6）修改为：

参考：

• 李航《统计学习方法》