混沌数学之二维logistic模型
上一节讲了logistic混沌模型,这一节对其扩充一下讲二维 Logistic映射.它起着从一维到高维的衔接作用,对二维映射中混沌现象的研究有助于认识和预测更复杂的高维动力系统的性态。通过构造一次藕合和二次祸合的二维Logistic映射研究了二维Logistic映射通向混沌的道路,分析了其分形结构和吸引盆的性质,指出选择不同的控制参数,二维映射可分别按Feigenbaum途径等走向混沌,并且指出在控制参数空间中的较大的区域。
二维滞后Logistic映射的数学方程为: x(n+1)=y(n);y(N+1)=u*y(n)*(1-x(n)), u属于(0,2.28),[x,y]属于(0,1)
相关DEMO参见:混沌数学之离散点集图形DEMO
其代码与上一节的代码很相似:
// http://www.baike.com/wiki/logistic%E6%A8%A1%E5%9E%8B
class Logistic2DEquation : public DiscreteEquation
{
public:
Logistic2DEquation()
{
m_StartX = 0.5f;
m_StartY = m_StartX; m_ParamA = 2.003f;
} void IterateValue(float x, float y, float& outX, float& outY) const
{
outX = y;
outY = m_ParamA*y*(-x);
} bool IsValidParamA() const {return true;}
};
其图形与上一节的大不一样:
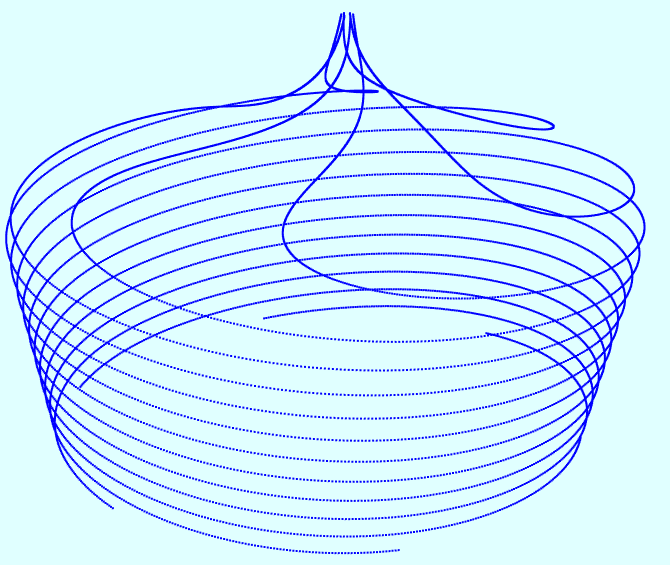


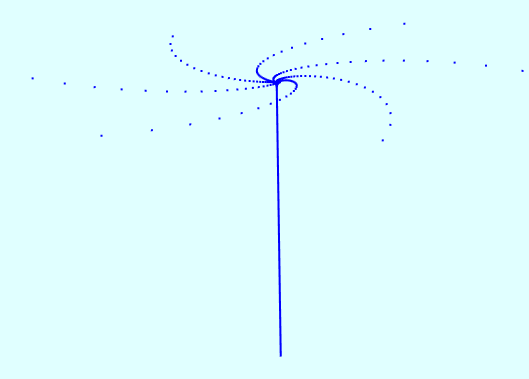
混沌数学之二维logistic模型的更多相关文章
- Luogu P2822 [NOIp2016提高组]组合数问题 | 数学、二维前缀和
题目链接 思路:组合数就是杨辉三角,那么我们只要构造一个杨辉三角就行了.记得要取模,不然会爆.然后,再用二维前缀和统计各种情况下组合数是k的倍数的方案数.询问时直接O(1)输出即可. #include ...
- 混沌数学之离散点集图形DEMO
最近看了很多与混沌相关的知识,并写了若干小软件.混沌现象是个有意思的东西,同时混沌也能够生成许多有意思的图形.混沌学的现代研究使人们渐渐明白,十分简单的数学方程完全可以模拟系统如瀑布一样剧烈的行为.输 ...
- Halcon的二维码解码步骤和解码技巧
一.二维码简介 1 . 类型多样,常见的有QR Code二维码. Data Matrix二维码等. 2.高密度编码,信息容量大. 3.容错能力强,具有纠错功能:二维码因穿孔.污损等引起局部损坏时,照样 ...
- Java 创建/识别条形码、二维码
条形码(Barcode)是将宽度不等的多个黑条和空白,按照一定的编码规则排列,用以表达一组信息的图形标识符.常用于标示物品的生产国.制造厂家.商品名称.生产日期.图书分类号.邮件起止地点.类别.日期等 ...
- 混沌数学之logistic模型
logistic回归又称logistic回归分析,主要在流行病学中应用较多,比较常用的情形是探索某疾病的危险因素,根据危险因素预测某疾病发生的概率. 相关DEMO参见:混沌数学之离散点集图形DEMO ...
- 混沌数学之CircuitChaotic(二维离散电路混沌系统)
相关软件参见:混沌数学之离散点集图形DEMO 相关代码: // http://wenku.baidu.com/link?url=yg_gE7LUXCg2mXRp-ZZdfRXXIkcNj8YOhvN7 ...
- 混沌数学之Arnold模型
相关软件混沌数学之离散点集图形DEMO 相关代码: class ArnoldEquation : public DiscreteEquation { public: ArnoldEquation() ...
- C++二级指针第二种内存模型(二维数组)
C++二级指针第二种内存模型(二维数组) 二维数组 二维数组本质上是以数组作为数组元素的数组,即“数组的数组”. 定义 类型说明符 数组名[常量表达式][常量表达式] 例如: float a[3][4 ...
- C语言提高 (3) 第三天 二级指针的三种模型 栈上指针数组、栈上二维数组、堆上开辟空间
1 作业讲解 指针间接操作的三个必要条件 两个变量 其中一个是指针 建立关联:用一个指针指向另一个地址 * 简述sizeof和strlen的区别 strlen求字符串长度,字符数组到’\0’就结束 s ...
随机推荐
- 请爱护你的JTAG烧录口---记录
排除了下载线的问题后,还是不能访问FPGA的JTAG口,那么很有可能你的FPGA芯片的JTAG口已经损坏.此时请用万用表检查TCK,TMS,TDO和Tdi是否和GND短路,如果任何一个信号对地 ...
- Java中面向对象的理解
按照惯例,先做一个简单的介绍,现在开始学习 Thinging in Java 4 ,一边看,一边记录,我都不想给自己设定时间安排了,毕竟很少实现过.所以就这样吧!不定期的更新,我都会放到博客中的. 所 ...
- 交换机高级特性MUX VLAN
MUX VLAN 基本概念 lMUX VLAN(Multiplex VLAN)提供了一种通过VLAN进行网络资源控制的机制. 例如,在企业网络中,企业员工和企业客户可以访问企业的服务器. 对于企业来说 ...
- redis 发布/订阅 模式
发布/订阅模式的命令如下: * 进入发布订阅模式的客户端,不能执行除发布订阅模式以上命令的其他命令,否则出错.
- 使用UniBeast安装Hackintosh(黑苹果)
前期准备 UniBeast 原版macOS Sierra安装包,由于苹果并没有提供完整dmg的下载地址,我也不在此提供,大家可以从信任的途径取得,文件后缀必须为dmg. 16GB或者更大的U盘 至少2 ...
- iOS Sprite Kit教程之场景的切换
iOS Sprite Kit教程之场景的切换 Sprite Kit中切换场景 每一个场景都不是单独存在的.玩家可以从一个场景中切换到另外一个场景中.本小节,我们来讲解场景切换.在每一个游戏中都会使用到 ...
- dataTransfer 对象
dataTransfer 对象 提供了对于预定义的剪贴板格式的访问,以便在拖曳操作中使用. DHTML元素属性列表 属性 描述 dropEffect 设置或获取拖曳操作的类型和要显示的光标类型. ef ...
- mysql 通过cmd 在命令行创建数据库
一.连接MYSQL 格式: mysql -h主机地址 -u用户名 -p用户密码 1. 连接到本机上的MYSQL. 首先打开DOS窗口,然后进入目录mysql\bin,再键入命令mysql -u roo ...
- Minimum Size Subarray Sum 最短子数组之和
题意 Given an array of n positive integers and a positive integer s, find the minimal length of a suba ...
- CSS选择器复习
通用选择器:* 选择到所有的元素 选择子元素:> 选择到元素的直接后代(第一级子元素) 相邻兄弟选择器:+ 选择到紧随目标元素后的第一个元素 普通兄弟选择器:~ 选择到紧随其后的所有兄弟元素 伪 ...
