谱聚类（Spectral clustering）（1）：RatioCut

作者：桂。

时间：2017-04-13  19:14:48

链接：http://www.cnblogs.com/xingshansi/p/6702174.html

声明：本文大部分内容来自：刘建平Pinard博客的内容。

---

前言

　　之前对非负矩阵分解（NMF）简单梳理了一下，总觉得NMF与聚类非常相似，像是谱聚类的思想。在此将谱聚类的知识梳理一下，内容无法转载，不然直接转载刘建平Pinard的博文了，常用的谱聚类有RatioCut和Ncut算法，全文主要梳理RatioCut算法：

　　1）背景知识；

　　2）理论推导；

　　3）应用实例

内容为自己的学习记录，其中参考他人的部分，最后一并给出链接。

一、背景知识

关于图的基本概念，以及常用到的拉普拉斯矩阵，之前已经有博文介绍过。直接从图的分割说起：

　　A-邻接矩阵

邻接矩阵的构造方法，常用的有KNN、全连接等方法，这里仅以全连接中的高斯核为例：

$W_{ij}=S_{ij}=exp(-\frac{||x_i-x_j||_2^2}{2\sigma^2})$

　　B-无向图切图

对于无向图$G$的切图，我们的目标是将图$G(V,E)$切成相互没有连接的k个子图，每个子图点的集合为：$A_1,A_2,..A_k$它们满足$A_i \cap A_j = \emptyset$,且$A_1 \cup A_2 \cup ... \cup A_k = V$。

对于任意两个子图点的集合$A, B \subset V$，$A \cap B =  \emptyset$，我们定义A和B之间的切图权重为：

$W(A, B) = \sum\limits_{i \in A, j \in B}w_{ij}$

那么对于我们k个子图点的集合：$A_1,A_2,..A_k$,我们定义切图cut为：

$cut(A_1,A_2,...A_k) = \frac{1}{2}\sum\limits_{i=1}^{k}W(A_i, \overline{A}_i )$

其中$\overline{A}_i$为${A}_i$的补集。

那么如何切图可以让子图内的点权重和高，子图间的点权重和低呢？一个自然的想法就是最小化$cut(A_1,A_2,...A_k)$，但是可以发现，这种极小化的切图存在问题，如下图：

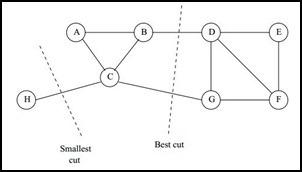
找到类似图中"Best Cut"这样的最优切图呢？一个自然的想法就是，类似为了防止过拟合而添加正则项一样，可以添加新的限定，这就是谱聚类的思想。

二、理论推导（RatioCut）

定义$|A_i|$: = 子集$A_i$中点的个数。现在对每个切图，不光考虑最小化$cut(A_1,A_2,...A_k)$，它还同时考虑最大化每个子图点的个数，即：

$RatioCut(A_1,A_2,...A_k) = \frac{1}{2}\sum\limits_{i=1}^{k}\frac{W(A_i, \overline{A}_i )}{|A_i|}$

那么怎么最小化这个RatioCut函数呢？牛人们发现，RatioCut函数可以通过如下方式表示。

我们引入指示向量$h_j =\{h_1, h_2,..h_k\}\; j =1,2,...k$，对于任意一个向量$h_j$它是一个n维向量（n为样本数），我们定义$h_{ji}$为：

$h_{ji}= \begin{cases} 0& { v_i \notin A_j}\\ \frac{1}{\sqrt{|A_j|}}& { v_i \in A_j} \end{cases}$

借助拉普拉斯矩阵特性，我们对于$h_i^TLh_i$有：

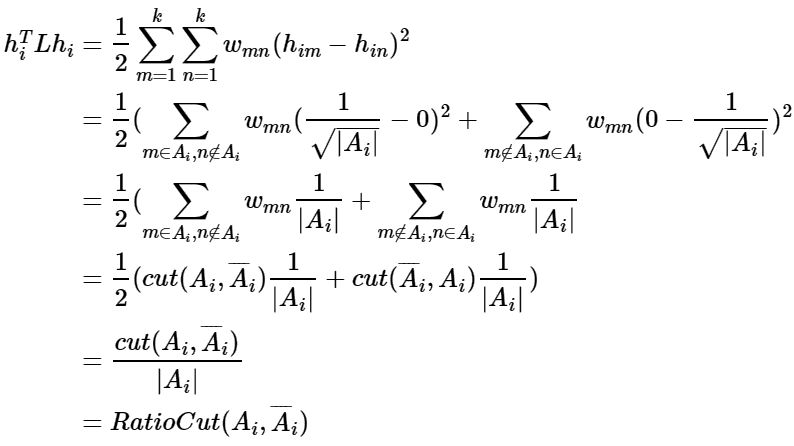
可以看出，对于某一个子图i，它的RatioCut对应于$h_i^TLh_i$，那么我们的k个子图呢？对应的RatioCut函数表达式为：

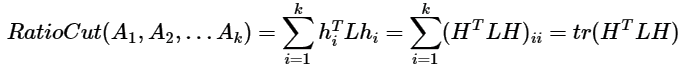
注意到$H^TH=I$，优化函数转化为：

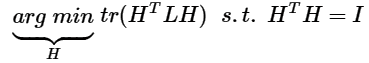
因为每一个h的取值有两种可能，因此该准则函数需要k*2ⁿ种H，这是一个NP难问题。

如果对条件适当放松呢？比如这样：

h不再看作只有两种取值的离散变量，而是具有连续取值的变量。

这样一来，上面的优化函数就可以对h利用拉格朗日乘子法进行求解。这种求解方法是瑞利熵求解的一类，关于瑞利熵前文有介绍。因为这里放宽了h的限定，使得h从离散量变为连续量，如何与之前的对应呢？最简单的办法就是看求解的h离h原始的两个取值，哪个更近，对应的就算做哪一类。离哪个更近？没错，这正是Kmeans的思想，故后处理也可以用调Kmeans来完成。Kmeans之前，通常将求解的h每一列分别归一化。

至此完成了RatioCut的步骤。

三、代码实现

首先根据上文的理论分析，给出RatioCut的算法步骤：

步骤一：求解拉普拉斯矩阵L

步骤二：对L进行特征值分解，并取K个最小特征值对应的特征向量（K为类别数目）

步骤三：将求解的K个特征向量（并分别归一化），构成新的矩阵，对该矩阵进行Kmeans处理

Kmeans得到的类别标签，就是原数据的类别标签，至此完成RatioCut聚类。

给出对应代码：

sigma2 = 0.002;
%%Step1: Calculate Laplace matrix
for i = 1:N
    for j =1:N
        W(i,j) = exp(-sqrt(sum((X(i,:)-X(j,:)).^2))/2/sigma2);
    end
end
W = W-diag(diag(W));% adjacency matrix
D = diag(sum(W)); %degree matrix
L = D-W;%laplace matrix
%%Step2:Eigenvalues decomposition
K = 3;
[Qini,V] = eig(L);
%%Step3:New matrix Q
[~,pos] = sort(diag(V),'ascend');
Q = Qini(:,pos(1:K));
Q = Q./repmat(sqrt(diag(Q'*Q)'),N,1);
[idx,ctrs] = kmeans(Q,K);

测试一下，按数据为3类进行谱聚类，可以看出来还是有效的，谱聚类中高斯权重涉及到$\sigma$如何取值，不过这里就不做进一步讨论了。

参考：

• http://www.cnblogs.com/pinard/p/6221564.html