AVL树、splay树(伸展树)和红黑树比较

一、AVL树：

优点：查找、插入和删除，最坏复杂度均为O(logN)。实现操作简单

如过是随机插入或者删除，其理论上可以得到O(logN)的复杂度，但是实际情况大多不是随机的。如果是随机的，则AVL 树能够达到比RB树更优的结果，因为AVL树的高度更低。如果只进行插入和查找，则AVL树是优于RB树的，因为RB树更多的优势还是在删除动作上。

缺点：1)借助高度或平衡因子，为此需要改造元素结构，或额外封装-->伸展树可以避免。

2)实测复杂度与理论复杂度上有差距。插入、删除后的旋转成本不菲。删除操作后，最多旋转O(logN)次，(Knuth证明，平均最坏情况下概率为0.21次)，若频繁进行插入/删除操作，得不偿失。

3)单词动态调整后，全树拓扑结构的变化量可达O(logN)次。-->红黑树为O(1)

二、伸展树(splay tree)、

优点、1)无需记录节点高度和平衡因子，编程实现简单易行

2)分摊复杂度为O(logN)

3)局部性强，缓存命中率极高时，效率甚至可以更高。

注：伸展树是根据数据访问的局部性而来的主要是：1)刚刚被访问的节点，极有可能在不就之后再次被访问到；2)将被访问的下一个节点，极有可能就处于不就之前被访问过的某个节点的附近。

缺点：1)仍不能保证单词最坏情况的出现，不适用效率敏感的场合

2)复杂度分析比较复杂

三、红黑树

优点：1)所有的插入、删除、查找操作的复杂度都是O(logN)

2)插入操作能够在最多2次旋转后达到平衡状态，而删除操作更是能够在一次旋转后达到平衡状态。删除操作有可能导致递归的双黑修正，但是在旋转之前，只是染色而树的结构没有任何实质性的改变，因此速度优于AVL树。

3)红黑树可以保证在每次插入或删除操作之后的重平衡过程中，全书拓扑结构的更新仅涉及常数个节点。尽管最坏情况下需对O(logN)个节点重染色，但就分摊意义而言，仅为O(1)个。

缺点：左右子树高度相差比AVL树大。

总结

二叉查找树：

任意一个节点所包含的键值，大于等于左孩子的键值，小于等于右孩子的键值。
此外，无论是左旋还是右旋，若旋转之前这棵树是二叉查找树，旋转之后它一定还是二叉查找树。

平衡树（AVL树）：

AVL树中任何节点的两个子树的高度最大差别为1，LL,RR,LR,RL旋转算法。
对于1百万个节点的平衡树，树的高度为12-20之间，对于10亿个节点的平衡树，树的高度为18-30之间。

伸展树：

当某个节点被访问时，伸展树会通过旋转使该节点成为树根。

红黑树：

主要是用它来存储有序的数据，它的时间复杂度是O(lgn))，效率非常之高.

AVL树与红黑树比较：

AVL是严格平衡树，因此在增加或者删除节点的时候，根据不同情况，旋转的次数比红黑树要多。（所以AVL树插入和删除时间会稍微多）
红黑树是弱平衡的，用非严格的平衡来换取增删节点时候旋转次数的降低。
两者都属于自平衡二叉树，那么降低树的深度自然会提高查找效率。
两者查找，插入，删除的时间复杂度相同O(lgn)

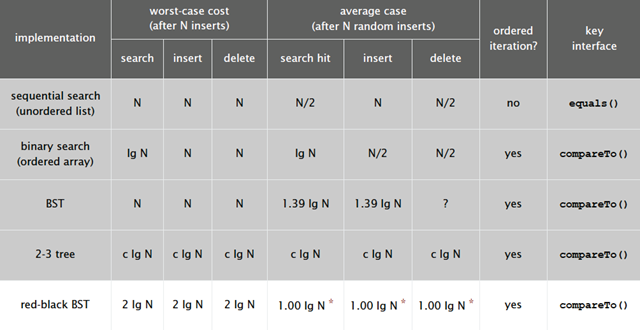
时间复杂度比较

sequential search - 顺序查找
binary search - 二分查找
BST - 二叉查找树
2-3 tree - 平衡树
red-black tree - 红黑树