[转]详细解读TrueSkill 排名系统

概要

大多数竞技游戏都有一个评价玩家是否完成目标的度量指标，它是游戏的基础。对于包含两个或两个以上玩家（多玩家比赛）的比赛，常涉及到游戏玩家技能的排名方法。游戏鼓励玩家之间相互竞争，玩家不只要赢得单场比赛，还得让更多的玩家见识和认可自己的整体技能水平。玩家可能期望能够通过认识的人或者没有一块玩过的潜在对手来评估自身技能，从而能够安排一些“有意思”的比赛。如果一场比赛，参与其中的玩家胜率极不平衡，我们则称它是“无悬念的”比赛，很少有人愿意玩一场准赢或必输的比赛。相反地，参赛选手彼此势均力敌的比赛一定是“有悬念的”比赛。

目前，人们已经设计出许多排名系统，使得游戏联盟能够比较成员的相对技能。通常，一个排名系统都包含三个要素：

• 更新模块：根据玩家之间的游戏结果，跟踪所有玩家的技能。

• 匹配模块：给成员安排有意思的比赛。

• 选手积分榜模块：识别和发布成员技能。

特别地，世界足球联盟ELO排名系统已经成功用于各种两个玩家竞技的联盟，如美国象棋联盟或世界象棋联盟，或者其他类型的联盟。在网络游戏中，许多联盟都采用每场比赛两个以上玩家参与的游戏模型。ELO并不适用于这些场景。事实上，流行的基于技能的排名系统均布支持这类游戏。人们创建出许多一次性的排名系统支持这类游戏，但它们都不是通用的，足以应用于所有这类游戏。

如何表示技能

TrueSkill排名系统是一个基于技能的排名系统，设计用于克服当前排名系统的局限，保证在联盟内确实可以安排出有意思的比赛。它使用一个名为贝叶斯推断的技术对玩家进行排名。

TrueSkill排名系统不是假设每个玩家对应一个固定的技能，它使用一个钟形信念分布（也称高斯分布）表示对玩家的信念。每个信念分布可以使用一个均值μ（峰点）和标准差σ（散度）进行唯一表示。

上图表示一个信念分布实例，技能信念分布曲线下方某个范围的区域对应玩家技能落入此区间的信念。比如，图中绿色区域是玩家技能处于等级15至20的信念。随着系统对玩家技能的了解，σ趋向于逐渐变小，玩家技能的信念范围将更加紧凑。换个角度来看μ和σ，可以分别将其视为“玩家技能的平均信念”和系统对玩家技能评估的“不确定性”。

由于TrueSkill排名系统使用一个高斯信念分布表示玩家的技能，所有玩家的平均技能（即μ）将始终（更准确地是以99.99%的概率）落在初始σ的± 4 倍区间范围。对约65万个玩家，280多万场比赛的跟踪实验数据支持这一论断：没有任何μ曾落到初始σ的± 4 倍区间范围之外，甚至99.99%的μ都落在初始σ的± 3 倍区间范围之内。

有趣的是，由于通过简单相乘就可以将μ与σ放缩到任意范围，TrueSkill排名系统可以使用数值为1的初始不确定性参数进行所有的计算。比如，假设所有的计算都使用初始值μ=3，σ=1进行。如果有人希望将玩家技能表示成50个“等级”中的一个，由于几乎所有的μ都是位于初值σ值的± 3 倍区间范围之内，将μ和σ乘以50/6=8.3即可。

TrueSkill排名系统的直观性在于两个玩家的μ值相差越大，假设两者的σ值相似，则μ值越大的玩家在游戏中表现更佳的几率就越大。这个原则在TrueSkill排名系统中始终成立。但是，它并不意味着μ值越大的玩家稳赢，而是他们赢的几率要大于μ值小的玩家。TrueSkill排名系统假设单场比赛中玩家的表现在其真实技能上下浮动，游戏结果（所有参赛选手的相对排名）是由他们的表现决定。因此，TrueSkill排名系统中一个玩家的技能可认为是其多次比赛的平均表现。在玩家技能上下波动的表现方差从原则上来说是TrueSkill排名系统的一个配置参数。

如何更新技能

TrueSkill排名系统将仅仅根据游戏结果（所有参赛团队的相对排名）更新玩家的μ值和σ值。它仅仅假设游戏结果应归于围绕玩家技能上下波动的未观测到的表现。在积分形式的游戏中，如果赢家以10分的差距击败了其他所有的玩家，则其所获得的胜利与仅仅以1分差距赢取胜利的玩家没有任何差别。每场比赛都为系统提供了更多拉低σ数值的玩家技能信念信息。在根据新游戏结果决定所有参赛玩家新的技能信念前，TrueSkill排名系统假设每个玩家的技能可能会相对于其参与的最近一次游戏发生微小的变化。此假设从数学上得到的结果是技能不确定性指标σ将略微上升，增加量原则上是TrueSkill排名系统的一个配置参数。正是这个参数不但允许TrueSkill排名系统跟踪玩家技能随时间的改善，还能保证技能不确定性指标σ始终不会降至零（维持动量）。

为了根据新游戏结果确定所有参赛玩家新的技能信念，TrueSkill排名系统得确定给定参赛玩家技能的前提下，观测到的游戏结果所发生的概率，并根据相应技能信念的概率为其赋权。这个过程通过计算所有可能表现的均值（以对应概率为权值）实现：表现最佳的玩家胜出，表现次好的排名第二，以此类推。如果两个玩家的表现十分接近，TrueSkill排名系统将认定两个玩家之间的游戏打成平局。根据TrueSkill排名系统，在一个给定联盟中判定为平局的间隔越大，则平局发生的可能性就越大。间隔的大小是TrueSkill排名系统的一个配置参数，可根据游戏模式进行调整。比如，在世界街头赛车3中的街头赛绝不会产生平局（因此参数设为0），而在完美特工:零中的夺旗游戏很容易产生平局。

根据以上赋权技术（也称贝叶斯定律），排名系统可以确定每个参赛玩家的新技能信念。这些技能信念不再服从高斯分布。因此，TrueSkill排名系统确定了最佳高斯近似。由此，给定玩家的μ值只要胜出就增加，落败则下降。如下表格给出了每个（设想）玩家在一场存在八个参赛者的比赛前后的μ和σ值。

可以看到σ值（反映每个玩家技能的不确定性）在比赛后下降，对于排在第四和第五（Darren与Eve）的玩家下降尤甚。两个玩家σ值的界是他们打败或被被打败的玩家最大数目：两人分别被3个（或4个）玩家打败，打败4个（或3个）其他玩家。与之形成对比，排在第一的玩家（Alice）显然比其他7个玩家表现都好，他们没有限制其技能的发挥：她甚至可能优于等级36.771。这个可以从值为5.749的不确定性指标中反映出来。

对于一个TrueSkill排名系统更新算法最简单的例子莫过于两个玩家的比赛。假设只有两个玩家A（Alice）和B（Bob），二者的参数μ和σ分别为(μA,σA) 和 (μB,σB)。一旦比赛结束，更新算法确定赢家（Alice或Bob）和输家（Bob或Alice），应用下面的更新方程（这里为简单起，我们不考虑出现平局的概率）：

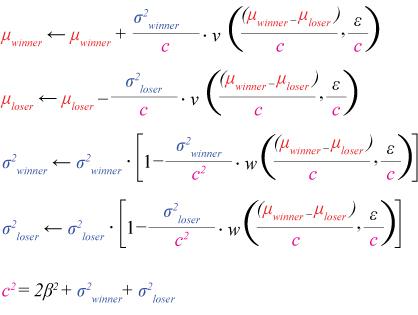
更新方程中，唯一的未知量是β2 ，它是围绕玩家表现波动的方差。此外ε 是前面提到的平局间隔，由游戏模式决定。但是函数v(.,.) 和 w(.,.) 的表达式是什么样的呢？无需给出它们的准确定义，我们来看看这些函数随ε/c变化的图像：

观察这些更新方程可以发现：

• 与ELO系统相似，在平均技能更新方程中，赢家的平均技能增加一个v((μwinner-μloser)/c,ε/c)的倍数，输家的平均技能则减去一个v((μwinner-μloser)/c,ε/c)的倍数。但是，ELO的权重因子大致正比于两个不确定指标之和（2β2是由围绕技能波动的表现方差决定，σ2winner+σ2loser 则是他们真实技能的不确定性），而TrueSkill的权重因子大致正比于winner/loser。从而，只有当Alice与Bob的不确定性相等时，TrueSkill排名系统的平均技能更新方程则退化为ELO更新方程。我们需要注意，TrueSkill排名系统的平均技能更新方程不保证零和。

• 两个玩家的不确定性指标（不管win/loss/draw)将减少1-σ2player/c2 * w((μwinner-μloser)/c,ε/c)。再次，不确定越大的玩家其下降的幅度越大。

• 如果游戏结果没有悬念，则平均技能的变化、v((μwinner-μloser)/c,ε/c)、不确定性参数减少的因子、1-σ2player/c2 * w((μwinner-μloser)/c,ε/c)都趋于零。

赢/输

如果赢家的平均技能相对全部不确定性指标大得多（由此(μwinner-μloser) > ε），则一场胜利不能为赢家带来额外的平均技能积分，或消除任何的不确定性。反之亦成立，如果游戏结果有悬念：若赢家的平均技能较小（(μwinner-μloser) < ε），可以为赢家带来或从输家扣掉正比于μloser-μwinner的平均积分。

平局

如果更新之前两个玩家的平均技能相似（由此|μwinner-μloser| < ε），则二者已经足够接近，不需要再进行平均技能积分的更新。因此，不确定性不在下降。然而，如果在比赛前TrueSkill排名系统认为某个玩家更强（即μwinner-μloser> ε），那么其平均技能将下降，对手玩家的均值增大，从而拉近两者的平均技能。

TrueSkill排名系统的平均技能更新方程与ELO算法的更新方程类似。关键差别在于主要根据两玩家的不确定指标比率使用了一个可变的K因子。由此，在TrueSkill排名系统中，相比与另一个表现不稳定的玩家比赛，与一个表现稳定的玩家比赛，将使得表现不稳定的玩家发生更大幅度的起伏。

但是TrueSkill排名系统如何融入团队比赛的结果呢？这里，团队的技能假设为团队中每个玩家的技能之和。TrueSkill排名系统的更新算法使用上述两个更新方程确定两队的技能之和，其中(μwinner,σ2winner) 和 (μwinner,σ2loser) 分别是赢家团队和输家团队的平均技能及技能方差。

对于两个以上的团队，由于涉及数值积分（上述图像通过相同的数值积分代码得到），我们不能写出更新方程的表达式。此时，TrueSkill排名算法通过对所有排在相邻位置的团队，循环迭代地进行更新，也即是说排在第一个的与排在第二的两个队，排在第二的与排在第三的两个队，依次类推。如果你想了解更多这种TrueSkill排名算法的变体，请访问我们的交互排名计算器。

如何匹配玩家

玩家配对是游戏联盟提供的一个重要服务。它允许参与者寻找队友和技能等级相当接近的对手。结果，由于所有参与者赢的几率几乎相等，比赛可能十分精彩。

TrueSkill排名系统的技能信念是基于概率结果模型，因此可以比较玩家平局的相对几率。比赛参与者的技能越一致，这种配置的玩家组合以平局收场的可能性越大，对于每个玩家比赛就显得越有趣。比如，对于两个技能信念为(μA,σA) 和 (μB,σB)的玩家A(lice) 和 B(ob)，两者比赛平局的几率可以通过下式给出：

这个数字通常位于0和1之间，其中0表示最差的可能匹配，1则表示最佳的可能匹配。即便当两个玩家的μ值相同时，则不确定性指标σ影响匹配的质量。如果σA与σB不同，则匹配质量准则显著小于1！

如何构建选手积分榜

基于两个表示对玩家技能信念的参数μ 和 σ，TrueSkill排名系统使用所谓的保守技能估计=μ -k*σ给玩家排名。这个估计之所以称作是保守的，在于它是玩家技能的一个保守的近似：玩家的真实技能极有可能大于保守估计。k值越大，则估计值越保守，通常取k=3。

引自：http://yuedu.163.com/news_reader/#/~/source?id=a89298ff-8bc7-4448-8c97-56755eba7021_1&cid=041750bdf3554196b9b1ee2029291f4f_1