局部加权回归、欠拟合、过拟合 - Andrew Ng机器学习公开课笔记1.3

本文主要解说局部加权(线性)回归。在解说局部加权线性回归之前，先解说两个概念：欠拟合、过拟合。由此引出局部加权线性回归算法。

欠拟合、过拟合

例如以下图中三个拟合模型。第一个是一个线性模型。对训练数据拟合不够好，损失函数取值较大。如图中第二个模型，假设我们在线性模型上加一个新特征

x%5E%7B2%7D" alt="" style="border:0px">项，拟合结果就会好一些。

图中第三个是一个包括5阶多项式的模型，对训练数据差点儿完美拟合。

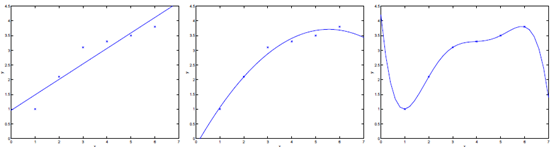
模型一没有非常好的拟合训练数据，在训练数据以及在測试数据上都存在较大误差。这样的情况称之为欠拟合（underfitting）。

模型三对训练数据拟合的非常不错，可是在測试数据上的精确度并不理想。这样的对训练数据拟合较好。而在測试数据上精确度较低的情况称之为过拟合（overfitting）。

局部加权线性回归（Locally weighted linear regression，LWR）

从上面欠拟合和过拟合的样例中我们能够体会到，在回归预測模型中。预測模型的精确度特别依赖于特征的选择。特征选择不合适。往往会导致预測结果的天差地别。局部加权线性回归非常好的攻克了这个问题，它的预測性能不太依赖于选择的特征，又能非常好的避免欠拟合和过拟合的风险。

在理解局部加权线性回归前，先回顾一下线性回归。

线性回归的损失函数把训练数据中的样本看做是平等的，并没有权重的概念。

线性回归的具体请參考《线性回归、梯度下降》，它的主要思想为：

而局部加权线性回归，在构造损失函数时增加了权重w，对距离预測点较近的训练样本给以较高的权重，距离预測点较远的训练样本给以较小的权重。权重的取值范围是(0,1)。

局部加权线性回归的主要思想是：

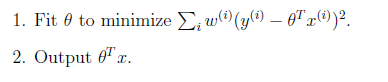
当中如果权重符合公式

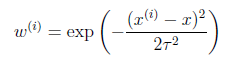
公式中权重大小取决于预測点x与训练样本的距离。假设|-
x|较小，那么取值接近于1，反之接近0。參数τ称为bandwidth。用于控制权重的变化幅度。

局部加权线性回归长处是不太依赖特征选择。并且仅仅须要用线性模型就训练出不错的拟合模型。

可是因为局部加权线性回归是一个非參数学习算法，损失数随着预測值的不同而不同，这样θ无法事先确定。每次预測时都须要扫描全部数据又一次计算θ，所以计算量比較大。