UVA 12075 Counting Triangles

https://icpcarchive.ecs.baylor.edu/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=1296

动态规划

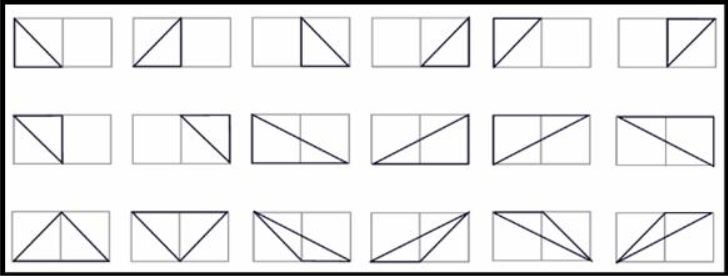
我们先计算任意三个点组成的可能，然后排除同一水平，同一垂直的，同一斜线的，前两个比较好计算，同一斜线的稍复杂.要用容斥原理，首先我们动手计算一下，可能发现每次多的是gcd(i, j)-1,然后再去重，dp[i][j]代表从左上角[0,0] 到这个点[i,j]并以这两个点为端点枚举三点共线的个数，最后还要递推一次，得到n*m的网格三点共线的个数，当然这也要*2.

参考http://blog.csdn.net/u011345136/article/details/38736595

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <vector>
#include <queue>
#include <cstdlib>
#include <iomanip>
#include <cmath>
#include <ctime>
#include <map>
#include <set>
using namespace std;
#define lowbit(x) (x&(-x))
#define max(x,y) (x>y?x:y)
#define min(x,y) (x<y?x:y)
#define MAX 100000000000000000
#define MOD 1000000007
#define pi acos(-1.0)
#define ei exp(1)
#define PI 3.141592653589793238462
#define ios() ios::sync_with_stdio(false)
#define INF 0x3f3f3f3f
#define mem(a) (memset(a,0,sizeof(a)))
typedef long long ll;
ll dp[][],n,m;
ll C(ll n,ll m)
{
    if(n<m) return ;
    ll ans=;
    for(int i=;i<m;i++)
    {
        ans=ans*(n-i)/(i+);
    }
    return ans;
}
ll gcd(ll x,ll y)
{
    return y==?x:gcd(y,x%y);
}
void init()
{
    for(int i=;i<=;i++)
    {
        for(int j=;j<=;j++)
        {
            dp[i][j]=gcd(i,j)-;
        }
    }
    for(int i=;i<=;i++)
    {
        for(int j=;j<=;j++)
        {
            dp[i][j]+=dp[i-][j]+dp[i][j-]-dp[i-][j-];
        }
    }
    for(int i=;i<=;i++)
    {
        for(int j=;j<=;j++)
        {
            dp[i][j]+=dp[i-][j]+dp[i][j-]-dp[i-][j-];
        }
    }
    printf("%d\n",dp[][]);
}
int main()
{
    init();
    int t=;
    while(scanf("%lld%lld",&n,&m)&&(n && m))
    {
        n++;m++;
        printf("Case %d: %lld\n",++t,C(n*m,)-m*C(n,)-n*C(m,)-dp[n-][m-]*);
    }
    return ;
}