广义线性模型（Generalized Linear Model）

广义线性模型（Generalized Linear Model）

http://www.cnblogs.com/sumai

1.指数分布族

我们在建模的时候，关心的目标变量Y可能服从很多种分布。像线性回归，我们会假设目标变量Y服从正态分布，而逻辑回归，则假设服从伯努利分布。在广义线性模型的理论框架中，则假设目标变量Y则是服从指数分布族，正态分布和伯努利分布都属于指数分布族，因此线性回归和逻辑回归可以看作是广义线性模型的特例。那什么是指数分布族呢？若一个分布的概率密度或者概率分布可以写成这个形式，那么它就属于指数分布族。

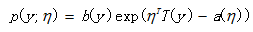
　　其中，η成为分布的自然参数（nature parameter）；T(y)是充分统计量（sufficient statistic），通常T(y)=y。当参数 a、b、T 都固定的时候，就定义了一个以η为参数的函数族。

 

2.广义线性模型（GLM）

下面我们看 GLM 的形式化定义，GLM 有三个假设：

• (1)y| x; θ 满足一个以η为参数的指数分布，那么可以求得η的表达式。
• (2) 给定x，我们的目标是要预测T(y)的期望值，大多数情况下T(y) = y，那么我们实际上要确定一个h(x)，使得h(x)=E[y| x]。
• (3)η=θ^Tx。（如果η是向量，那么η_i=θ^T_ix）

以逻辑回归作简单的例子说明，首先Y服从伯努利分布，并且写成指数分布族形式，Φ是Y=1的概率。

接着我们可以发现，T(y)=y， Φ =1/(1 + e^−η)

　

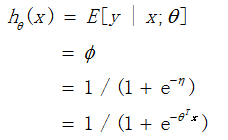
η以不同的映射函数与其它概率分布函数中的参数发生联系，从而得到不同的模型，广义线性模型正是将指数分布族中的所有成员（每个成员正好有一个这样的联系）都作为线性模型的扩展，通过各种非线性的连接函数将线性函数映射到其他空间，从而大大扩大了线性模型可解决的问题。

3. Softmax Regression

Softmax Regression是GLM的另外一个例子。假设预测值 y 有 k 种可能，即 y∈{1,2,…,k}。比如 k=3 时，可以看作是要将一封未知邮件分为垃圾邮件、个人邮件还是工作邮件这三类。

• 步骤一：

假设y服从推广的伯努利分布（多项式分布中n=1的情况），总共有k个类别，用k-1个参数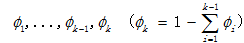代表y属于每一类的概率。

　　接着，我们要把y的分布写成指数分布族的形式。首先，先考虑伯努利分布的表达式为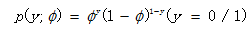：，这是y只有两个分类的情况。现在，我们的y有k个情况，这是我们引入一个示性函数1{.}（1{True} = 1, 1{False} = 0）。

那么这时候y服从分布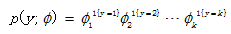：，然后我们把它写成指数分布族的形式。

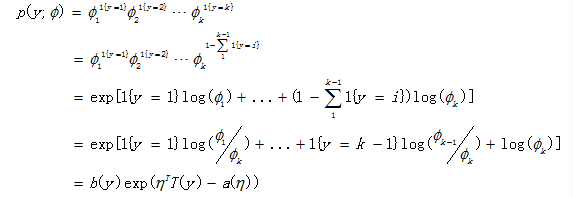  其中，

• 步骤二：

这时候，T(y)是一组 k-1 维的向量，不再是 y，如下所示：

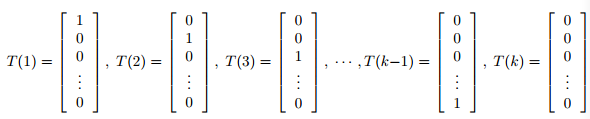
构建h_θ(x)

再用自然参数η来表示Φ

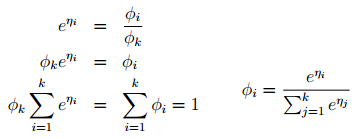
• 步骤三：

最后，用特征的线性组合去表示自然参数。

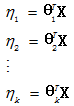
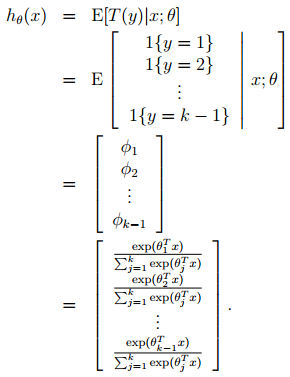
那么就建立了假设函数，最后就获得了最大似然估计

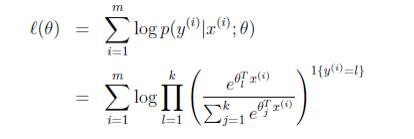
对该式子可以使用梯度下降算法或者牛顿方法求得参数θ后，使用假设函数h对新的样例进行预测，即可完成多类分类任务。对于互斥的多分类问题，这种模型比较合适，而对于非互斥的多分类问题，构建k个one-vs-all逻辑回归模型更为合适。