你真的懂TSP吗

​整数规划-模型

2022年2月26日

TSP问题

有一个邮递员，他每天负责向100个客户的家门口送一份报纸，他希望走最短的总路程来完成配送任务，这是TSP问题最原始的场景。用理论描述就是：找一个路径最小的哈密顿回路（Hamiltonian cycle） 。

哈密顿回路：也称为一笔画问题，就是从一个点出发不重复的走完所有的点，最后在回到出发点。我们现在希望为邮递员找到这个最短的哈密顿回路。

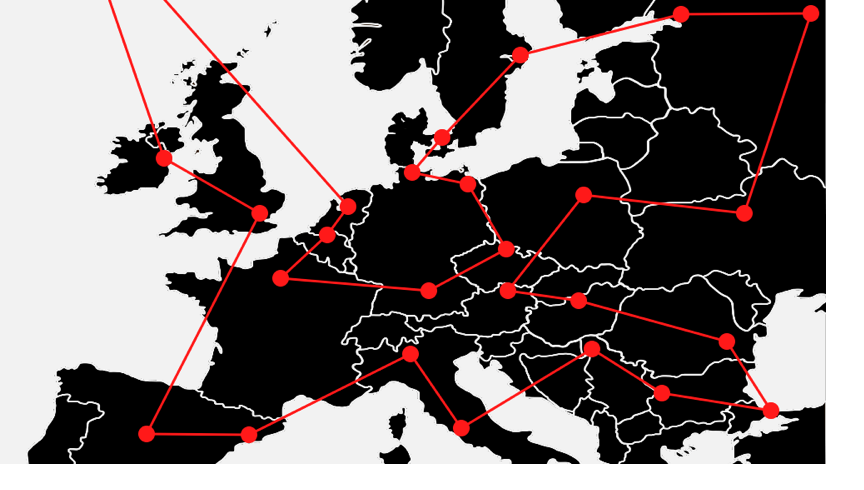
求解

关于求解TSP问题的方法，有很多，但是他们之间的效率也是千差万别，比如我们本篇推文介绍基于整数规划的一类求解思路这也是最主流的效果最好的，可以拓展到非常大的规模的一类解法，可以说是正统解法，当然还有其他解法，比如动态规划等，这里先挖一个坑，有时间小编一定把动态规划的思路的代码一同奉上。

模型

这里我们提供两个模型，分别是对称TSP和非对称TSP，假设我们我们将报亭标号为1，且客户的数量加上报亭一共为n；cij表示从i到j的距离。

分析

虽然我们把模型写出来了，但是我们必须得知道每个约束的作用是什么，只有清楚的知道当前这一步是为什么，我们才知道下一步得往哪里走，对吧。

对比：

1. 目标函数：没有区别；
2. Asymmetric的（1）（2）在Symmetric中变成了（5），这三个约束我们一般称为“度约束”。 在非对称的情况cij和cji是不同的，所以我们从i走到j和从j走到i是不同的。所以我们需要针对每个点的出度和入度进行约束；但是对称的情况则不用却分从i到j还是从j到i，为了避免求解模型的时候还是将xij和xji进行枚举，比较我们就在一开始的时候不生成从j到i得边，（这里请仔细想想，我说出来的话可能在你那里就变味了）。但是不难看出，“度约束的数量少了一半”非常哈皮啊。所以求解对称问题比求解非对称问题快你现在知道为什么了对吧。
3. Asymmetric的（3）在Symmetric中变成了（6），这两个约束可以称为“消除子环约束”，为什么需要这个约束呢？我们先把这个约束从两个模型中去掉，来看看，会发现有一种不合法的情况会出现，如如图1所示：
4. 最后（4）和（7）约束限制，决策变量必须为整数，以为一条边的存在不能是小数的。

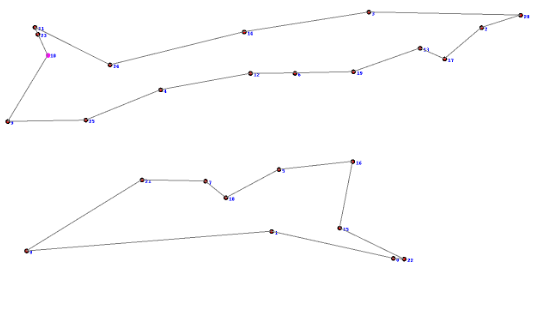
图1

这个结果显然是不对的，因为它没有做到一笔画，而是分了两笔；但是如果没有“消除子环约束”我们的模型将会把上述模型视为合法的，但是真正的最优结果应该是

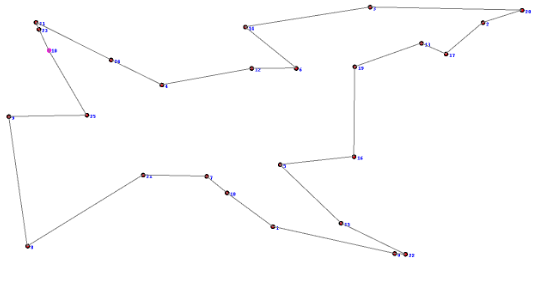
图2

在下期的推文中我们将介绍，如何借助cplex构造：割平面算法（cutting plane）和分支定界算法，来求解问题。小编到时候会提供代码哦，还不快快关注一下，哈哈哈。