Python使用函数模拟“汉诺塔”过程

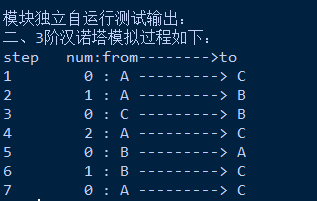
运行效果：

源代码：

 1 # -*- coding:utf-8 -*-
 2 ##汉诺塔游戏开始
 3 _times=0 #用于统计移动次数
 4 def hannuota(nlist,mfrom,mpass,mto):
 5     global _times
 6     n=len(nlist)
 7     if n==1:
 8         _times+=1
 9         print('%-8d'%_times,nlist[0],':',mfrom,'--------->',mto)
10     else:
11         hannuota(nlist[:n-1],mfrom,mto,mpass)
12         hannuota([nlist[-1]],mfrom,mpass,mto)
13         hannuota(nlist[:n-1],mpass,mfrom,mto)
14
15
16 if __name__=='__main__':
17     print("模块独立自运行测试输出：")
18     print("二、3阶汉诺塔模拟过程如下：")
19     print('step   num:from-------->to')
20     hannuota([0,1,2],'A','B','C')