「学习笔记」AC 自动机

「学习笔记」AC 自动机

点击查看目录

目录

• 「学习笔记」AC 自动机
  • 算法
    • 问题
    • 思路
    • 代码
  • 例题
    • Keywords Search
    • 玄武密码
    • 单词
    • 病毒
    • 最短母串
    • 文本生成器
    • 背单词
    • 密码
    • 禁忌

前置：「学习笔记」字符串基础：Hash，KMP与Trie。

好像对例题的讲解越来越抽象了？

算法

问题

求 \(n\) 个单词在一个长度为 \(m\) 的文章里出现过多少个。

思路

很多文章都说这玩意是 Trie 树 + KMP，我觉得确实可以这样理解但是不完全一样。

KMP 有两种理解方式：求 Border 或失配指针，AC 自动机用的是「失配指针」这个理解方式。

KMP 的失配指针指向的是一个最长的与后缀一样的前缀，这样仍然可以继续匹配，而且使需要重新匹配的地方尽量短。

AC 自动机 \(\text{fail}\) 指针指向的则是一个存在于这个 Trie 树中的最长的与真后缀相同的字符串。

依旧是拿 OI-wiki 的图举个例子：

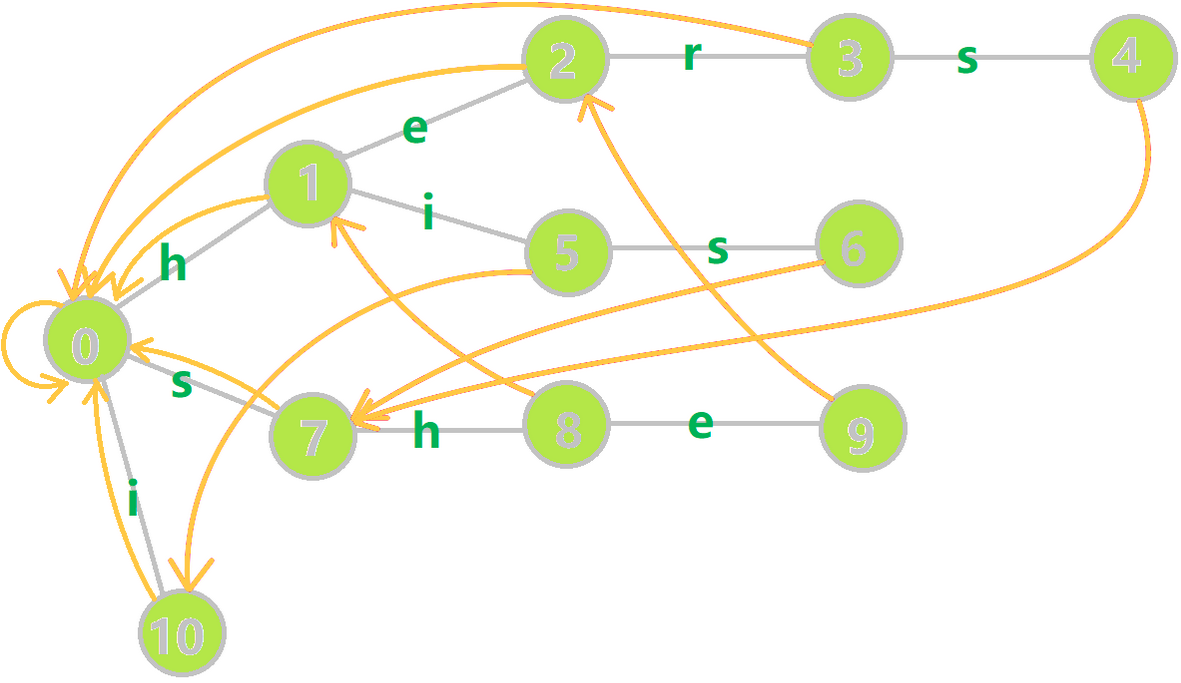
比如单词 she，它的真后缀有 he，e 和 （\(\leftarrow\) 这个真后缀是空的），其中 he 和 存在于 Trie 树中，则让 \(9\) 号节点的 \(\text{fail}\) 指针指向最长的 he 的末尾节点 \(2\) 号节点。

再如单词 her，它的真后缀有 er，r 和 ，但是只有 存在于 Trie 树中，则让 \(3\) 号节点的 \(\text{fail}\) 指针指向根节点 \(0\)。

那么怎么找到 \(\text{fail}\) 指针呢？

我们设当前节点 \(p\) 代表的字符是 \(c\)，则 \(p\) 的 \(\text{fail}\) 指针应指向 \(p\) 的父亲的 \(\text{fail}\) 指针的代表 \(c\) 的儿子。

例如上图中，\(9\) 代表的字符是 e，\(9\) 的父亲是 \(8\)，\(8\) 的 \(\text{fail}\) 指针指向 \(1\)，\(1\) 的代表 e 的儿子是 \(2\)，因此 \(9\) 的 \(\text{fail}\) 指针指向 \(2\) 号节点。

很好理解吧！xrlong said：没看出来。

但是有个问题，比如图中的六号节点应指向哪里？\(6\) 的父亲 \(5\) 的 \(\text{fail}\) 指针 \(10\) 的代表 s 的儿子不存在，但是很明显应指向 \(7\) 啊！

那就跳到 \(10\) 号节点的 \(\text{fail}\) 指针 \(0\)，找 \(0\) 的代表 s 的儿子 \(7\)。但是每次跳很多 \(\text{fail}\) 指针效率太低了，怎么办？

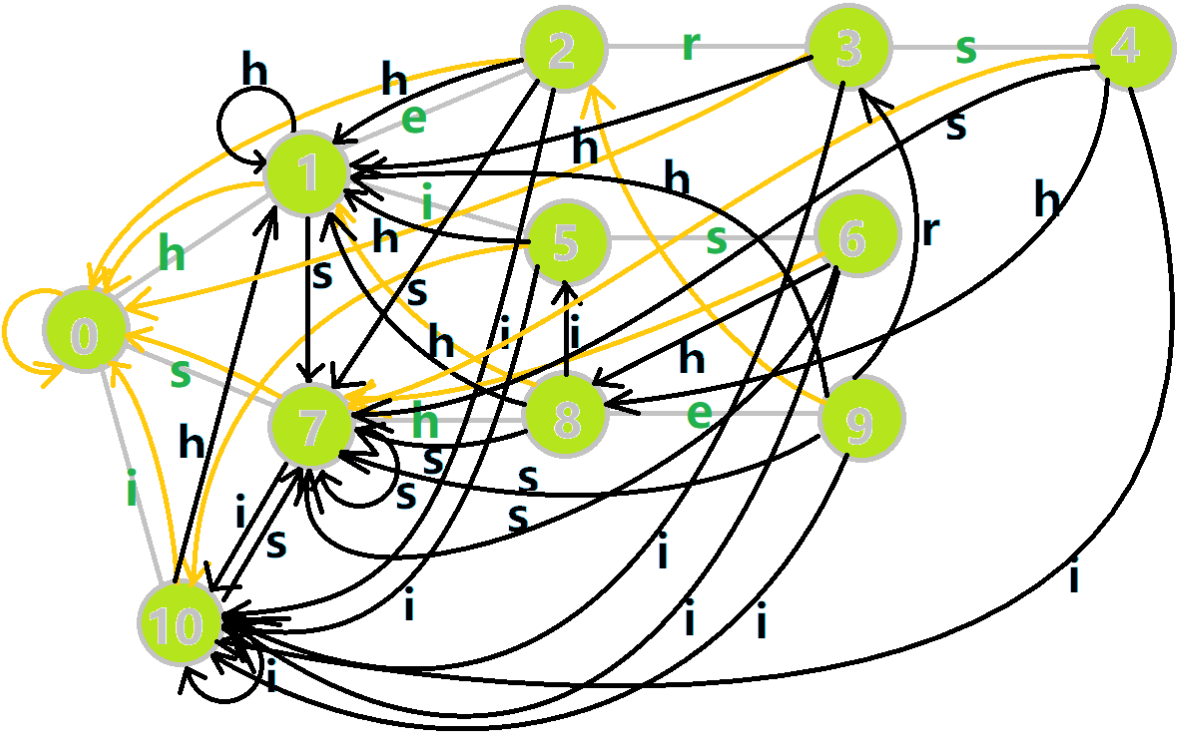
那就魔改一下这棵树！如果 \(p\) 不存在代表 \(c\) 的儿子，那就让 \(p\) 代表 \(c\) 的儿子指向 \(p\) 的 \(\text{fail}\) 指针的代表 \(c\) 的儿子。

就像下面这幅图：

最后再次放一下 OI-wiki 上的完整动图：

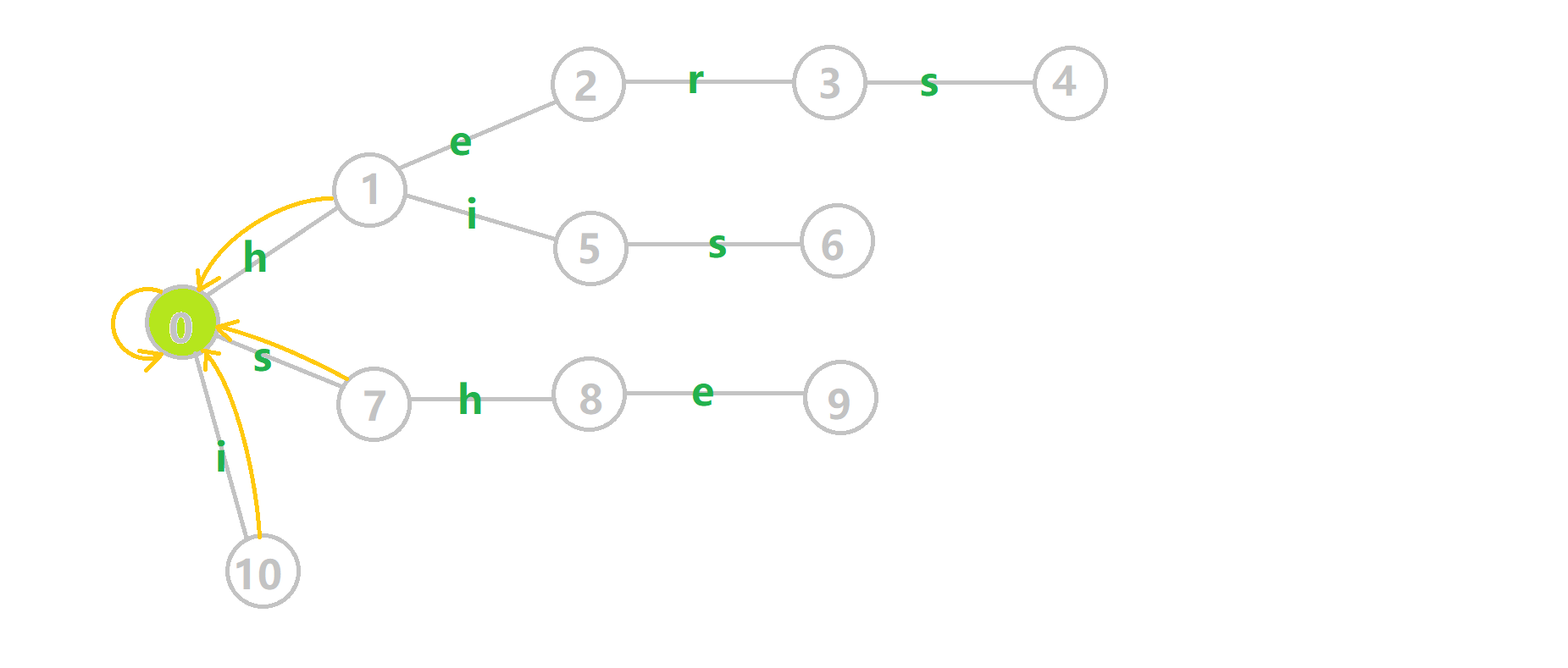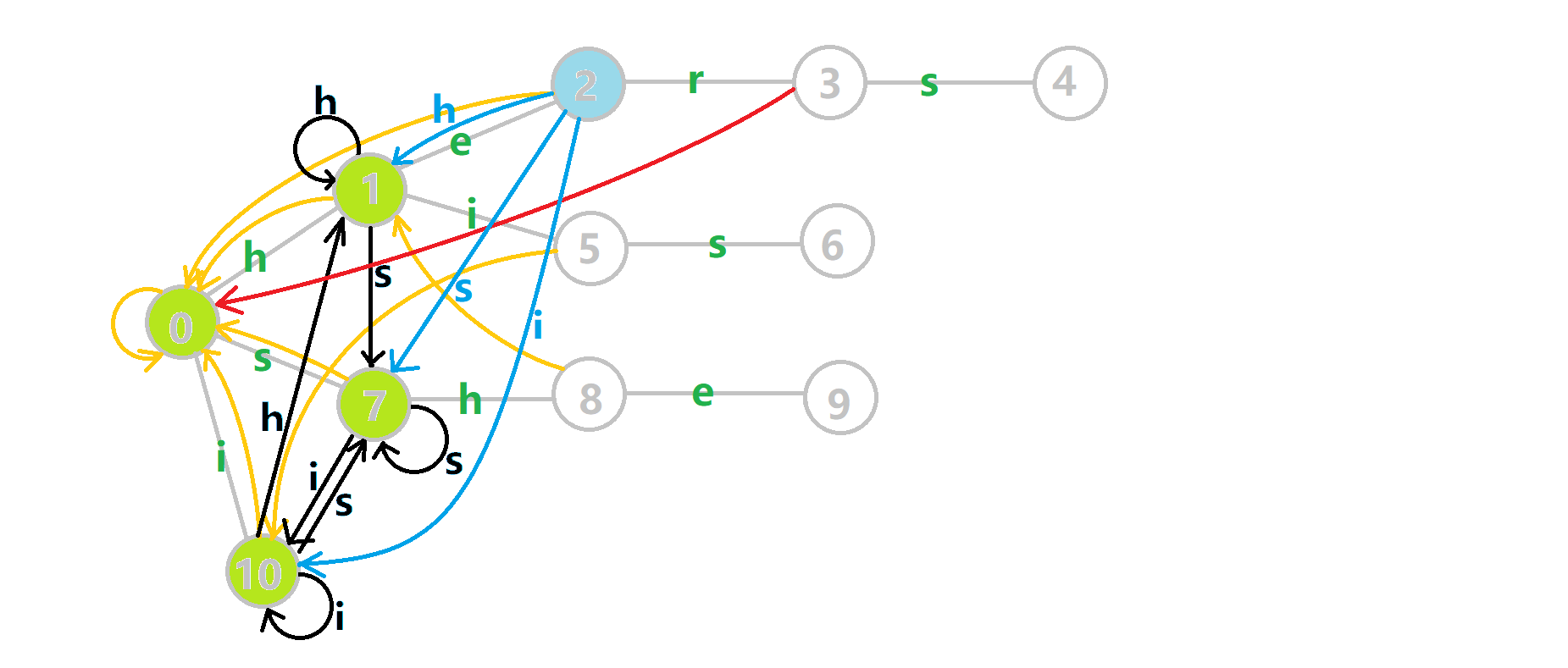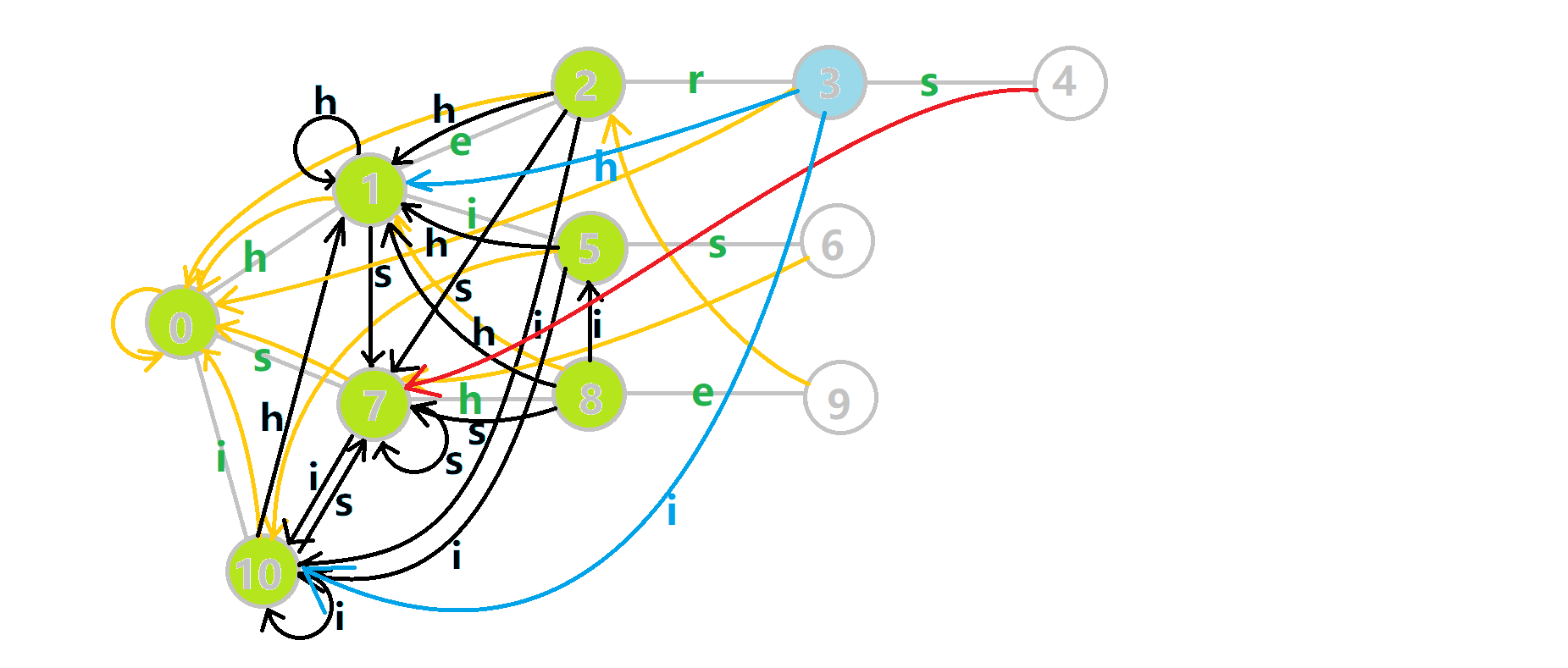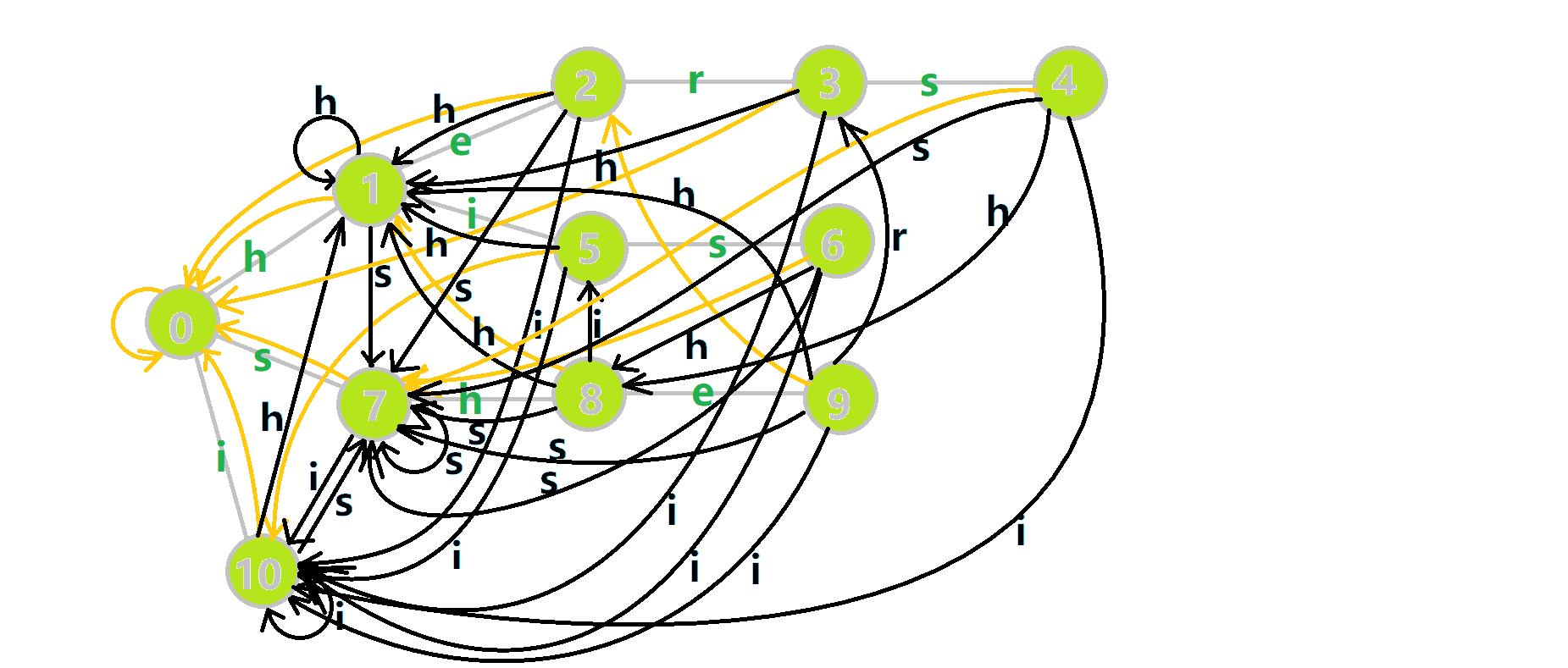
1. 蓝色结点：BFS 遍历到的结点 \(u\)。
2. 蓝色的边：当前结点下，AC 自动机修改字典树结构连出的边。
3. 黑色的边：AC 自动机修改字典树结构连出的边。
4. 红色的边：当前结点求出的 \(\text{fail}\) 指针。
5. 黄色的边：\(\text{fail}\) 指针。
6. 灰色的边：字典树的边。

代码

namespace ACAUTOMATON {
	class ACAutomaton {
	private:
		ll cnt = 0, nxt[N][26], fail[N], end[N];
	public:
		inline void Clear () {
			cnt = 0;
			memset (nxt, 0, sizeof (nxt));
			memset (end, 0, sizeof (end));
			memset (fail, 0, sizeof (fail));
			return;
		}
		inline void Insert (char* s) {
			ll p = 0, len = strlen (s + 1);
			_for (i, 1, len) {
				ll c = s[i] - 'a';
				if (!nxt[p][c]) nxt[p][c] = ++cnt;
				p = nxt[p][c];
			}
			++end[p];
			return;
		}
		inline void Build () {
			std::queue <ll> q;
			_for (i, 0, 25) if (nxt[0][i]) fail[nxt[0][i]] = 0, q.push (nxt[0][i]);
			while (!q.empty ()) {
				ll u = q.front (); q.pop ();
				_for (i, 0, 25) {
					if (nxt[u][i]) fail[nxt[u][i]] = nxt[fail[u]][i], q.push (nxt[u][i]);
					else nxt[u][i] = nxt[fail[u]][i];
				}
			}
			return;
		}
		inline ll Query (char* s) {
			ll now = 0, len = strlen (s + 1), ans = 0;
			_for (i, 1, len) {
				now = nxt[now][s[i] - 'a'];
				for (ll p = now; p && ~end[p]; p = fail[p]) ans += end[p], end[p] = -1;
			}
			return ans;
		}
	};
}

例题

Keywords Search

板子题。

玄武密码

在每个单词结尾的节点往前跑，看哪个节点深度最高且被访问过。

单词

记录每个点被访问过多少次，但直接记录时间会爆炸。

可以考虑延迟下传访问次数。

病毒

在 trie 树上找一个包括根节点的环，能找到的话直接顺着这个环不断跑就可以构造出无限长的安全代码。

最短母串

用哈希可以随便杀啊！但是这是 AC 自动机题单，所以我要用 AC 自动机写 DP（悲

\(f_{u, sta}\) 表示到节点 \(u\) 时，已经经过的字符串状态为 \(sta\) 时的最短字符串。

然后不难发现直接暴力广搜转移即可。

文本生成器

\(f_{u, l, b}\) 表示到节点 \(u\) 时，已经经过 \(l\) 个字符，「是否已经出现过给定串」的答案为 \(b(b\in\{0, 1\})\) 时的可读文本数量。

直接暴力广搜转移即可。

背单词

首先建出整个 AC 自动机，然后查询每个字符串的答案。

查询的过程有点说不太清，直接看码罢。

注意每次查询时把经过的节点标记一下，只能从标记过的节点转移。

为啥要用线段树啊。

貌似没人有我这个方法？那贴一份代码：

点击查看代码

const ll N = 3e5 + 10;

namespace ACAUTOMATON {
	class ACAutomaton {
	public:
		ll cnt = 0, nxt[N][26], jl[N], fail[N], f[N];
	public:
		inline void Clear () {
			_for (i, 0, cnt) {
				memset (nxt[i], 0, sizeof (nxt[i]));
				fail[i] = f[i] = jl[i] = 0;
			}
			cnt = 0;
			return;
		}
		inline void Insert (std::string s) {
			ll p = 0, len = s.length () - 1;
			_for (i, 0, len) {
				ll c = s[i] - 'a';
				if (!nxt[p][c]) nxt[p][c] = ++cnt;
				p = nxt[p][c];
			}
			return;
		}
		inline void Build () {
			std::queue <ll> q;
			_for (i, 0, 25) if (nxt[0][i]) fail[nxt[0][i]] = 0, q.push (nxt[0][i]);
			while (!q.empty ()) {
				ll u = q.front (); q.pop ();
				_for (i, 0, 25) {
					if (nxt[u][i]) fail[nxt[u][i]] = nxt[fail[u]][i], q.push (nxt[u][i]);
					else nxt[u][i] = nxt[fail[u]][i];
				}
			}
			return;
		}
		inline ll GetAns (std::string s, ll w) {
			ll p = 0, len = s.length () - 1, num = 0;
			_for (i, 0, len) {
				ll c = s[i] - 'a';
				jl[nxt[p][c]] = 1;
				if (jl[fail[nxt[p][c]]]) f[nxt[p][c]] = std::max (f[nxt[p][c]], f[fail[nxt[p][c]]]);
				num = std::max (num, f[nxt[p][c]]);
				p = nxt[p][c];
			}
			return f[p] = std::max (f[p], num + w);
		}
	};
}

namespace SOLVE {
	ll n, m, w[N], ans; std::string s[N];
	ACAUTOMATON::ACAutomaton ac;
	inline ll rnt () {
		ll x = 0, w = 1; char c = getchar ();
		while (!isdigit (c)) { if (c == '-') w = -1; c = getchar (); }
		while (isdigit (c)) x = (x << 3) + (x << 1) + (c ^ 48), c = getchar ();
		return x * w;
	}
	inline void In () {
		ac.Clear ();
		n = rnt (), ans = 0;
		_for (i, 1, n) {
			std::cin >> s[i], w[i] = rnt ();
			if (w < 0) continue;
			ac.Insert (s[i]);
		}
		return;
	}
	inline void Solve () {
		ac.Build ();
		_for (i, 1, n) {
			if (w[i] < 0) continue;
			ans = std::max (ans, ac.GetAns (s[i], w[i]));
		}
		return;
	}
	inline void Out () {
		printf ("%lld\n", ans);
		return;
	}
}

密码

首先如果存在一个随意填的位置，那么方案数至少为 \(52>42\)。例如：

7 2
good
day

*gooday 和 gooday* 中 * 的位置可以填 \(26\) 个字母，方案数至少为 \(2\times26=52\)。

那么只要不存在随意填的位置，输出就比较方便了。

设 \(f_{u, l, sta}\) 表示到节点 \(u\)，字符串长度为 \(l\)，已经经过的字符串状态为 \(sta\) 时的最短字符串，直接暴力广搜转移算出方案数，如果小于 \(42\) 就爆搜每种方案即可。

代码比较恶心，贴一下：

点击查看代码

namespace ACAUTOMATON {
	class ACAutomaton {
	private:
		ll cnt = 0, tot = 1, nxt[N][26], fail[N], end[N], f[N][30][M], jl[N][30][M][2];
		class APJifengc { public: ll u, l, s; };
		std::pair <ll, ll> vis[30 * 45];
		std::vector <ll> answer;
		char temp[N];
	public:
		inline void Insert (char *s, ll id) {
			ll p = 0, len = strlen (s + 1);
			_for (i, 1, len) {
				ll c = s[i] - 'a';
				if (!nxt[p][c]) nxt[p][c] = ++cnt;
				p = nxt[p][c];
			}
			end[p] |= 1 << (id - 1);
			return;
		}
		inline void Build () {
			std::queue <ll> q;
			_for (i, 0, 25) if (nxt[0][i]) fail[nxt[0][i]] = 0, q.push (nxt[0][i]);
			while (!q.empty ()) {
				ll u = q.front (); q.pop ();
				_for (i, 0, 25) {
					if (nxt[u][i]) fail[nxt[u][i]] = nxt[fail[u]][i], end[nxt[u][i]] |= end[nxt[fail[u]][i]], q.push (nxt[u][i]);
					else nxt[u][i] = nxt[fail[u]][i];
				}
			}
			return;
		}
		inline ll BFS (ll target,ll m) {
			std::queue <APJifengc> q;
			ll ans = 0; f[0][0][0] = 1;
			q.push ((APJifengc){0, 0, 0});
			while (!q.empty ()) {
				ll u = q.front ().u, l = q.front ().l, s = q.front ().s; q.pop ();
				if (l > m) break;
				if (s == target && l == m) ans += f[u][l][s];
				_for (i, 0, 25) {
					ll v = nxt[u][i], ln = l + 1, st = s | end[v];
					if (!f[v][ln][st]) q.push ((APJifengc){v, ln, st});
					f[v][ln][st] += f[u][l][s];
				}
			}
			return ans;
		}
		inline ll DFS (ll u, ll l, ll s, ll target, ll m) {
			if (jl[u][l][s][0]) return jl[u][l][s][1];
			jl[u][l][s][0] = 1;
			if (l == m) return jl[u][l][s][1] = (s == target);
			_for (i, 0, 25) jl[u][l][s][1] |= DFS (nxt[u][i], l + 1, s | end[nxt[u][i]], target, m);
			return jl[u][l][s][1];
		}
		inline void PrintAns (ll u, ll l, ll s, ll m) {
			if (!jl[u][l][s][1]) return;
			if (l == m) { puts (temp + 1); return; }
			_for (i, 0, 25) temp[l + 1] = i + 'a', PrintAns (nxt[u][i], l + 1, s | end[nxt[u][i]], m);
			return;
		}
	};
}

namespace SOLVE {
	ll n, m, ans; char s[20];
	ACAUTOMATON::ACAutomaton ac;
	inline ll rnt () {
		ll x = 0, w = 1; char c = getchar ();
		while (!isdigit (c)) { if (c == '-') w = -1; c = getchar (); }
		while (isdigit (c)) x = (x << 3) + (x << 1) + (c ^ 48), c = getchar ();
		return x * w;
	}
	inline void In () {
		m = rnt (), n = rnt ();
		_for (i, 1, n) {
			scanf ("%s", s + 1);
			ac.Insert (s, i);
		}
		return;
	}
	inline void Solve () {
		ac.Build ();
		ans = ac.BFS ((1 << n) - 1, m);
		if (ans <= 42) ac.DFS (0, 0, 0, (1 << n) - 1, m);
		return;
	}
	inline void Out () {
		printf ("%lld\n", ans);
		if (ans <= 42) ac.PrintAns (0, 0, 0, m);
		return;
	}
}

禁忌

有点像 GT 考试

设 \(f_{i, u}\) 表示长度为 \(i\)，到了节点 \(u\) 的串的期望伤害。

\[f_{i, u} = \frac{1}{alphabet}\sum_{son_{v,c} = u} f_{i - 1,v}
\]

但是 \(len\le10^9\)，不能直接转移。

于是套一下矩阵乘法就好了。

码：

点击查看代码

namespace MATRIX {
	class Matrix {
	private:
		ll n; ldb a[N][N];
	public:
		inline ldb* operator [] (ll x) { return a[x]; }
		inline void Init (ll nn) { n = nn, memset (a, 0, sizeof (a)); return; }
		inline Matrix operator * (Matrix another) const {
			Matrix ans; ans.Init (n);
			_for (i, 0, n) _for (j, 0, n) _for (k, 0, n)
				ans[i][j] += a[i][k] * another[k][j];
			return ans;
		}
		inline void Print () {
			printf ("%lld\n", n);
			_for (i, 0, n) { _for (j, 0, n) printf ("%Lf ", a[i][j]); puts (""); }
			puts ("");
			return;
		}
	};
}

namespace ACAUTOMATON {
	class ACAutomaton {
	private:
		ll cnt = 0, nxt[N][26], fail[N], end[N];
	public:
		inline void Insert (std::string s) {
			ll p = 0, len = s.length () - 1;
			_for (i, 0, len) {
				ll c = s[i] - 'a';
				if (!nxt[p][c]) nxt[p][c] = ++cnt;
				p = nxt[p][c];
			}
			end[p] = 1;
			return;
		}
		inline ll Build (ll alphabet) {
			std::queue <ll> q;
			_for (i, 0, alphabet - 1) if (nxt[0][i]) fail[nxt[0][i]] = 0, q.push (nxt[0][i]);
			while (!q.empty ()) {
				ll u = q.front (); q.pop ();
				_for (i, 0, alphabet - 1) {
					if (nxt[u][i]) fail[nxt[u][i]] = nxt[fail[u]][i], q.push (nxt[u][i]);
					else nxt[u][i] = nxt[fail[u]][i];
				}
				end[u] |= end[fail[u]];
			}
			return cnt;
		}
		inline MATRIX::Matrix GetMatrix (ll alphabet) {
			MATRIX::Matrix ma; ma.Init (cnt + 1);
			_for (i, 0, cnt) {
				_for (j, 0, alphabet - 1) {
					if (end[nxt[i][j]]) ma[i][0] += 1.0 / (ldb)(alphabet), ma[i][cnt + 1] += 1.0 / (ldb)(alphabet);
					else ma[i][nxt[i][j]] += 1.0 / (ldb)(alphabet);
				}
			}
			ma[cnt + 1][cnt + 1] = 1.0;
			return ma;
		}
	};
}

namespace SOLVE {
	ll n, m, len, alphabet;
	std::string s[N];
	MATRIX::Matrix ans;
	ACAUTOMATON::ACAutomaton ac;
	inline ll rnt () {
		ll x = 0, w = 1; char c = getchar ();
		while (!isdigit (c)) { if (c == '-') w = -1; c = getchar (); }
		while (isdigit (c)) x = (x << 3) + (x << 1) + (c ^ 48), c = getchar ();
		return x * w;
	}

	inline MATRIX::Matrix FastPow (MATRIX::Matrix a, ll b) {
		MATRIX::Matrix an; an.Init (m);
		_for (i, 0, m) an[i][i] = 1.0;
		while (b) {
			if (b & 1) an = an * a;
			a = a * a, b >>= 1;
		}
		return an;
	}

	inline void In () {
		n = rnt (), len = rnt (), alphabet = rnt ();
		_for (i, 1, n) {
			std::cin >> s[i];
			ac.Insert (s[i]);
		}
		return;
	}
	inline void Solve () {
		m = ac.Build (alphabet) + 1;
		MATRIX::Matrix ma = ac.GetMatrix (alphabet);
		ans.Init (m), ans[0][0] = 1.0;
		ma = FastPow (ma, len), ans = ans * ma;
		return;
	}
	inline void Out () {
		printf ("%.10Lf\n", ans[0][m]);
		return;
	}
}

\[\Huge{\mathfrak{The\ End}}
\]