「SHOI2014」概率充电器

题面

n <= 500000   0<= p,qi <= 100

题解

这是道概率树形DP题，但是很难推怎么用加法原理和乘法原理正向求每个点被充电的概率，所以我们求每个点不被充电的概率。

我们发现求不被充电的概率很好求。

dp[x][0] 表示x点不被x的子树（包括它自己）充电的概率，dp[x][1] 表示x点不被x的祖先充电的概率。

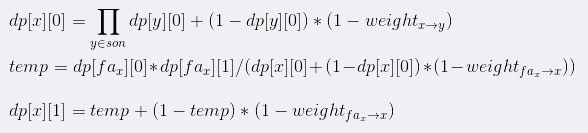
我们发现，这里面有除法，所以要判断是否为零，我们会发现，如果为零的话，那么dp[x][1]*dp[x][0]就肯定等于零，所以dp[x][1]可以取任意值，最后的答案也是对的。

CODE

#include<cstdio>
#include<iostream>
#include<cstring>
#include<vector>
#include<queue>
#include<stack>
#include<algorithm>
#define LL long long
#define MAXN 500005
using namespace std;
inline int read() {
	int f = 1,x = 0;char s = getchar();
	while(s < '0' || s > '9') {if(s == '-') f = -1;s = getchar();}
	while(s >= '0' && s <= '9') {x = x * 10 + s - '0';s = getchar();}
	return x * f;
}
struct ed{
	int v;
	double w;
	ed(){v = 0;w = 0.0;}
	ed(int V,double W){v = V;w = W;}
};
vector<ed> g[MAXN];
double dp[MAXN][2],a[MAXN];
int n,m,i,j,s,o,k,cnt;
void dfs(int x,int fa) {
	dp[x][0] = (1.0 - a[x]);
//	dp[x][0] = min(dp[x][0],1.0);
	for(int i = 0;i < g[x].size();i ++) {
		if(g[x][i].v != fa) {
			dfs(g[x][i].v,x);
			int y = g[x][i].v;
			double w = g[x][i].w;
			dp[x][0] *= (dp[y][0] + (1.0 - dp[y][0]) * (1.0 - w));
//			dp[x][0] = min(dp[x][0],1.0);
		}
	}
	return ;
}
void dfs2(int x,int fa,double edge) {
	double t = (dp[x][0] + (1.0 - dp[x][0]) * (1.0 - edge));
	if(t < 1e-6) t = 0;
	else t = dp[fa][1] * dp[fa][0] / t;
	dp[x][1] = t + (1.0 - t) * (1 - edge);
	if(fa == x) dp[x][1] = 1.0;
//	dp[x][0] = min(dp[x][0],1.0);
	for(int i = 0;i < g[x].size();i ++) {
		if(g[x][i].v != fa) {
			dfs2(g[x][i].v,x,g[x][i].w);
		}
	}
	return ;
}
int main() {
	n = read();
	for(int i = 1;i < n;i ++) {
		s = read();o = read();
		double p = read() / 100.0;
		g[s].push_back(ed(o,p));
		g[o].push_back(ed(s,p));
	}
	for(int i = 1;i <= n;i ++) {
		a[i] = read() / 100.0;
	}
	dfs(1,1);
	dfs2(1,1,0.0);
	double ans = 0.0;
	for(int i = 1;i <= n;i ++) {
		ans += (1.0 - dp[i][0]*dp[i][1]);
	}
	printf("%.6f\n",ans);
	return 0;
}