【美国血统 American Heritage 题解】已知前序中序 求后序

题目：

题目名称：美国血统 American Heritage

题目来源：美国血统 American Heritage

---

## 题目描述

农夫约翰非常认真地对待他的奶牛们的血统。然而他不是一个真正优秀的记帐员。他把他的奶牛

们的家谱作成二叉树，并且把二叉树以更线性的“树的中序遍历”和“树的前序遍历”的符号加以记录而 不是用图形的方法。

你的任务是在被给予奶牛家谱的“树中序遍历”和“树前序遍历”的符号后，创建奶牛家谱的“树的

后序遍历”的符号。每一头奶牛的姓名被译为一个唯一的字母。（你可能已经知道你可以在知道树的两

种遍历以后可以经常地重建这棵树。）显然，这里的树不会有多于 26 个的顶点。 这是在样例输入和 样例输出中的树的图形表达方式：

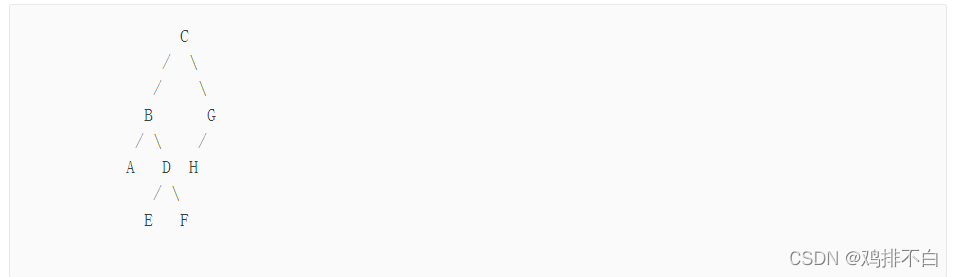
树的中序遍历是按照左子树，根，右子树的顺序访问节点。

树的前序遍历是按照根，左子树，右子树的顺序访问节点。

树的后序遍历是按照左子树，右子树，根的顺序访问节点。

输入格式 第一行： 树的中序遍历

第二行： 同样的树的前序遍历

输出格式 单独的一行表示该树的后序遍历。

输入输出样例

输入

ABEDFCHG

CBADEFGH

输出

AEFDBHGC

说明/提示

题目翻译来自NOCOW。

USACO Training Section 3.4

题解：

1、 题目分析

给出一个二叉树的前序和中序 ，求出后序

前序：CBADEFGH

中序：ABEDFCHG

首先从前序拿一个 到中序去寻找

现在拿Ｃ到中序里去寻找 ABEDF为Ｃ的左子树 ＨＧ为Ｃ的右子树

第二步　　　　拿Ｂ往中序里面找，Ａ为Ｂ的左子树　　ＥＤＦ右子树（右范围应在Ｂ～Ａ）

第三步 拿Ａ往中序　　　无左无右 即现在可以画出

			Ｃ
		/			＼
	Ｂ
／

Ａ

第四步 拿Ｄ往中序 左有Ｅ　右有Ｆ

第五步　拿Ｅ往中序 左无 右无

第六步　类似

按此规律能得轻松还原　　　树的图

转成后序　　使用递归即可

代码如下

#include <bits/stdc++.h>

using namespace std;

string pre, inor;		//前序  中序

void work(string pre, string inor)
{
	if (pre.empty())
		return;
	char root = pre[0];		//取前序序列的最前一个

	int k = inor.find(root);		//在中序里面去寻找   前序的数

	pre.erase(pre.begin());			//删除前序的第一个

	//从零开始切割   k个			即到k-1
	string leftpre = pre.substr(0, k);//表示从0取到k-1

	//从k+1到最后一个
	string rightpre = pre.substr(k);//表示从k取到最后

	string leftinor = inor.substr(0, k);
	string rightinor = inor.substr(k + 1);

	work(leftpre, leftinor);

	work(rightpre, rightinor);

	printf("%c", root);
}

int main()
{
	cin >> inor >> pre;
	work(pre, inor);
	return 0;
}

---