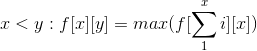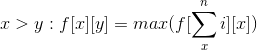弹簧高跷题解---双向DP---DD(XYX)的博客
三 . 弹簧高跷
时间限制: 1 Sec 内存限制: 128 MB
题目描述、输入、输出
-----------
方法
这道题用DP是可以解决的。因为每一次跳跃都与前一次跳跃有关,也就是说,每次要枚举前两次的跳跃落点,然后才能计算出某点到一个落点的最优解。这样一来,就可以定义一个 f [ ] [ ] ,f[ i ][ j ] 表示 以 “ 从 i 点跳到 j 点 ” 结束 的 一整次跳跃过程 中,得到的最高分 (注意: 可能是 i < j,也可能是 i > j,当然也有 i = j 的情况)。状态转移方程:
(分数)
先处理 f[ i ][ i ] 的情况,然后正逆序都进行一次三重循环。
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<queue>
#include<vector>
using namespace std;
void read(int &x) {
int f = 1;x = 0;char s = getchar();
while(s < '0' || s > '9') {if(s == '-')f = -1;s = getchar();}
while(s >= '0' && s <= '9') {x = x * 10 + s - '0';s = getchar();}
x *= f;
}
struct no{
int x,h;
}a[1005];
bool operator < (no a,no b) {
return a.x < b.x;
}
bool operator > (no a,no b) {
return b < a;
}
int n,m,s,o,i,j,k,ans = 0;
int dp[1005][1005];
int main() {
read(n);
for(i = 1;i <= n;i ++) {
read(a[i].x);read(a[i].h);
ans = max(ans,a[i].h);
}
sort(a + 1,a + 1 + n);
for(i = 1;i <= n;i ++) {
dp[i][i] = a[i].h;
for(j = 1;j < i;j ++) {
dp[j][i] = dp[j][j];
for(k = j - 1;k > 0 && a[j].x - a[k].x <= a[i].x - a[j].x;k --) {
dp[j][i] = max(dp[j][i],dp[k][j]);
}
dp[j][i] += a[i].h;
ans = max(ans,dp[j][i]);
}
}
for(i = n;i > 0;i --) {
for(j = n;j > i;j --) {
dp[j][i] = dp[j][j];
for(k = j + 1;k <= n && a[k].x - a[j].x <= a[j].x - a[i].x;k ++) {
dp[j][i] = max(dp[j][i],dp[k][j]);
}
dp[j][i] += a[i].h;
ans = max(ans,dp[j][i]);
}
}
printf("%d",ans);
return 0;
}
弹簧高跷题解---双向DP---DD(XYX)的博客的更多相关文章
- (四连测)滑雪场的高度差题解---二分 + 搜索---DD(XYX)的博客
滑雪场的高度差 时间限制: 1 Sec 内存限制: 128 MB 题目描述 滑雪场可以看成M x N的网格状山地(1 <= M,N <= 500),每个网格是一个近似的平面,具有水平高度 ...
- 圆形谷仓Circular Barn_Silver---(DP优化 / )队列 + 贪心(复杂度O(2n))---DD(XYX)的博客
目录 小数据 大数据 小数据 题目描述 农夫约翰有一个圆形的谷仓,谷仓分成了环形的n(3≤n≤1000)个房间,编号为1 , 2 , -- .每个房间有三个门,两个门通往两个相邻的房间,第三个门朝外. ...
- 拥挤的奶牛题解---队列优化DP---DD(XYX)的博客
拥挤的奶牛 时间限制: 1 Sec 内存限制: 128 MB 题目描述 FJ的n头奶牛(1<=n<=50000)在被放养在一维的牧场.第i头奶牛站在位置x(i),并且x(i)处有一个高度 ...
- 你有PSD的学位吗? - dp的日志 - 网易博客
你有PSD的学位吗? - dp的日志 - 网易博客 你有PSD的学位吗? 2011-08-01 12:58:40| 分类: 感悟 | 标签:自我提升 |字号 大中小 订阅 去年, ...
- 洛谷P2507 [SCOI2008]配对 题解(dp+贪心)
洛谷P2507 [SCOI2008]配对 题解(dp+贪心) 标签:题解 阅读体验:https://zybuluo.com/Junlier/note/1299251 链接题目地址:洛谷P2507 [S ...
- Blocks题解(区间dp)
Blocks题解 区间dp 阅读体验...https://zybuluo.com/Junlier/note/1289712 很好的一道区间dp的题目(别问我怎么想到的) dp状态 其实这个题最难的地方 ...
- POJ-2282题解&数位DP总结
一.题意 给定一个区间[a, b](注意输入的时候可能a > b,所以,在数据输入后,要先比较a和b,如果a > b,交换a和b的值),统计这个区间里面,数位上有多少个0.多少个1.--. ...
- HDU3085NightmareII题解--双向BFS
题目链接 http://acm.hdu.edu.cn/showproblem.php?pid=3085 分析 大意就是一个男孩和一个女孩在网格里,同时还有两个鬼,男孩每轮走三步,女孩每轮走一步,与鬼曼 ...
- HDU4507 吉哥系列故事——恨7不成妻 题解 数位DP
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=4507 题目大意: 找到区间 \([L,R]\) 范围内所有满足如下条件的数的 平方和 : 不包含'7' ...
随机推荐
- SCI论文写作注意事项
1. 先写结论:(划定范围,以防添加无效的内容) 并非一开始就把整个结论都写出来,而是把
- torch.nn.MSELoss()函数解读
转载自:https://www.cnblogs.com/tingtin/p/13902325.html
- 数位 dp 总结
数位 dp 总结 特征 问你一个区间 \([L,R]\) 中符合要求的数的个数 一个简单的 trick :把答案拆成前缀和 \(Ans(R)-Ans(L-1)\) 如何求 \(Ans()\) ,就要用 ...
- LVGL库入门教程01-移植到STM32(触摸屏)
LVGL库移植STM32 LVGL库简介 LVGL(Light and Versatile Graphics Library)是一个免费.开源的嵌入式图形库,可以创建丰富.美观的界面,具有许多可以自定 ...
- openssl客户端编程:一个不起眼的函数导致的SSL会话失败问题
我们目前大部分使用的openssl库还是基于TLS1.2协议的1.0.2版本系列,如果要支持更高的TLS1.3协议,就必须使用openssl的1.1.1版本或3.0版本.升级openssl库有可能会导 ...
- ssh-配置及使用
ssh配置文件 SSH的配置文件在/etc/ssh/目录下 openssh-client安装后,生成的配置文件为ssh_config,主要用于连接其他linux主机时,加载此文件 op ...
- idea如何实现Servlet接口
idea如何实现Servlet接口 project structure ---> Libraries ---> 点击加号+ ----> 找到安装tomcat的目录,再找lib下的se ...
- 学习C4C的视频分享
- 【一知半解】synchronied
synchronized是什么 synchronized是java同步锁,同一时刻多个线程对同一资源进行修改时,能够保证同一时刻只有一个线程获取到资源并对其进行修改,因此保证了线程安全性. synch ...
- 博客从 CloudBase 迁移至云主机
迁移起因 原来的博客 其实从很久以前就想要写博客,但总是断断续续的,一直都没有认真地开始. 最终,决定使用静态博客工具作为自己博客的承载体.在多种工具的比较下,最终选择了 Hugo 并部署到 Gith ...