（Good topic）圆圈中最后剩下的数字（leetcode 3.30每日打卡）

著名的约瑟夫问题：

0,1,,n-1这n个数字排成一个圆圈，从数字0开始，每次从这个圆圈里删除第m个数字。求出这个圆圈里剩下的最后一个数字。

例如，0、1、2、3、4这5个数字组成一个圆圈，从数字0开始每次删除第3个数字，则删除的前4个数字依次是2、0、4、1，因此最后剩下的数字是3。

 

示例 1：

输入: n = 5, m = 3
输出: 3

示例 2：

输入: n = 10, m = 17
输出: 2

 

限制：

 1 <= n <= 10^5
 1 <= m <= 10^6

 

 

 

1.一般的模拟

       超时，至于超时的原因，题解区有人解释了，单纯的模拟时间复杂度是O(mn),因为找到第m个数字，执行n-1次。预估一下运算时间，n<10^5，则O(n^2)的算法耗时是几秒，根据机器性能，也可能是十几秒，也可能一秒多，而这个题的规模是10^6,所以会超时。

 1 int Num[100000] = {0};
 2 int lastRemaining(int n, int m)  //n为规模 m为第m个数
 3 {
 4     int index = 0;  //作下标
 5     int i = 1;
 6     int counter = n;
 7
 8     for (int i = 0; i < n; i++)
 9     {
10         Num[i] = i;
11     }
12
13     while (counter > 1)
14     {
15         if (Num[index] != -1)
16         {
17             if (i == m)
18             {
19                 Num[index] = -1;
20                 counter--;
21             }
22
23             i++;
24
25             if (i > m)
26             {
27                 i = 1;
28             }
29         }
30
31         index++;
32         if (index >= n)
33         {
34             index = 0;
35         }
36     }
37     int lastNum;
38     for (i = 0; i < n; i++)
39     {
40         if (Num[i] != -1)
41         {
42             lastNum = Num[i];
43         }
44     }
45     return lastNum;
46 }

2.数学方法：leetcode甜姨的思路很明白，算法复杂度O(n).

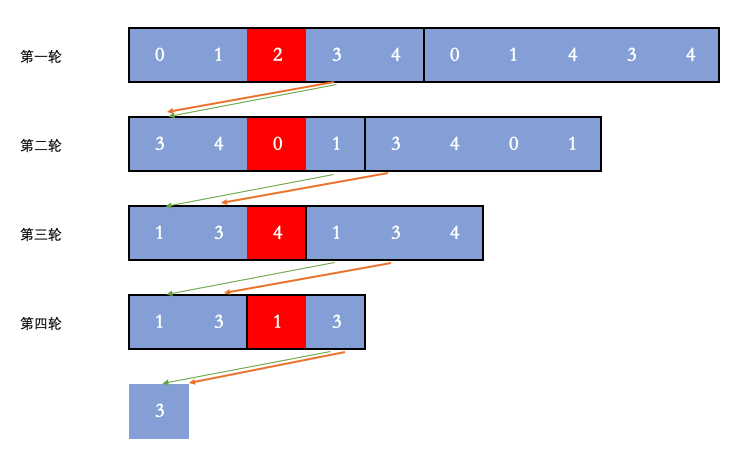
采用倒推的方式，找出最后所剩数字的下标。

我们可以反向推出这个数字在之前每个轮次的位置。
最后剩下的 3 的下标是 0。
第四轮反推，补上 mmm 个位置，然后模上当时的数组大小 222，位置是(0 + 3) % 2 = 1。
第三轮反推，补上 mmm 个位置，然后模上当时的数组大小 333，位置是(1 + 3) % 3 = 1。
第二轮反推，补上 mmm 个位置，然后模上当时的数组大小 444，位置是(1 + 3) % 4 = 0。
第一轮反推，补上 mmm 个位置，然后模上当时的数组大小 555，位置是(0 + 3) % 5 = 3。
所以最终剩下的数字的下标就是3。因为数组是从0开始的，所以最终的答案就是3

总结一下反推的过程，就是 (当前index + m) % 上一轮剩余数字的个数

作者：sweetieeyi
链接：https://leetcode-cn.com/problems/yuan-quan-zhong-zui-hou-sheng-xia-de-shu-zi-lcof/solution/javajie-jue-yue-se-fu-huan-wen-ti-gao-su-ni-wei-sh/

 1 int lastRemaining(int n, int m)  //n为规模 m为第m个数
 2 {
 3 int ans = 0;
 4
 5     for (int i = 2; i <= n; i++)
 6     {
 7         ans = (ans + m) % i;
 8     }
 9
10     return ans;
11 }

3.递归+数学：也是利用了数学的思想，不过没怎么看懂，递归算法效率会比迭代更低

1 int lastRemaining(int n, int m)  //n为规模 m为第m个数
2 {
3     if(n == 1)
4     return 0;
5     return (lastRemaining(n-1,m)+m)%n;
6 }