伸展树（Splay）详解

引入

在一条链中，二叉查找树的时间复杂度就会退化成 \(O(n)\)，这时我们就需要平衡树来解决这个问题。

\(Splay\)（伸展树）是平衡树的一种，它的每一步插入、查找和删除的平摊时间都是 \(O(\log n)\)，出于对编程复杂度和算法性能的考虑，这是 OI 中常用的算法。

性质

\(Splay\) 本质上还是对二叉查找树的优化。所以它也具备二叉查找树的性质，即左子树任意节点的值 \(<\) 根节点的值 \(<\) 右子树任意节点的值。

操作

数组含义

root	tot	fa[i]	ch[i][0]	ch[i][1]	val[i]	size[i]	cnt[i]
根节点编号	节点数量	父节点编号	左儿子编号	右儿子编号	节点权值	子树大小	节点权值出现次数

基本操作

maintain(x)：维护子树大小

void Splay::maintain(int x)
{
	size[x] = size[ch[x][0]] + size[ch[x][1]] + cnt[x];
	return ;
}

get(x)：查询该节点是其父亲节点的左子树还是右子树

bool Splay::get(int x)
{
	if( x == ch[fa[x]][1] )
		return 1;
	return 0;
}

clear(x)：清理该节点

void Splay::clear(int x)
{
	ch[x][0] = ch[x][1] = fa[x] = val[x] = size[x] = cnt[x] = 0;
	return ;
}

旋转

旋转操作实际上是让某一个节点上移一个位置。

旋转操作需要保证，二叉查找树的性质不会改变，节点维护的信息依然正确，\(root\) 必须指向旋转后的根节点。

若节点 x 是其父亲的左节点

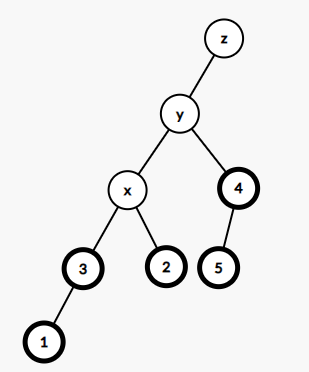
由于 \(x\) 的右儿子的权值大于 \(x\) 的权值，且 \(x\) 及其子树都属于 \(y\) 的左子树（即 \(x\) 的右子树实际上小于 \(y\) 的权值），所以我们将 \(x\) 的右子树改为 \(y\) 的左子树。

1. 将 \(x\) 的右儿子变成 \(y\) 的左儿子，如果 \(x\) 有右儿子的话就让它的父亲变成 \(y\)。
   
   ch[y][0] = ch[x][1]; fa[ch[x][1]] = y;

由于 \(y\) 及其子树的权值都大于 \(x\) 的权值，所以我们让 \(y\) 成为 \(x\) 的右儿子。

1. 使 \(y\) 成为 \(x\) 的右儿子，\(x\) 变为 \(y\) 的父亲。
   
   ch[x][chk^1] = y; fa[y] = x;

2. 如果 \(x\) 此时不是根节点，那么 \(x\) 将继承原先 \(y\) 作为 \(z\) 的儿子的位置（\(x\) 取代 \(y\) 成为 \(z\) 的左儿子或右儿子）。
   
   fa[x] = z; if(z) ch[z][y == ch[z][1]] = x;

由此我们得到了节点 \(x\) 上升一个位置的树，显然，这棵树仍然满足二叉搜索树的性质。

实现

void Splay::rotate(int x)
{
	int y = fa[x],z = fa[y],chk = get(x);

	ch[y][chk] = ch[x][chk ^ 1];

	if( ch[x][chk ^ 1] )
		fa[ch[x][chk ^ 1]] = y;
	ch[x][chk ^ 1] = y;

	fa[y] = x;
	fa[x] = z;

	if(z)
		ch[z][y == ch[z][1]] = x;

	maintain(y);
	// 要先维护 y 的子树大小
	// 因为现在 y 是 x 的儿子
	maintain(x);// 别忘了维护子树大小 

	return ;
}

代码中采用异或来实现左右不同旋转情况，当然我们可以写两个函数分别来实现左旋和右旋。

伸展

伸展操作是在保持伸展树性质的前提下，将节点 \(x\) 转移到根节点。在这个转移过程中，我们分为三种情况。

首先我们设节点 \(x\) 的父节点为节点 \(y\)，若节点 \(y\) 有父节点，其父节点为 \(z\)。

第一种情况：\(y\) 是根节点

• 若 \(x\) 是 \(y\) 的左儿子，我们进行一次右旋操作
  
  
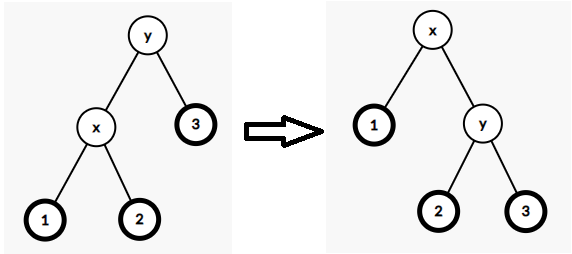
• 若 \(x\) 是 \(y\) 的右儿子，我们进行一次左旋操作

第二种情况：\(y\) 不是根节点，且 \(x\) 和 \(y\) 同为左儿子或右儿子

• 若 \(x\) 和 \(y\) 同时是各自父节点的左儿子，则进行两次右旋操作
• 若 \(x\) 和 \(y\) 同时是各自父节点的右儿子，则进行两次左旋操作

第三种情况：\(y\) 不是根节点，且 \(x\) 和 \(y\) 一个为左儿子一个为右儿子

• 若 \(x\) 是 \(y\) 的左儿子，\(y\) 是 \(z\) 的右儿子，则进行一次右旋 - 左旋操作
• 若 \(x\) 是 \(y\) 的右儿子，\(y\) 是 \(z\) 的左儿子，则进行一次左旋 - 右旋操作

实现

void Splay::splay(int x)
{
	for(int i = fa[x];i = fa[x],i; rotate(x))
		if( fa[i] )
		{
			if( get(x) == get(i) )
				rotate(i);
			else
				rotate(x);
		}

	root = x;

	return ;
}

插入

1. 如果树为空，则直接插入根节点

2. 如果找到了一个节点权值与插入权值相等，则增大该节点并维护信息，再进行 Splay 操作

3. 否则接着往下找，要是找到空节点就直接插入

实现

void Splay::insert(int v)
{
	if( root == 0 )
	{
		tot ++;
		val[tot] = v;
		cnt[tot] ++;
		root = tot;
		maintain(root);

		return ;
	}

	int cur = root,x = 0;
	while(1)
	{
		if( val[cur] == v )
		{
			cnt[cur] ++;
			maintain(cur);
			maintain(x);
			splay(cur);

			break;
		}
		x = cur;
		cur = ch[cur][val[cur] < v];

		if( cur == 0 )
		{
			tot ++;
			val[tot] = v;
			cnt[tot] ++;
			fa[tot] = x;
			ch[x][val[x] < v] = tot;

			maintain(tot);
			maintain(x);
			splay(tot);

			break;
		}
	}
}

寻找数 \(x\) 的排名（比它小的数的个数值 + 1）

1. 若 \(x\) 小于当前节点权值，则向左子树查找

2. 若 \(x\) 大于当前节点权值，则答案加上左子树大小 size[i] 和当前节点权值出现次数 cnt[i]

3. 若找到与 \(x\) 相等的节点，则返回当前答案 \(+ 1\)

实现

int Splay::find_rank(int v)
{
	int ans = 0,cur = root;
	while(1)
	{
		if( v < val[cur] )
			cur = ch[cur][0];
		else
		{
			ans += size[ch[cur][0]];
			if( v == val[cur] )
			{
				splay(cur);
				return ans + 1;
			}
			ans += cnt[cur];
			cur = ch[cur][1];
		}
	}
}

寻找排名为 \(x\) 的数的值

\(v\) 表示剩余排名，在初始排名的条件下不断减少。

1. 若左子树不为空且剩余排名 \(v\) 小于等于左子树大小 \(size\)（即 \(x\) 在左子树），向左子树查找

2. 否则减去左子树大小和根的出现次数作为剩余排名 \(v\)。若 \(v\leq 0\)，则返回根节点，否则向右子树查找。

实现

int Splay::find_num(int v)
{
	int cur = root;
	while(1)
	{
		if( ch[cur][0] != 0 && v <= size[ch[cur][0]] )
			cur = ch[cur][0];
		else
		{
			v -= cnt[cur] + size[ch[cur][0]];//.//
			if( v <= 0 )
			{
				splay(cur);
				return val[cur];
			}
			cur = ch[cur][1];
		}
	}
}

查询前驱（小于 \(x\) 的最大的数）

先插入节点 \(x\)，这样 \(x\) 就处在了根节点的位置。

此时 \(x\) 的左子树都小于 \(x\)，寻找 \(x\) 的左子树的最右边节点即小于 \(x\) 的最大的数。

实现

int Splay::pre()
{
	int cur = ch[root][0];
	if( cur == 0 )
		return cur;
	while( ch[cur][1] )
		cur = ch[cur][1];

	splay(cur);
	return cur;
}

查询后继（大于 \(x\) 的最小的数）

基本思想与查询前驱相同。

先插入节点 \(x\)，这样 \(x\) 就处在了根节点的位置。

此时 \(x\) 的右子树都大于 \(x\)，寻找 \(x\) 的右子树的最左边节点即大于 \(x\) 的最小的数。

实现

int Splay::next()
{
	int cur = ch[root][1];
	if( cur == 0 )
		return cur;
	while( ch[cur][0] )
		cur = ch[cur][0];

	splay(cur);
	return cur;
}

合并

对于合并两棵树，其中一棵树的值都小于另一棵树的值。

我们可以找到较小一棵树的最大值 \(x\)，将其旋转到根节点。

再把较大一棵树作为 \(x\) 的右子树插入。

删除

1. 首先将 \(x\) 转移到根节点

2. 若 \(x\) 值不只一个，即 \(cnt[x] > 1\)，则直接减一退出即可。

3. 否则将它的左右两棵子树合并

实现

void Splay::del(int v)
{
	find_rank(v);/////

	if( cnt[root] > 1 )
	{
		cnt[root] --;
		maintain(root);

		return ;
	}

	if( ch[root][0] == 0 && ch[root][1] == 0 )
	{
		clear(root);
		root = 0;
		return ;
	}

	if( ch[root][0] == 0 )
	{
		int cur = root;
		root = ch[root][1];
		fa[root] = 0;
		clear(cur);

		return ;
	}

	if( ch[root][1] == 0 )
	{
		int cur = root;
		root = ch[root][0];
		fa[root] = 0;
		clear(cur);

		return ;
	}

	int cur = root;
	int x = pre();
	fa[ch[cur][1]] = x;
	ch[x][1] = ch[cur][1];
	clear(cur);

	maintain(root);

	return ;
}

模板题

Luogu P3369 【模板】普通平衡树

完整代码

#include<bits/stdc++.h>

using namespace std;

const int MAXN = 114514; 

int n;

int root;
// 根节点
int ch[MAXN][2],fa[MAXN];
//  子节点( 0 左 1 右 )  父节点
int val[MAXN];
// 权值
int size[MAXN];
// 子树大小
int cnt[MAXN];
// 这个权值出现的次数
int tot;
// 节点个数  

struct Splay{
	void maintain(int x);
	// 维护子树大小
	bool get(int x);
	// 查找这个节点是父亲的左子树还是右子树
	void clear(int x);
	// 销毁这个节点
	void rotate(int x);
	// 旋转
	void splay(int x);
	// 伸展操作
	void insert(int v);
	// 插入数 v
	int find_rank(int v);
	// 查询数 v 的排名
	int find_num(int v);
	// 查询排名为 v 的数
	int pre();
	// 查询根节点的前驱
	int next();
	// 查询根节点的后继
	void del(int v);
	// 删除 v
}tree;

void Splay::maintain(int x)
{
	size[x] = size[ch[x][0]] + size[ch[x][1]] + cnt[x];
	return ;
}

bool Splay::get(int x)
{
	if( x == ch[fa[x]][1] )
		return 1;
	return 0;
}

void Splay::clear(int x)
{
	ch[x][0] = 0;
	ch[x][1] = 0;
	fa[x] = 0;
	val[x] = 0;
	size[x] = 0;
	cnt[x] = 0;

	return ;
}

void Splay::rotate(int x)
{
	int y = fa[x],z = fa[y],chk = get(x);

	ch[y][chk] = ch[x][chk ^ 1];

	if( ch[x][chk ^ 1] )
		fa[ch[x][chk ^ 1]] = y;
	ch[x][chk ^ 1] = y;

	fa[y] = x;
	fa[x] = z;

	if(z)
		ch[z][y == ch[z][1]] = x;

	maintain(y);
	maintain(x);

	return ;
}

void Splay::splay(int x)
{
	for(int i = fa[x];i = fa[x],i; rotate(x))
		if( fa[i] )
		{
			if( get(x) == get(i) )
				rotate(i);
			else
				rotate(x);
		}

	root = x;

	return ;
}

void Splay::insert(int v)
{
	if( root == 0 )
	{
		tot ++;
		val[tot] = v;
		cnt[tot] ++;
		root = tot;
		maintain(root);

		return ;
	}

	int cur = root,x = 0;
	while(1)
	{
		if( val[cur] == v )
		{
			cnt[cur] ++;
			maintain(cur);
			maintain(x);
			splay(cur);

			break;
		}
		x = cur;
		cur = ch[cur][val[cur] < v];

		if( cur == 0 )
		{
			tot ++;
			val[tot] = v;
			cnt[tot] ++;
			fa[tot] = x;
			ch[x][val[x] < v] = tot;

			maintain(tot);
			maintain(x);
			splay(tot);

			break;
		}
	}
}

int Splay::find_rank(int v)
{
	int ans = 0,cur = root;
	while(1)
	{
		if( v < val[cur] )
			cur = ch[cur][0];
		else
		{
			ans += size[ch[cur][0]];
			if( v == val[cur] )
			{
				splay(cur);
				return ans + 1;
			}
			ans += cnt[cur];
			cur = ch[cur][1];
		}
	}
}

int Splay::find_num(int v)
{
	int cur = root;
	while(1)
	{
		if( ch[cur][0] != 0 && v <= size[ch[cur][0]] )
			cur = ch[cur][0];
		else
		{
			v -= cnt[cur] + size[ch[cur][0]];//.//
			if( v <= 0 )
			{
				splay(cur);
				return val[cur];
			}
			cur = ch[cur][1];
		}
	}
}

int Splay::pre()
{
	int cur = ch[root][0];
	if( cur == 0 )
		return cur;
	while( ch[cur][1] )
		cur = ch[cur][1];

	splay(cur);
	return cur;
}

int Splay::next()
{
	int cur = ch[root][1];
	if( cur == 0 )
		return cur;
	while( ch[cur][0] )
		cur = ch[cur][0];

	splay(cur);
	return cur;
}

void Splay::del(int v)
{
	find_rank(v);/////

	if( cnt[root] > 1 )
	{
		cnt[root] --;
		maintain(root);

		return ;
	}

	if( ch[root][0] == 0 && ch[root][1] == 0 )
	{
		clear(root);
		root = 0;
		return ;
	}

	if( ch[root][0] == 0 )
	{
		int cur = root;
		root = ch[root][1];
		fa[root] = 0;
		clear(cur);

		return ;
	}

	if( ch[root][1] == 0 )
	{
		int cur = root;
		root = ch[root][0];
		fa[root] = 0;
		clear(cur);

		return ;
	}

	int cur = root;
	int x = pre();
	fa[ch[cur][1]] = x;
	ch[x][1] = ch[cur][1];
	clear(cur);

	maintain(root);

	return ;
}

int main()
{
	scanf("%d",&n);
	for(int i = 1,opt,x;i <= n; i++)
	{
		scanf("%d%d",&opt,&x);
		if( opt == 1 )
			tree.insert(x);
		else if( opt == 2 )
			tree.del(x);
		else if( opt == 3 )///
			printf("%d\n",tree.find_rank(x));
		else if( opt == 4 )////
			printf("%d\n",tree.find_num(x));
		else if( opt == 5 )
		{
			tree.insert(x);
			printf("%d\n",val[tree.pre()]);
			tree.del(x);
		}
		else
		{
			tree.insert(x);
			printf("%d\n",val[tree.next()]);
			tree.del(x);
		}
	}
	return 0;
}