CF1810D Candies题解

CF1810D Candies

点击查看原题

点击查看思路

经典的小学数学奥数题。

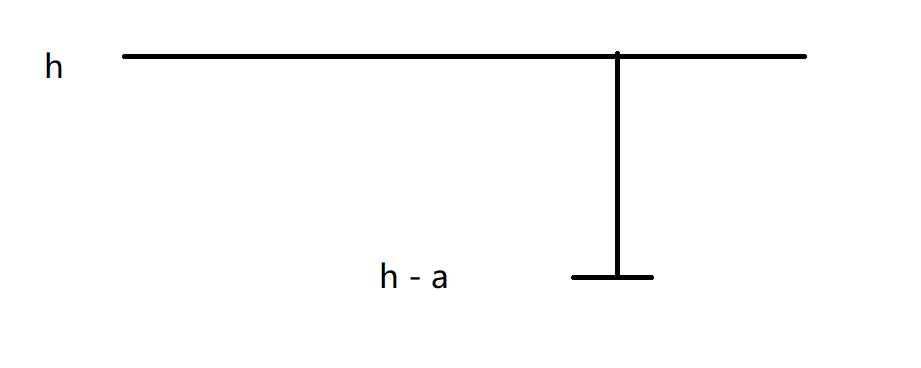
设 \(a\) 为每天往上爬的高度，\(b\) 为每天向下降的高度，\(n\) 为给定的需要爬上去的天数。

请注意，第 \(n\) 天爬上去了，就不会下降了。

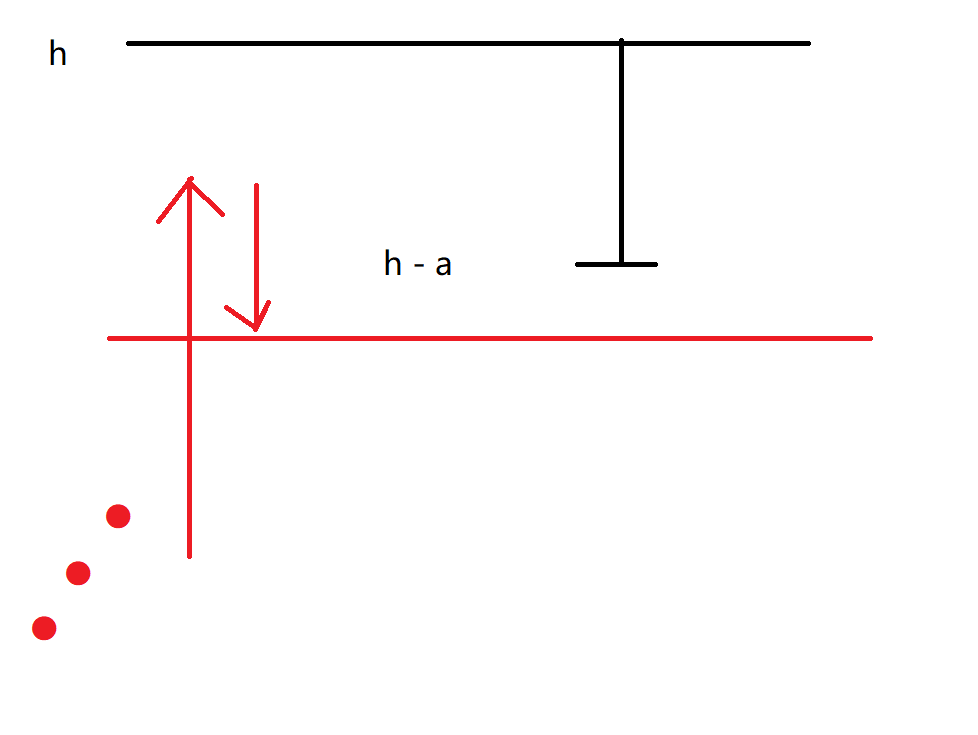
对于操作为 \(1\) 的，我们可以确定其范围。

因为要保证第 \(n\) 天就可以到达，且第 \(n - 1\) 天不能到达，所以其范围为标红部分：

用表达式表示为 \([(a - b) \times (n - 2) + a + 1, (a - b) \times (n - 1) + a]\)，其中 \((a - b) \times (n - 2) + a\) 为第 \(n - 1\) 天可以到达的最大高度 \(+1\) 才可以符合题意；\((a - b) \times (n - 1) + a\) 为第 \(n\) 天可以到达的最大高度。

需要特判 \(n = 1\) 的情况，此时其范围为 \([1, a]\)。

如果这个区间与之前之前计算的结果有交集，那么就是可以保留的，并更新区间，否则就丢弃之。

---

对于操作类型为 \(2\) 的，我们先计算出爬上 \(l\) 的高度需要的时间 \(t\)，计算方法如下。

假设高度为 \(h\)。

1. 首先要预留一个 \(a\)。

1. 然后计算 \(\left\lfloor\frac{h - a}{a - b}\right\rfloor\) 表示到达小于等于 \(h - a\) 的位置所需要的时间。

1. 如果刚好到达 \(h - a\) 的位置 \(+1\) 就可以了，否则 \(+2\)。

注意最好不要直接上取整，因为容易引起精度问题。

这样就计算出了 \(t\)，然后计算出花 \(t + 1\) 天爬上的高度范围是否与已知范围 \([l, r]\) 有交集，计算方法与前面的操作 \(1\) 类似，如果有那么证明不能准确获取其天数，输出 \(-1\)，否则输出天数。

注意我们不能直接判断已知范围 \(l\) 是否等于 \(r\)，因为有可能对于这一组询问在该区间内只有一种可能性，也是满足题意的。

点击查看代码

#include <bits/stdc++.h>

#define int long long

using namespace std;

bool check(int& l1, int& r1, int l2, int r2, bool flag) {
    int ll = max(l1, l2);
    int rr = min(r1, r2);
    if (ll > rr) return false;
    if (flag) {
        l1 = ll;
        r1 = rr;
    }
    return true;
}

void solve() {
    int q;
    cin >> q;
    int opt, a, b, c;
    int l = -1, r = 1e18;
    while (q--) {
        cin >> opt;
        if (opt == 1) {
            cin >> a >> b >> c;
            int lnew = -1, rnew = -1;
            if (c == 1) lnew = 1, rnew = a;
            else lnew = (a - b) * (c - 2) + a + 1, rnew = (a - b) * (c - 1) + a;
            if (check(l, r, lnew, rnew, true)) cout << "1 ";
            else cout << "0 ";
        }
        else {
            cin >> a >> b;
            int x = l, res = 0;
            if (a >= l) {
                res = 1;
            }
            else {
                x -= a;
                res = x / (a - b);
                x = res * (a - b);
                if (x == l - a) res++;
                else res += 2;
            }

            c = res + 1;
            int lnew = -1, rnew = -1;
            if (c == 1) lnew = 1, rnew = a;
            else lnew = (a - b) * (c - 2) + a + 1, rnew = (a - b) * (c - 1) + a;
            if (check(l, r, lnew, rnew, false)) res = -1;
            cout << res << ' ';
        }
    }
    cout << '\n';
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int T;
    cin >> T;
    while (T--) solve();
    return 0;
}