crypto常用工具

古典密码

维吉尼亚密码（Vigenere）：

https://github.com/atomcated/Vigenere（加密解密程序，包含自动猜测密钥功能）

https://www.guballa.de/vigenere-solver

whitespace语言：

https://ideone.com/

gmpy2

from gmpy2 import *

mpz(n)	#初始化一个大整数
mpfr(x)	# 初始化一个高精度浮点数x
d = invert(e,n) 	# 求逆元，de = 1 mod n
c = powmod(m,e,n)	# 幂取模，结果是 c = m^e mod n
is_prime(n)	 #素性检测
gcd(a,b)  	#欧几里得算法，最大公约数
gcdext(a,b)  	#扩展欧几里得算法
iroot(x,n) 	#x开n次根

sympy

from sympy import *

prime(n)  #第n个素数
isprime(n)  #素性检测
primepi(n)  #小于n的素数的总数
nextprime(n)  #下一个素数
prevprime(n)  #上一个素数
nthroot_mod(c,e,p,all_roots=True)  #有限域开方

Sage

定义

R.<X> = PolynomialRing(Zmod(n))
#Zmod(n):指定模，定义界限为n的环；Z表示整数；指定模是划定这个环的界限，就是有效的数字只有从0到n，其他的都通过与n取模来保证在0～n这个范围内；Zmod代表这是一个整数域中的n模环
#ZZ：整数环；QQ：有理数环；RR：实数环；CC：复数环
#R：只是一个指针，指向用polynomialring指定的那个环（可以使用任意字符）
#PolynomialRing：这个就是说建立多项式环
#.<X>：指定一个变量的意思（可以用任意字符）

数论

prime_pi(n)  #小于等于n的素数个数
divisors(n)  #n的因子
number_of_divisors(n)  #n的因子数
factor(n)  #n的因式分解
euler_phi(n)  #n的欧拉函数值
two_squares(n)   #n的两数平方组合
three_squares(n)  #n的三数平方组合
four_squares(n)  #n的四数平方组合

x.nth_root(n, truncate_mode=True) #x开n次方（不管是否完全开方，取整）
mod(x,p).nth_root(n) #x有限域开n次方

# x有限域开n次方，e大
def mod_nth_root(x, e, n):
    r, z = pari(f"r = sqrtn(Mod({x}, {n}), {e}, &z); [lift(r), lift(z)]")
    r, z = int(r), int(z)
    roots = [r]
    t = r
    while (t := (t*z) % n) != r:
        roots.append(t)
    return roots

多项式

f.subs({x:x1}) #把x1值代入x
f.univariate_polynomial() #映射为单变量多项式
f.univariate_polynomial().roots() #单变量多项式求根
f.coefficients() #多项式系数列表
f.padded_list(n) #多项式系数转换为长度为n的列表
f.list() #多项式系数
f.monic() #首一多项式
f.sub(x,x-1) #将x-1代入x
f.factor() #分解因式

#因式分解（单元）
x = PolynomialRing(RationalField(), 'x').gen()
f = (x^3 - 1)^2-(x^2-1)^2
f.factor()

#因式分解（二元）
x, y = PolynomialRing(RationalField(), 2, ['x','y']).gens()
f =  (9*y^6 - 9*x^2*y^5 - 18*x^3*y^4 - 9*x^5*y^4 + 9*x^6*y^2 + 9*x^7*y^3 + 18*x^8*y^2 - 9*x^11)
f.factor()

#GCD（单元）
x = PolynomialRing(RationalField(), 'x').gen()
f = 3*x^3 + x
g = 9*x*(x+1)
f.gcd(g)

#GCD（多元）
R.<x,y,z> = PolynomialRing(RationalField(), order='lex')
f = 3*x^2*(x+y)
g = 9*x*(y^2 - x^2)
f.gcd(g)

#多项式/整数转换
PR = PolynomialRing(GF(2),'x')
R.<x> = GF(2^2049)
pc = R.fetch_int(xx) #整数转多项式
xx = R(PR(pc)).integer_representation() #多项式转整数

矩阵

A = matrix(ZZ, [[1,1],[0,4]])
A.nrows() #行数
A.ncols() #列数
A.transpose() #转置
A.inverse() 或 A^(-1) #逆
A.rank() #秩
A.det() #行列式
A.stack(vector([1,2])) #矩阵后添加一行
A.augment(vector([1,2])) #矩阵后添加一列
A.insert_row(1, vector([1,2])) #在第一行插入
A.change_ring(QQ) #更换环为QQ
A.solve_left(B) 或 A/B #求解XA=B
A.solve_right(B) 或 A\B #求解AX=B
A.left_kernel() #求解XA=0，线性相关的行向量
A.right_kernel() #求解AX=0，线性相关的行向量
A.LLL() #最短正交基
A.multiplicative_order() #乘法阶

matrix.zero(2,3) / zero_matrix(2,3) #2*3零矩阵
matrix.identity(2) / identity_matrix(2) #2*2单位阵
block_matrix(QQ,[[A,zero_matrix(n,1)],[matrix(b),matrix([1e-16])]]) #矩阵拼接

解方程

var('x y')
solve([x+y==10,x*y==21],[x,y])

解线性方程组

AX = B

A = Matrix([[1,2,3],[3,2,1],[1,1,1]])
Y = vector([0,-4,-1])
X = A.solve_right(Y)
#或
A \ Y
#反斜杠 \ 可以代替 solve_right; 用 A \ Y 代替 A.solve right(Y).

求逆元

d = inverse_mod(e,fn) # sage求逆元

扩展欧几里得算法

d,u,v=xgcd(20,30)
print("d:{0} u:{1} v:{2}".format(d,u,v)) #d:10 u:-1 v:1

CRT（中国剩余定理）

crt([2,3,2],[3,5,7])

#仅适用模两两互素
def chinese_remainder(modulus, remainders):
    Sum = 0
    prod = reduce(lambda a, b: a*b, modulus)
    for m_i, r_i in zip(modulus, remainders):
        p = prod // m_i
        Sum += r_i * (inverse_mod(p,m_i)*p)
    return Sum % prod
chinese_remainder([3,5,7],[2,3,2]) #23

离散对数

#n为合数（Pohlig-Hellman）
x = discrete_log(mod(b,n),mod(a,n)) 

#n为质数或质数幂（线性筛Index Calculus）
R = Integers(99)
a = R(4)
b = a^9
b.log(a)

x = int(pari(f"znlog({int(b)},Mod({int(a)},{int(n)}))"))
x = gp.znlog(b, gp.Mod(a, n))

欧拉函数

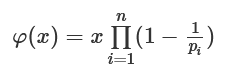
print(euler_phi(71)) #70

整数域椭圆曲线

#素数域
F = GF(7)
#素数域的阶
print(F.order())
#椭圆曲线E7(2,3)
E = EllipticCurve(F,[0,0,0,2,3])
#基点坐标
G = E.gens()[0]
#阶（不同的离散的点个数）
q = E.order()
#所有的点
allPoints = E.points()
#创建点
P = E(2,1)
#点的xy坐标值
P.xy()

#倍数点
Q = k*P
Q.division_points(k) # 结果为P

曲线

# 查亏格（Genus）
x, y = ZZ['x, y'].gens()
eq = x ^ 3 + y ^ 3 + 1 - d * x * y
Curve(eq).genus() # Genus=1为椭圆曲线

# 映射
# solve x^3+y^3+z^3=d*x*y*z
R.<xx,yy,zz> = Zmod(p)[]
cubic = xx^3 + yy^3 + zz^3 - d * xx * yy * zz
EC = EllipticCurve_from_cubic(cubic, morphism=False) #映射的椭圆曲线
mf = EllipticCurve_from_cubic(cubic, morphism=True) #映射关系
P =
PP = mf(P)

解模方程

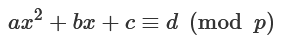
P.<x> = PolynomialRing(Zmod(p))
f = a * x^2 + b * x + c - d
x = f.monic().roots()
print(x)

解方程组

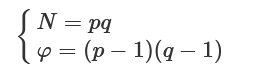
P.<p, q> = PolynomialRing(ZZ)
def solve(f1, f2):
	g = f1.resultant(f2, q)
	roots = g.univariate_polynomial().roots()
	if len(roots) == 0:
		return False
	p_ = abs(roots[0][0])
	q_ = abs(roots[1][0])
	return (min(p_, q_), max(p_, q_))

N =
phi =
f1 = (N + 1) - phi - p - q
f2 = N - p*q
p, q = solve(f1, f2)
(p, q)

参考：

https://jayxv.github.io/2020/05/20/sage%E5%B8%B8%E7%94%A8%E5%91%BD%E4%BB%A4/

结式

from sage.matrix.matrix2 import Matrix
def resultant(f1, f2, var):
    return Matrix.determinant(f1.sylvester_matrix(f2, var))

n =
P.<k,t2,t3,d> = PolynomialRing(Integers(n))
f1 = s1*k - h - r*d
f2 = s2*(k+t2) - h - r*d
f3 = s3*(k+t3) - h - r*d
h1 = resultant(f1, f2, d)
h2 = resultant(f1, f3, d)
g1 = resultant(h1, h2, k)
roots = g1.univariate_polynomial().roots()

WolframAlpha

https://www.wolframalpha.com/