【若归】背包dp做题笔记
前言:
现在决定未来,未来与过去无关。--波波
前置知识:
dd_engi的背包九讲(新版转载)
|
背包九讲——全篇详细理解与代码实现
背包问题 (附单调队列优化多重背包
|
背包问题入门(单调队列优化多重背包
题目来自学校OJ、洛谷、ybtOJ。

学校OJ:
A.采药
01背包(后面解题过程大部分均由01背包变形)板子题,加上一个滚动数组优化,没什么好说的。
$ 1<=i<=m,t>=j>=w[i]$
$f[j]=max(f[j],f[j-w[i]]+c[i]) $
#include<bits/stdc++.h>
using namespace std;
int w[10001],c[10001],f[10001];
int main()
{
int t,m,i,j;
cin>>t>>m;
for(i=1;i<=m;i++)
{
cin>>w[i]>>c[i];
}
for(i=1;i<=m;i++)
{
for(j=t;j>=w[i];j--)
{
f[j]=max(f[j],f[j-w[i]]+c[i]);
}
}
cout<<f[t]<<endl;
return 0;
}
B.开心的金明
与A类似,还是01背包板子,设第\(j\)件物品的价格为\(v[j]\),重要度为\(w[j]\),则第\(j\)件物品的价值为\(v[j]*w[j](j<=n)\)。
$ 1<=i<=m,n>=j>=v[i]$
$f[j]=max(f[j],f[j-v[i]]+p[i]) $
#include<bits/stdc++.h>
using namespace std;
int v[750001],p[750001],f[750001];
int main()
{
int n,m,i,j;
cin>>n>>m;
for(i=1;i<=m;i++)
{
cin>>v[i]>>p[i];
p[i]*=v[i];
}
for(i=1;i<=m;i++)
{
for(j=n;j>=v[i];j--)
{
f[j]=max(f[j],f[j-v[i]]+p[i]);
}
}
cout<<f[n]<<endl;
return 0;
}
C. 完全背包问题
完全背包板子(优化后面讲),因范围较小,选用不加优化的做法。
完全背包板子和和01背包板子仅有j的循环次序不同(注意一下,不要混淆),同时注意一下输出格式。
$ 1<=i<=n,w[i]<=j<=m$
$f[j]=max(f[j-w[i]]+c[i],f[j]) $
#include<bits/stdc++.h>
using namespace std;
int n,m,i,j,c[31],w[31],f[2001];
int main()
{
cin>>m>>n;
for(i=1;i<=n;i++)
{
cin>>w[i]>>c[i];
}
for(i=1;i<=n;i++)
{
for(j=w[i];j<=m;j++)
{
f[j]=max(f[j-w[i]]+c[i],f[j]);
}
}
cout<<"max="<<f[m];
return 0;
}
D.竞赛总分
P2722 [USACO3.1]总分 Score Inflation
完全背包板子(同C),加强一下印象。
$ 1<=i<=n,w[i]<=j<=m$
$f[j]=max(f[j-w[i]]+c[i],f[j]) $
#include<bits/stdc++.h>
using namespace std;
int c[10001],w[10001],f[10001];
int main()
{
int n,m,i,j;
cin>>m>>n;
for(i=1;i<=n;i++)
{
cin>>c[i]>>w[i];
}
for(i=1;i<=n;i++)
{
for(j=w[i];j<=m;j++)
{
f[j]=max(f[j-w[i]]+c[i],f[j]);
}
}
cout<<f[m];
return 0;
}
E.砝码称重
考虑两种解法,一种是暴力(时间复杂度为各砝码数量相乘),一种是背包dp(最坏情况下为\(6*1000^2\));记得初始化,注意输出格式。
暴力:
建议不要采用这种方式,或者加上特判(未写);如果是极限数据,就会被卡
#11
样例输入:65 34 34 23 23 21
样例输出:1000
#include<bits/stdc++.h>
using namespace std;
int c[1001];
int main()
{
int a[7],b[7],i,sum,ans=0;
cin>>a[1]>>a[2]>>a[3]>>a[4]>>a[5]>>a[6];
for(b[1]=0;b[1]<=a[1];b[1]++)
{
for(b[2]=0;b[2]<=a[2];b[2]++)
{
for(b[3]=0;b[3]<=a[3];b[3]++)
{
for(b[4]=0;b[4]<=a[4];b[4]++)
{
for(b[5]=0;b[5]<=a[5];b[5]++)
{
for(b[6]=0;b[6]<=a[6];b[6]++)
{
sum=b[1]+b[2]*2+b[3]*3+b[4]*5+b[5]*10+b[6]*20;
if(c[sum]==0)
{
c[sum]=1;
ans++;
}
}
}
}
}
}
}
ans--;
cout<<"Total="<<ans;
return 0;
}
背包dp:
思路是枚举每个砝码数量,若\(f[k]\)存在,则\(f[k+b[i]]\)一定存在;如果数据范围较大,可将f数组的类型从int改为bool。
#include<bits/stdc++.h>
using namespace std;
int a[7],b[7]={0,1,2,3,5,10,20},f[1001];
int main()
{
int i,j,k,ans=0;
for(i=1;i<=6;i++)
{
cin>>a[i];
}
f[0]=1;
for(i=1;i<=6;i++)
{
for(j=1;j<=a[i];j++)
{
for(k=1000;k>=0;k--)
{
if(f[k]==1)
{
if(f[k+b[i]]==0)
{
f[k+b[i]]=1;
ans++;
}
}
}
}
}
cout<<"Total="<<ans;
return 0;
}
F.最小乘车费用
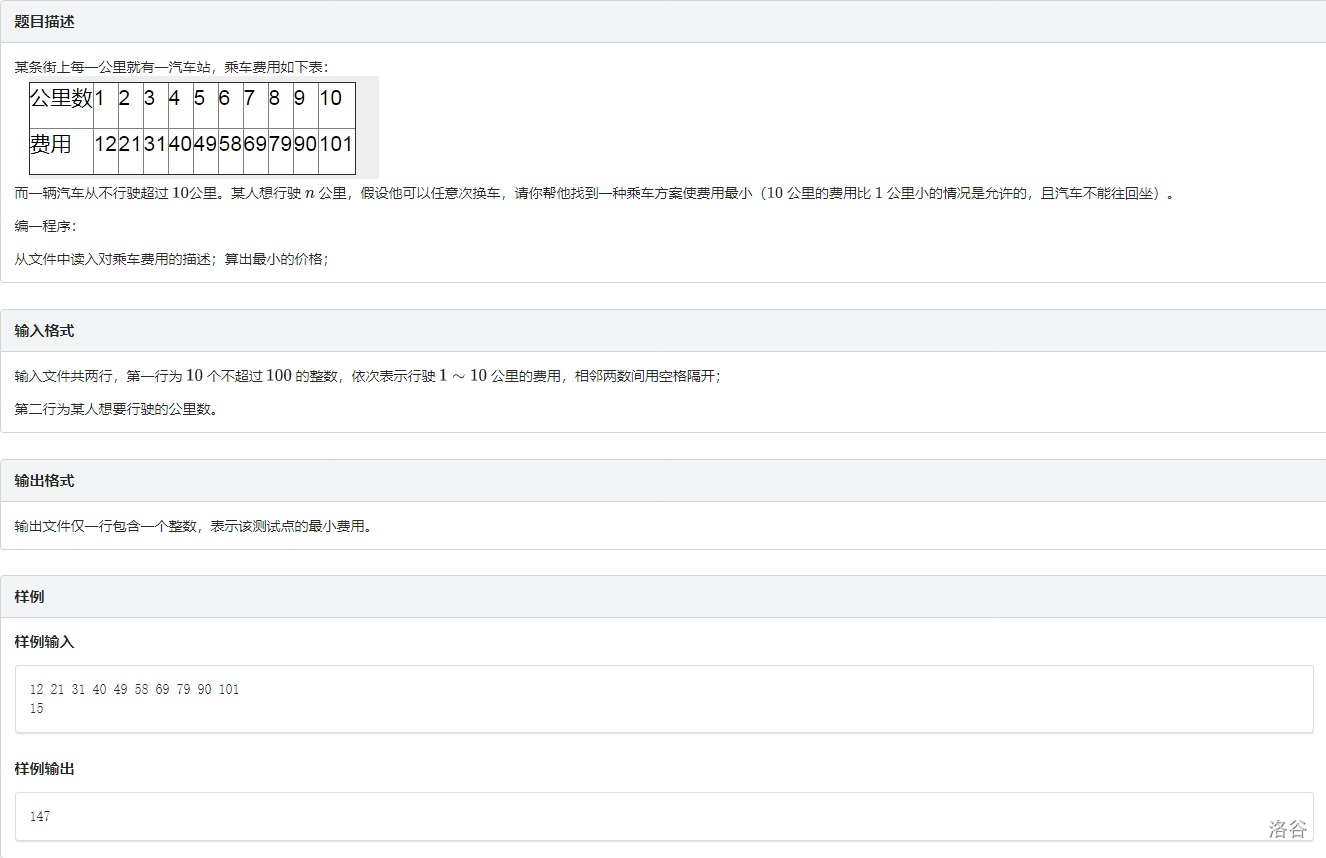
完全背包变形,枚举每种情况下的距离以达到状态转移。
$ 1<=i<=10,i<=j<=n$
$ f[j]=min(f[j-i]+w[i],f[j])$
#include<bits/stdc++.h>
using namespace std;
int f[10001],w[11];
int main()
{
int n,i,j;
memset(f,0x3f3f3f3f,sizeof(f));
f[0]=0;
for(i=1;i<=10;i++)
{
cin>>w[i];
}
cin>>n;
for(i=1;i<=10;i++)
{
for(j=i;j<=n;j++)
{
f[j]=min(f[j-i]+w[i],f[j]);//用f[j-i]+w[i]和f[j]取最小值更新f[j].f[j-i]表示到j-i的最短花费,加上w[i]即可(走i公里需要的花费)。
}
}
cout<<f[n];
return 0;
}
G.逃亡的准备
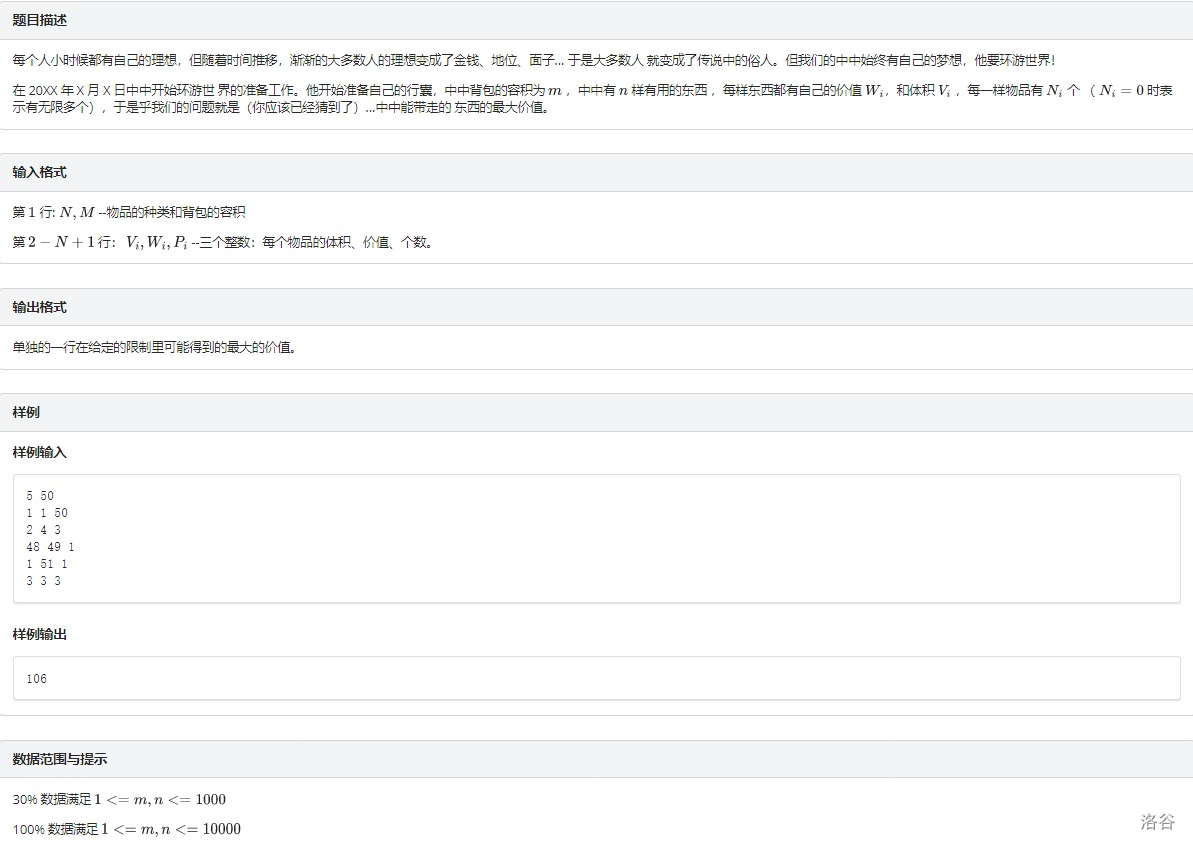
初看到这道题以为是混合背包板子,然后就TLE了。(小声bb:我还以为是测评姬波动,前前后后交了170+次)
后来考2022CSP前,将混合背包的01背包和多重背包进行了二进制优化,于是AC。(如果数据再ex亿点,可能要用单调队列优化)
\(1<=i<=n\)
\(if(p[i]==0)\) $ v[i]<=j<=m$ \(f[j]=max(f[j],f[j-v[i]]+w[i])\)
\(else\) 详见代码
#include <bits/stdc++.h>
using namespace std;
int f[10001],v[10001],w[10001],p[10001];
int main()
{
int n,m,i,j,k;
cin>>n>>m;
for(i=1;i<=n;i++)
{
cin>>v[i]>>w[i]>>p[i];
if(p[i]==0)//完全背包
{
for(j=v[i];j<=m;j++)
{
f[j]=max(f[j],f[j-v[i]]+w[i]);
}
}
else//01背包可以当作多重背包来处理
{
for(k=1;k<=p[i];k*=2)
{
for(j=m;j>=k*v[i];j--)
{
f[j]=max(f[j],f[j-k*v[i]]+k*w[i]);
}
p[i]-=k;
}
if(p[i]>0)
{
for(j=m;j>=p[i]*v[i];j--)
{
f[j]=max(f[j],f[j-p[i]*v[i]]+p[i]*w[i]);
}
}
}
}
cout<<f[m]<<endl;
return 0;
}
H.庆功会
不加优化的多重背包即可,优化详见G。
\(1<=i<=n,m>=j>=0,0<=k<=num[i]\)
$ if(j-k*w[i]>=0)$ \(f[j]=max(f[j],f[j-k*w[i]]+k*c[i])\)
#include<bits/stdc++.h>
using namespace std;
int w[10001],c[10001],num[10001],f[10001];
int main()
{
int m,n,i,j,k;
cin>>n>>m;
for(i=1;i<=n;i++)
{
cin>>w[i]>>c[i]>>num[i];
}
for(i=1;i<=n;i++)
{
for(j=m;j>=0;j--)
{
for(k=0;k<=num[i];k++)
{
if(j-k*w[i]>=0)//很重要,避免RE
{
f[j]=max(f[j],f[j-k*w[i]]+k*c[i]);
}
}
}
}
cout<<f[m]<<endl;
return 0;
}
I.混合背包
不加优化的混合背包即可,优化详见G。
\(1<=i<=n\)
\(if(num[i]==1)\) $ m>=j>=w[j]$ \(f[j]=max(f[j],f[j-w[i]]+c[i])\)
\(if(num[i]==0)\) $ w[i]<=j<=m$ \(f[j]=max(f[j],f[j-w[i]]+c[i])\)
\(if(num[i]>1)\) \(m>=j>=0,0<=k<=num[i]\) \(if(j-k*w[i]>=0)\) \(f[j]=max(f[j],f[j-k*w[i]]+k*c[i])\)
#include<bits/stdc++.h>
using namespace std;
int w[10001],c[10001],num[10001],f[10001];
int main()
{
int m,n,i,j,k;
cin>>m>>n;
for(i=1;i<=n;i++)
{
cin>>w[i]>>c[i]>>num[i];
}
for(i=1;i<=n;i++)
{
if(num[i]==1)
{
for(j=m;j>=w[i];j--)
{
f[j]=max(f[j],f[j-w[i]]+c[i]);
}
}
else
{
if(num[i]==0)
{
for(j=w[i];j<=m;j++)
{
f[j]=max(f[j],f[j-w[i]]+c[i]);
}
}
else
{
for(j=m;j>=0;j--)
{
for(k=0;k<=num[i];k++)
{
if(j-k*w[i]>=0)
{
f[j]=max(f[j],f[j-k*w[i]]+k*c[i]);
}
}
}
}
}
}
cout<<f[m]<<endl;
return 0;
}
J.NASA的食物计划
二维费用的背包板子。(教练说非常简单)
\(1<=i<=q,p>=j>=w[i],q>=k>=v[i]\) \(f[j][k]=max(f[j][k],f[j-w[i]][k-v[i]]+c[i])\)
#include<bits/stdc++.h>
using namespace std;
int w[401],v[401],c[401],f[401][401];
int main()
{
int p,q,n,i,j,k;
cin>>p>>q>>n;
for(i=1;i<=n;i++)
{
cin>>w[i]>>v[i]>>c[i];
}
for(i=1;i<=q;i++)
{
for(j=p;j>=w[i];j--)
{
for(k=q;k>=v[i];k--)
{
f[j][k]=max(f[j][k],f[j-w[i]][k-v[i]]+c[i]);
}
}
}
cout<<f[p][q];
return 0;
}
K. 分组背包
分组背包板子。
每组物品有若干种策略:选本组的某一件,或者一件也不选。即设 \(f[k][j]\) 表示前 \(k\) 组物品花费费用 \(j\) 能取得的最大权值,则有$ f[k][j]=max(f[k-1][j],f[k-1][j-w[i]+c[i]|物品i属于第k组)$。接着将其用滚动数组优化即可(转换为一维数组)。
\(1<=k<=t,v>=j>=0,1<=i<=group[k][0]\)
\(if(j>=w[group[i][k]]) f[j]=max(f[j],f[j-w[group[i][k]]]+c[group[i][k]])\)
#include<bits/stdc++.h>
using namespace std;
int group[1001][1001],w[1001],c[1001],f[1001];
int main()
{
int v,n,t,i,j,k,p,q;
cin>>v>>n>>t;
for(i=1;i<=n;i++)
{
cin>>w[i]>>c[i]>>p;
group[p][0]++;
group[p][group[p][0]]=i;
}
for(i=1;i<=t;i++)
{
for(j=v;j>=0;j--)
{
for(k=1;k<=group[i][0];k++)
{
q=group[i][k];
if(j>=w[q])
{
f[j]=max(f[j],f[j-w[q]]+c[q]);
}
}
}
}
cout<<f[v]<<endl;
return 0;
}
L.新年趣事之打牌
01背包的变形,判断是否有解及多组解,同时进行记录,方便后面输出。
#include<bits/stdc++.h>
using namespace std;
int w[100001],s[100001],f[100001],ans[100001];
int main()
{
int n,num,i,j,sum;
cin>>num>>n;
for(i=1;i<=n;i++)
{
cin>>w[i];
}
s[0]=1;//初始化
for(i=1;i<=n;i++)//01背包
{
for(j=num;j>=w[i];j--)
{
if(s[j-w[i]]!=0)
{
s[j]+=s[j-w[i]];
if(f[j]==0)
{
f[j]=i;//初始化+记录路径
}
}
}
}
if(s[num]==0)//无解
{
cout<<"0";
}
if(s[num]==1)//有解
{
sum=num;
while(sum>0)//记录路径(纸牌)
{
ans[f[sum]]=1;
sum-=w[f[sum]];
}
for(i=1;i<=n;++i)//输出
{
if(ans[i]==0)
{
cout<<i<<" ";
}
}
}
if(s[num]>1)//有多组解
{
cout<<"-1";
}
return 0;
}
M. 积木城堡
01背包变形,判断是否有解。
#include<bits/stdc++.h>
using namespace std;
int h[10001],num[10001],f[10001];
int main()
{
int n,ans=0x3f3f3f3f,sum,i,j,k,p,flag=0;//初始化
cin>>n;
for(i=1;i<=n;i++)
{
memset(f,0,sizeof(f));//每次循环都要清空
memset(h,0,sizeof(h));//每次循环都要清空(这条语句可要可不要,但还是带上的好)
f[0]=1;//初始化
p=1;
sum=0;
while(cin>>h[p])
{
if(h[p]==-1)
{
break;
}
else
{
sum+=h[p];
}
p++;
}
p--;//因为读入结束后,p会比实际长度多1,故p--
ans=min(ans,sum);//ans为查询的最大值
for(j=1;j<=p;j++)//01背包
{
for(k=sum;k>=h[j];k--)
{
if(f[k-h[j]]==1)
{
f[k]=1;
}
}
}
for(j=sum;j>=1;j--)//标记下
{
if(f[j]==1)
{
num[j]++;
}
}
}
for(i=ans;i>=1;i--)
{
if(num[i]==n)//有解
{
cout<<i;
flag=1;
break;
}
}
if(flag==0)//无解
{
cout<<"0";
}
return 0;
}

洛谷:
注意数据范围有亿点大,不能用正常的01背包解决。换一种方式,让f数组用来储存容量,即\(f[i]\)用来储存价值为 \(i\) 时所需的最小容量。
$ 1<=i<=t,1000*t>=j>=c[i]$
\(f[j]=max(f[j],f[j-c[i]]+w[i])\)
#include<bits/stdc++.h>
using namespace std;
int w[1000001],c[1000001],f[1000001];
int main()
{
int t,m,i,j;
cin>>t>>m;
memset(f,0x3f,sizeof(f));
for(i=1;i<=t;i++)
{
cin>>w[i]>>c[i];
}
f[0]=0;
for(i=1;i<=t;i++)
{
for(j=1000*t;j>=c[i];j--)
{
f[j]=min(f[j],f[j-c[i]]+w[i]);
}
}
for(i=1000*t;i>0;i--)
{
if(f[i]<=m)
{
cout<<i;
break;
}
}
return 0;
}
单调队列优化多重背包板子
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
int f[100001],g[100001],w[100001],v[100001],p[100001];
int main()
{
int n,m,i,j,k;
cin>>n>>m;
for(i=1;i<=n;i++)
{
cin>>v[i]>>w[i]>>p[i];
if(p[i]==0)
{
for(j=w[i];j<=m;j++)
{
f[j]=max(f[j],f[j-w[i]]+v[i]);
}
}
else
{
memcpy(g,f,sizeof(f));
for(j=0;j<w[i];j++)
{
deque<int>q;
for(k=0;k<=(m-j)/w[i];k++)
{
if(q.empty()==0&&q.front()<k-p[i])
{
q.pop_front();
}
while(q.empty()==0&&g[j+q.back()*w[i]]-q.back()*v[i]<=g[j+k*w[i]]-k*v[i])
{
q.pop_back();
}
q.push_back(k);
f[j+k*w[i]]=g[j+q.front()*w[i]]+(k-q.front())*v[i];
}
}
}
}
cout<<f[m]<<endl;
return 0;
}
/*
#include <bits/stdc++.h>
using namespace std;
int f[100001],w[100001],v[100001],p[100001];
int main()
{
int n,m,i,j,k;
cin>>n>>m;
for(i=1;i<=n;i++)
{
cin>>v[i]>>w[i]>>p[i];
if(p[i]==0)
{
for(j=w[i];j<=m;j++)
{
f[j]=max(f[j],f[j-w[i]]+v[i]);
}
}
else
{
for(k=1;k<=p[i];k*=2)
{
for(j=m;j>=k*w[i];j--)
{
f[j]=max(f[j],f[j-k*w[i]]+k*v[i]);
}
p[i]-=k;
}
if(p[i]>0)
{
for(j=m;j>=p[i]*w[i];j--)
{
f[j]=max(f[j],f[j-p[i]*w[i]]+p[i]*v[i]);
}
}
}
}
cout<<f[m]<<endl;
return 0;
}
*/
【若归】背包dp做题笔记的更多相关文章
- 状压dp做题笔记
CodeChef Factorial to Square (分块决策) Description 给定一个n,要求在[1,n]中删除一些数,并使剩下的数的乘积是一个完全平方数,同时要求乘积最大,求删除方 ...
- 计数dp做题笔记
YCJS 3924 饼干 Description 给定一个长度为\(n\)的序列,序列每个元素的取值为\([1,x]\),现在给定\(q\)个区间,求在所有取值方案中,区间最小值的最大值的期望是多少? ...
- SDOI2016 R1做题笔记
SDOI2016 R1做题笔记 经过很久很久的时间,shzr终于做完了SDOI2016一轮的题目. 其实没想到竟然是2016年的题目先做完,因为14年的六个题很早就做了四个了,但是后两个有点开不动.. ...
- SAM 做题笔记(各种技巧,持续更新,SA)
SAM 感性瞎扯. 这里是 SAM 做题笔记. 本来是在一篇随笔里面,然后 Latex 太多加载不过来就分成了两篇. 标 * 的是推荐一做的题目. trick 是我总结的技巧. I. P3804 [模 ...
- C语言程序设计做题笔记之C语言基础知识(下)
C 语言是一种功能强大.简洁的计算机语言,通过它可以编写程序,指挥计算机完成指定的任务.我们可以利用C语言创建程序(即一组指令),并让计算机依指令行 事.并且C是相当灵活的,用于执行计算机程序能完成的 ...
- C语言程序设计做题笔记之C语言基础知识(上)
C语言是一种功能强大.简洁的计算机语言,通过它可以编写程序,指挥计算机完成指定的任务.我们可以利用C语言创建程序(即一组指令),并让计算机依指令行事.并且C是相当灵活的,用于执行计算机程序能完成的几乎 ...
- SDOI2017 R1做题笔记
SDOI2017 R1做题笔记 梦想还是要有的,万一哪天就做完了呢? 也就是说现在还没做完. 哈哈哈我竟然做完了-2019.3.29 20:30
- SDOI2014 R1做题笔记
SDOI2014 R1做题笔记 经过很久很久的时间,shzr又做完了SDOI2014一轮的题目. 但是我不想写做题笔记(
- LCT做题笔记
最近几天打算认真复习LCT,毕竟以前只会板子.正好也可以学点新的用法,这里就用来写做题笔记吧.这个分类比较混乱,主要看感觉,不一定对: 维护森林的LCT 就是最普通,最一般那种的LCT啦.这类题目往往 ...
- java做题笔记
java做题笔记 1. 初始化过程是这样的: 1.首先,初始化父类中的静态成员变量和静态代码块,按照在程序中出现的顺序初始化: 2.然后,初始化子类中的静态成员变量和静态代码块,按照在程序中出现的顺序 ...
随机推荐
- C# WPF:这次把文件拖出去!
首发公众号:Dotnet9 作者:沙漠之尽头的狼 编辑于:成都,2020-12-01 回顾上篇文章:C# WPF:把文件给我拖进来!!! 本文完成对应的下文:<C# WPF:这次把文件拖出去!& ...
- AI伴侣下载
总结 现在网页上很多下载的AI伴侣下载下来都会有些问题或者不能用,如下链接下载的AI伴侣亲测可以使用! (连接后会提示更新,博主没有选择更新,如有需要也可以更新) https://mit-ai2-co ...
- java - 类属性 初始化的三种形式及顺序
package chushihua; public class Hello { public static String name = getValue("属性"); { name ...
- [转帖]TiUP 命令概览
https://docs.pingcap.com/zh/tidb/stable/tiup-reference TiUP 在 TiDB 生态中承担包管理器的功能,管理着 TiDB 生态下众多的组件,如 ...
- [转帖]Kafka主题与分区
https://zhuanlan.zhihu.com/p/428845986#:~:text=%E4%B8%80%E3%80%81kafka-topics.sh%E6%93%8D%E4%BD%9C%2 ...
- [转帖]Linux系统NVME盘分区和挂载
https://www.jianshu.com/p/04327f1b97cb 查看系统里面识别到的硬盘和分区的信息 $ sudo fdisk -l Disk /dev/nvme1n1: 1.8 TiB ...
- [转帖]Windows自带硬盘测试工具使用教程
本教程主要讲解Windows自带的硬盘测试工具的使用,不用再安装第三方软件了.到底准不准就不知道啦,下面我们来看看如何使用吧~ 1. 进入cmd 快速进入cmd 主要如果进入后,使用命令直接闪退,就是 ...
- Linux 下面删除指定日期之前文件的办法
1. Linux 下面最近有一个需求 需要只更新2020年4月10号之后补丁的需求 2. rsync 能够拉取所有的补丁文件 没找到能够按照日期进行拉取的办法. 所以想了一个折中的办法 先拉取 再按 ...
- 麒麟信安V3.4 安装PG15的过程
麒麟信安V3.4 安装PG15的过程 背景 发现基于OpenEuler的几个系统使用CentOS的rpm包 安装PG数据库时有问题. 会提示缺少依赖的so文件. 今天想着解决一下, 就百度了一下并且进 ...
- 【原创】关于xenomai3 RTnet的一点记录
xenomai3协议栈RTnet支持TCP.UDP,但不支持IGMP: 对ARP支持有限制:地址解析的延迟会影响数据包传输延迟,RTnet为实时性考虑,路由表设计静态的,只在设置期间配置,或者接收到其 ...
