【转载】推荐系统 EE 问题与 Bandit 算法

原文地址：

https://toutiao.io/posts/584etm/preview

-------------------------------------------------------------------------

生活中你可能会遇到类似的情况，你在网上购买了手机，淘宝之后会不断给你推送关于手机相关的商品；如果你看了关于NBA詹姆斯的相关新闻，今日头条之后会不断给你推送詹姆斯的新闻。时间长了，你会发现你的世界里只有手机和詹姆斯，天呐，世界越来越小，视野越来越窄怎么办？

别担心，上面的这种情况就属于EE问题的一种，更多的关于什么是推荐系统的EE问题可以参见：推荐系统EE（exploit－explore）问题概述。针对 EE 问题，可以使用 Bandit 算法来解决。这里介绍一些常用的 Bandit 算法。

Naive

Naive 的核心就在于朴素，它的做法就是先进行 N 次尝试，然后统计每个臂的平均收益，接下来一直选择平均收益最大的臂。这个算法是人们在实际中最常采用的。

Epsilon-Greedy（ε-Greedy）

Epsilon-Greedy 通过生成一个 (0,1) 范围内的数字 ε ，用它来表示概率，表示以 ε 的概率去从所有候选臂中随机选择一个，也就是 explore，以 1- ε 的概率去选择平均收益最大的臂，也就是 exploit。

通过 ε 的值可以控制对 explore 和 exploit 的权衡程度， ε 值越小，表明 explore 越保守，会有更好的稳定性。

很明显 ε 数值的确定是一件不容易的事情。

Thompson Sampling（汤普森采样）

介绍汤普森采样之前，可以先来介绍一个分布：beta 分布。beta 分布可以看作一个概率的概率分布，当你不知道一个东西的具体概率是多少时，它可以给出了所有概率出现的可能性大小。

beta 分布有两个控制参数：α 和 β 。先来看下几个 beta 分布的概率密度函数的图形：

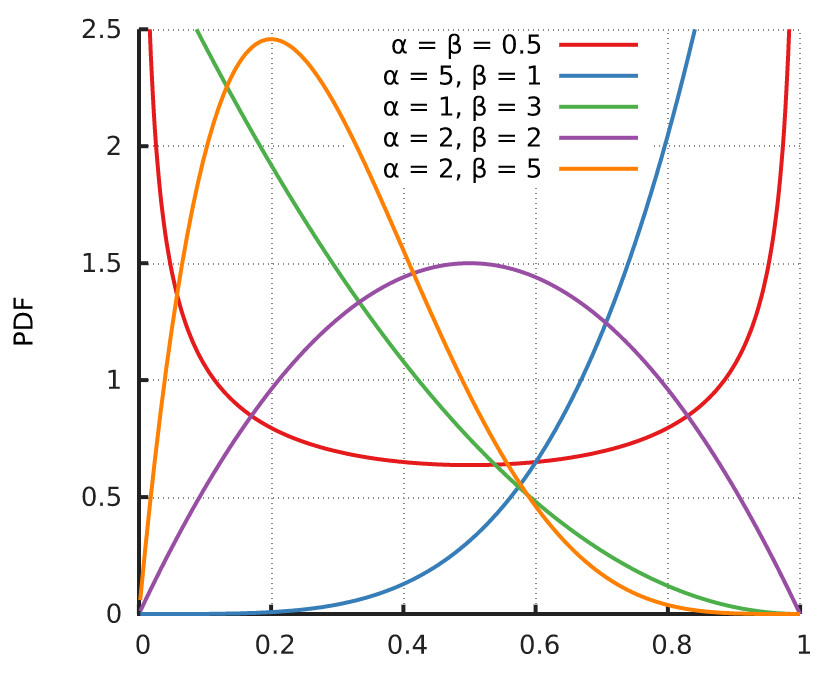
beta 分布图形中的 x 轴取值范围是 (0,1)，可以看成是概率值，参数 α 和 β 可以控制图形的形状和位置：

α + β 的值越大，分布曲线越窄，也就是越集中。
α/(α + β) 的值是 beta 分布的均值（期望值），它的值越大， beta 分布的中心越靠近 1，否则越靠近 0 。

注意：当参数 α 和 β 确定后，使用 beta 分布生成的随机数有可能不一样，所以汤普森采样法是不确定算法。

beta 分布和 Bandit 算法有什么关联呢？实际上，每个臂是否产生收益的概率 p 的背后都对应一个 beta 分布。我们将 beta 分布的 α 参数看成是推荐后用户的点击次数， β 参数看成是推荐后用户未点击的次数。

来看下使用汤普森算法的流程：

每个臂都维护一个 beta 分布的参数，获取每个臂对应的参数 α 和 β，然后使用 beta 分布生成随机数。
选取生成随机数最大的那个臂作为本次结果
观察用户反馈，如果用户点击则将对应臂的 α 加 1，否则 β 加 1

在实际的推荐系统中，需要为每个用户保存一套参数，假设有 m 个用户， n 个臂（选项，可以是物品，可以是策略），每个臂包含 α 和 β 两个参数，所以最后保存的参数的总个数是 2 m n。

可以直观的理解下为什么汤普森采样算法有效：

当尝试的次数较多时，即每个臂的 α + β 的值都很大，这时候每个臂对应的 beta 分布都会很窄，也就是说，生成的随机数都非常接近中心位置，每个臂的收益基本确定了。
当尝试的次数较少时，即每个臂的 α + β 的值都很小，这时候每个臂对应的 beta 分布都会很宽，生成的随机数有可能会比较大，增加被选中的机会。
当一个臂的 α + β 的值很大，并且 α/(α + β) 的值也很大，那么这个臂对应的 beta 分布会很窄，并且中心位置接近 1 ，那么这个臂每次选择时都很占优势。

使用 python 来实现汤普森采样：

import  numpy as np

import  pymc

# wins 和 trials 都是一个 N 维向量，N 是臂的个数

# wins 表示所有臂的 α 参数，loses 表示所有臂的 β 参数

choice = np.argmax(pymc.rbeta(1 + wins, 1 + loses, len(wins)))

# wins[choice] += 1

# loses[choice] += 1

UCB（Upper Confidence Bound）

UCB 算法全称是 Upper Confidence Bound，即置信区间上界。它是计算每个臂的平均收益与该收益的不确定性来作为最终得分。公式如下：

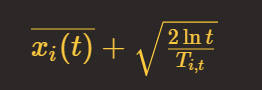
i 表示当前的臂，t 表示目前的尝试次数，Ti,t 表示臂 i 被选中的次数。公式加号左边表示臂 i 当前的平均收益，右边表示该收益的 Bonus ，本质上是均值的标准差，反应了候选臂效果的不确定性，就是置信区间的上边界。

使用 UCB 算法的流程如下：

对所有臂先尝试一次
按照公式计算每个臂的最终得分
选择得分最高的臂作为本次结果

直观理解下 UCB 算法为什么有效？

当一个臂的平均收益较大时，也就是公式左边较大，在每次选择时占有优势
当一个臂被选中的次数较少时，即 Tit 较小，那么它的 Bonus 较大，在每次选择时占有优势

所以 UCB 算法倾向选择被选中次数较少以及平均收益较大的臂。

UCB 算法需要对所有的臂进行一次尝试，当臂比较多时，可能会比较耗时，如果 UCB 算法的参数是确定的，那么输出结果就是确定的，也就是说它本质上仍然是一个“确定性”的算法，这会导致它的 explore 能力受限。

总结

为解决推荐系统 EE 问题，可以使用 Bandit 算法，这里介绍了常用的 Bandit 算法，如：Naive、Epsilon-Greedy（ε-Greedy）、UCB（Upper Confidence Bound）等，但是这些算法都没有考虑上下文信息，也就是环境，之后会介绍结合上下文信息的 LinUCB 算法。