tensorflow语法【tf.concat()详解】

相关文章：

【一】tensorflow安装、常用python镜像源、tensorflow 深度学习强化学习教学

【二】tensorflow调试报错、tensorflow 深度学习强化学习教学

【三】tensorboard安装、使用教学以及遇到的问题

【四】超级快速pytorch安装

---

trick1---实现tensorflow和pytorch迁移环境教

---

tf.concat()是相对比较好理解的函数，它和python里的numpy.concatenate()函数作用是一样的。都是把多个array沿着某一个维度接在一起。只不过numpy.concatenate()用来处理numpy array，tf.concat()用于处理tensor。他们俩有个共同点，就是得到的结果tensor或者numpy array的维度的数量一定是一样的。

例子：

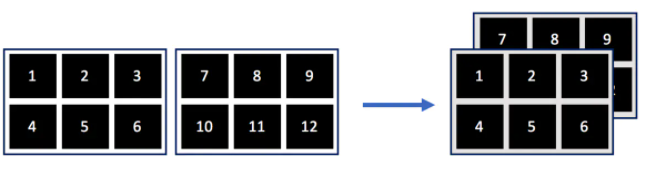
t1 = [[1, 2, 3], [4, 5, 6]]
t2 = [[7, 8, 9], [10, 11, 12]]
tf.concat([t1, t2], 0)  

输出结果：

[[1, 2, 3], [4, 5, 6], [7, 8, 9], [10, 11, 12]]
shape=[4, 3]

先来分解一下t1和t2。首先t1 = [[1, 2, 3], [4, 5, 6]]可以看成：

t1 = [A, B]
A = [1,2,3]
B = [4,5,6]

t1的shape是[2,3]，意思是有2个元素[A, B], 他们每个里面有3个元素，t2同理。

t2 = [C, D]
C = [7,8,9]
D = [10,11,12]

这里[2,3]的维度数量是2，也就是2维的。如果是3维的可能是[2,3,什么]。知道tf.concat()不会改变维度数量非常重要。因为tf.concat()只是对对应维度元素数量的叠加。比如tf.concat([t1, t2], 0)意思是对t1和t2在第一维度对接。因为他俩的shape都是[2,3]，输出tensor的shape一定是[4,3]，因为他俩的第一维度都是2，2+2=4。再比如如果是tf.concat([t1, t2], 1)，那么输出shape一定是[2,6]，以此类推。

维度是从0开始算的，也就是沿着第一个维度接起来。(以此类推，axis=1就是第二个维度)，从shape可以看出t1和t2都是只有两个维度。既然是沿着第一个维度对接，那根本就不用看第二个维度。

那么什么是第一个维度呢？就可以理解成第一层中括号。t1的第一层中括号是t1 = [A, B]， t2 = [C, D]（展开A,B,C,D是第二个维度）
那对接是什么意思呢？就是把对应的中括号打开，把对应的里面一层的元素放在一起，再用中括号全扩起来。

tf.concat([t1, t2], 0)  #后面的0的意思是 axis=0

按步骤是：

1. 打开中括号：[A,B],[C,D] -> A,B,C,D
2. 放在一起再扩起来: A,B,C,D -> [A,B,C,D]

这里已经知道了输出的shape是[4,3]。其中的4代表第一维度有4个元素，就是A,B,C,D。t1 = [A, B]， t2 = [C, D]各只有一个中括号，所以不用考虑对应，直接放一起就行了。如果t1和t2比如各有2个中括号的话，括回去之后也应该有2个中括号，下面例2有讲到

A,B,C,D都是什么来着？

A = [1,2,3]
B = [4,5,6]
C = [7,8,9]
D = [10,11,12]

每个里面有3个元素，这就是[4,3]的3的含义。
所以输出结果是:

[[1, 2, 3], [4, 5, 6], [7, 8, 9], [10, 11, 12]], shape = [4,3]

注意t1和t2是有顺序的。如果这行命令是：

tf.concat([t2, t1], 0)

那么结果应该是[[7, 8, 9], [10, 11, 12], [1, 2, 3], [4, 5, 6]]

tf.concat([t1, t2], 1)  #1是 axis=1，第二维度的意思

还是按照上面的方法，我们知道了输出结果的shape一定是[2,6]。既然沿着第二维度对接，那么不用看第一维度。
第一维度是：t1 = [A, B]， t2 = [C, D]（不用动,也就是这一维度的输出结果一定是[x1, x2]）
第二维度是：A = [1,2,3] B = [4,5,6] C = [7,8,9] D = [10,11,12]
这里A,B属于t1，C,D属于t2，各有2个中括号。那么按顺序，A对应C，B对应D。

1. 打开中括号：[1,2,3],[4,5,6],[7,8,9],[10,11,12] -> 1,2,3, 4,5,6, 7,8,9, 10,11,12
2. 对应的A,C放一起：1,2,3,7,8,9 -> [1,2,3,7,8,9]
3. 对应的B,D放一起: 4,5,6,10,11,12 -> [4,5,6,10,11,12]

最后在第一维度括起来，结果是：

[[1, 2, 3, 7, 8, 9], [4, 5, 6, 10, 11, 12]], shape = [2,6]

直观方法：

t1 = [[1, 2, 3], [4, 5, 6]]
t2 = [[7, 8, 9], [10, 11, 12]]
tf.concat([t1, t2], 0)  

其实t1是个2维数组，也就是一个面。形象一点就是：

t1:
-------
|1|2|3|
|-|-|-|
|4|5|6|
-------
t2:
----------
| 7| 8| 9|
|--|--|--|
|10|11|12|
----------

都是2行3列。
我会把第一维度看成行，第二维度看成列。
如果沿着行对接，也就是把行数增加为4行，列数还是3列。那么结果就是：

----------
| 1| 2| 3|
|--|--|--|
| 4| 5| 6|
----------
| 7| 8| 9|
|--|--|--|
|10|11|12|
----------

这个矩阵就是：

[[1, 2, 3],
[4, 5, 6],
[7, 8, 9],
[10, 11, 12]]

demo2：

t1 = [[1, 2, 3], [4, 5, 6]]
t2 = [[7, 8, 9], [10, 11, 12]]
tf.concat([t1, t2], 1)  

这就是沿着列对接，也就是变成6列。行还是3行。也就变成了：

-------------------
| 1| 2| 3| 7| 8| 9|
|--|--|--|--|--|--|
| 4| 5| 6|10|11|12|
-------------------

输出就是

[[1, 2, 3, 7, 8, 9],
[4, 5, 6, 10, 11, 12]]

如果两个tensor都有第三维的话，比如：

t1 = [[[1], [2], [3]], [[4], [5], [6]]]
t2 = [[[7], [8], [9]], [[10], [11], [12]]]
tf.concat([t1, t2], 2)  

t1和t2的shape都是[2,3,1]，沿着第三维对接。结果shape一定是[2,3,2]。
那么用这个直观的方法就是非常好理解，
就可以理解成把t1的2d矩阵放在t2的2d矩阵的前面，形成一个3d矩阵，像这样：

3d数组这样理解：2行，3列，2层
2行：[A, B]
3列：A = [a,b,c], B = [d, e, f]
2层：a = [1,7], b = [2,8], c = [3, 9], d = [4, 10], e = [5, 11], f = [6, 12]
所以结果是：

[[[1,7], [2,8], [3, 9]], [[4, 10], [5, 11], [6, 12]]], shape = [2,3,2]

这种方法的弊端就是大于3维的数组就不好想了，毕竟我们生活的是3维世界。

链接：https://www.jianshu.com/p/c465e7fab882