KMP算法的来龙去脉
1. 引言
字符串匹配是极为常见的一种模式匹配。简单地说,就是判断主串TT中是否出现该模式串PP,即PP为TT的子串。特别地,定义主串为T[0…n−1]T[0…n−1],模式串为P[0…p−1]P[0…p−1],则主串与模式串的长度各为nn与pp。
暴力匹配
暴力匹配方法的思想非常朴素:
- 依次从主串的首字符开始,与模式串逐一进行匹配;
- 遇到失配时,则移到主串的第二个字符,将其与模式串首字符比较,逐一进行匹配;
- 重复上述步骤,直至能匹配上,或剩下主串的长度不足以进行匹配。
下图给出了暴力匹配的例子,主串T="ababcabcacbab",模式串P="abcac",第一次匹配:
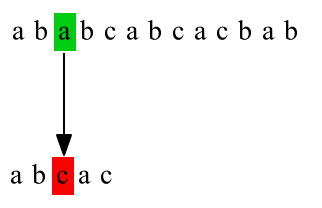
第二次匹配:
第三次匹配: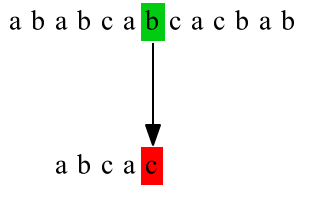
C代码实现:
int brute_force_match(char *t, char *p) {
int i, j, tem;
int tlen = strlen(t), plen = strlen(p);
for(i = 0, j = 0; i <= tlen - plen; i++, j = 0) {
tem = i;
while(t[tem] == p[j] & j < plen) {
tem++;
j++;
}
// matched
if(j == plen) {
return i;
}
}
// [p] is not a substring of [t]
return -1;
}时间复杂度:i在主串移动次数(外层的for循环)有n−pn−p次,在失配时j移动次数最多有p−1p−1次(最坏情况下);因此,复杂度为O(n∗p)O(n∗p)。
我们仔细观察暴力匹配方法,发现:失配后下一次匹配,
- 主串的起始位置 = 上一轮匹配的起始位置 + 1;
- 模式串的起始位置 = 首字符
P[0]。
如此未能利用已经匹配上的字符的信息,造成了重复匹配。举个例子,比如:第一次匹配失败时,主串、模式串失配位置的字符分别为 a 与 c,下一次匹配时主串、模式串的起始位置分别为T[1]与P[0];而在模式串中c之前是ab,未有重复字符结构,因此T[1]与P[0]肯定不能匹配上,这样造成了重复匹配。直观上,下一次的匹配应从T[2]与P[0]开始。
2. KMP算法
KMP思想
根据暴力方法的缺点,而引出KMP算法的思想。首先,一般化匹配失败,如下图所示:
在暴力匹配方法中,下一次匹配开始时,主串指针会回溯到i+1,模式串指针会回退到0。那么,如果不让主串指针发生回溯,模式串的指针应回退到哪个位置才能保证正确匹配呢?首先,我们从上图中可以得到已匹配上的字符:
KMP算法思想便是利用已经匹配上的字符信息,使得模式串的指针回退的字符位置能将主串与模式串已经匹配上的字符结构重新对齐。当有重复字符结构时,下一次匹配如下图所示:

从图中可以看出,下一次匹配开始时,主串指针在失配位置i+j,模式串指针回退到m+1;模式串的重复字符结构:
且有
那么应如何选取mm值呢?假定有满足式子(1)(1)的两个值m1>m2m1>m2,如下图所示: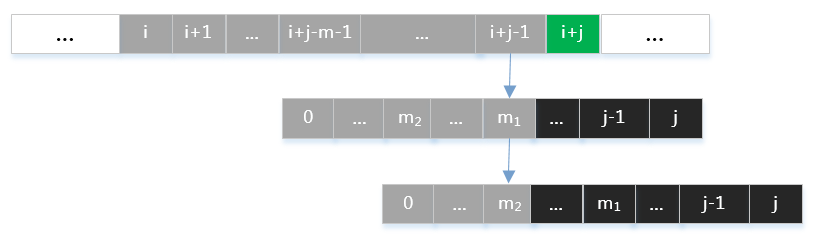
如果选取m=m2m=m2,则会丢失m=m1m=m1的这一种字符匹配情况。由数学归纳法容易知道,应取所有满足式子(1)(1)中最大的mm值。
KMP算法中每一次的匹配,
- 主串的起始位置 = 上一轮匹配的失配位置;
- 模式串的起始位置 = 重复字符结构的下一位字符(无重复字符结构,则模式串的首字符)
模式串P="abcac"匹配主串T="ababcabcacbab"的KMP过程如下图: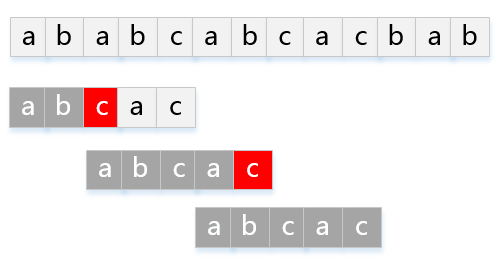
部分匹配函数
根据上面的讨论,我们定义部分匹配函数(Partial Match,在数据结构书[2]称之为失配函数):
其表示字符串P[0…j]P[0…j]的前缀与后缀完全匹配的最大长度,也表示了模式串中重复字符结构信息。KMP中大名鼎鼎的next[j]函数表示对于模式串失配位置j+1,下一轮匹配时模式串的起始位置(即对齐于主串的失配位置);则
如何计算部分匹配函数呢?首先来看一个例子,模式串P="ababababca"的部分匹配函数与next函数如下:
| j | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| P[j] | a | b | a | b | a | b | a | b | c | a | |
| f(j) | -1 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | -1 | 0 | |
| next[j] | 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 0 | 1 |
模式串的f(j)满足P[0…f(j)]=P[j−f(j)…j]P[0…f(j)]=P[j−f(j)…j],在计算f(j+1)分为两类情况:
- 若P[j+1]=P[f(j)+1]P[j+1]=P[f(j)+1],则有P[0…f(j)+1]=P[j−f(j)…j+1]P[0…f(j)+1]=P[j−f(j)…j+1],因此
f(j+1)=f(j)+1。 - 若P[j+1]≠P[f(j)+1]P[j+1]≠P[f(j)+1],则要从P[0…f(j)]P[0…f(j)]中找出满足
P[f(j+1)]=P[j+1]的f(j+1),从而得到P[0…f(j+1)]=P[j+1−f(j+1)…j+1]P[0…f(j+1)]=P[j+1−f(j+1)…j+1]
其中,根据f(j)的定义有:
其中,fk(j)=f(fk−1(j))fk(j)=f(fk−1(j))。通过上面的例子可知,函数fk(j)fk(j)是随着kk递减的,并最后收敛于-1。此外,P[j]与p[j+1]相邻;因此若存在P[f(j+1)]=P[j+1],则必有
为了求满足条件的最大的f(j+1),因fk(j)fk(j)是随着kk递减的,故应为满足上式的最小kk值。
综上,部分匹配函数的计算公式如下:
代码实现
部分匹配函数(失配函数)的C实现代码:
int *fail(char *p) {
int len = strlen(p);
int *f = (int *) malloc(len * sizeof(int));
f[0] = -1;
int i, j;
for(j = 1; j < len; j++) {
for(i = f[j-1]; ; i = f[i]) {
if(p[j] == p[i+1]) {
f[j] = i + 1;
break;
}
else if(i == -1) {
f[j] = -1;
break;
}
}
}
return f;
}KMP的C实现代码:
int kmp(char *t, char *p) {
int *f = fail(p);
int i, j;
for(i = 0, j = 0; i < strlen(t) && j < strlen(p); ) {
if(t[i] == p[j]) {
i++;
j++;
}
else if(j == 0)
i++;
else
j = f[j-1] + 1;
}
return j == strlen(p) ? i - strlen(p) : -1;
}时间复杂度:fail函数的复杂度为O(p)O(p),kmp函数的复杂度为O(n)O(n),所以整个KMP算法的复杂度为O(n+p)O(n+p)。
KMP算法的来龙去脉的更多相关文章
- 【模式匹配】KMP算法的来龙去脉
1. 引言 字符串匹配是极为常见的一种模式匹配.简单地说,就是判断主串\(T\)中是否出现该模式串\(P\),即\(P\)为\(T\)的子串.特别地,定义主串为\(T[0 \dots n-1]\),模 ...
- 深入理解KMP算法之续篇
前言: 纠结于KMP已经两天了,相较于本人之前博客中提到的几篇博文,本人感觉这篇文章更清楚地说明了KMP算法的来龙去脉. http://www.cnblogs.com/goagent/archive/ ...
- KMP算法具体解释(转)
作者:July. 出处:http://blog.csdn.net/v_JULY_v/. 引记 此前一天,一位MS的朋友邀我一起去与他讨论高速排序,红黑树,字典树,B树.后缀树,包含KMP算法,只有在解 ...
- 简单有效的kmp算法
以前看过kmp算法,当时接触后总感觉好深奥啊,抱着数据结构的数啃了一中午,最终才大致看懂,后来提起kmp也只剩下“奥,它是做模式匹配的”这点干货.最近有空,翻出来算法导论看看,原来就是这么简单(先不说 ...
- KMP算法
KMP算法是字符串模式匹配当中最经典的算法,原来大二学数据结构的有讲,但是当时只是记住了原理,但不知道代码实现,今天终于是完成了KMP的代码实现.原理KMP的原理其实很简单,给定一个字符串和一个模式串 ...
- 萌新笔记——用KMP算法与Trie字典树实现屏蔽敏感词(UTF-8编码)
前几天写好了字典,又刚好重温了KMP算法,恰逢遇到朋友吐槽最近被和谐的词越来越多了,于是突发奇想,想要自己实现一下敏感词屏蔽. 基本敏感词的屏蔽说起来很简单,只要把字符串中的敏感词替换成"* ...
- KMP算法实现
链接:http://blog.csdn.net/joylnwang/article/details/6778316 KMP算法是一种很经典的字符串匹配算法,链接中的讲解已经是很明确得了,自己按照其讲解 ...
- 数据结构与算法JavaScript (五) 串(经典KMP算法)
KMP算法和BM算法 KMP是前缀匹配和BM后缀匹配的经典算法,看得出来前缀匹配和后缀匹配的区别就仅仅在于比较的顺序不同 前缀匹配是指:模式串和母串的比较从左到右,模式串的移动也是从 左到右 后缀匹配 ...
- 扩展KMP算法
一 问题定义 给定母串S和子串T,定义n为母串S的长度,m为子串T的长度,suffix[i]为第i个字符开始的母串S的后缀子串,extend[i]为suffix[i]与字串T的最长公共前缀长度.求出所 ...
随机推荐
- VMware Workstation 12 Pro 之安装林耐斯优麒麟 X64-UI系统
VMware Workstation 12 Pro 之安装林耐斯优麒麟 X64-UI系统... ------------------------------- -------------------- ...
- jQuery ajax error函数(交互错误信息的获取)
一般error函数返回的参数有三个: function(jqXHR jqXHR, String textStatus, String errorThrown).常见调用代码如下: $.ajax({ u ...
- Microsoft Azure Storage Exployer使用指南
概述 Microsoft Azure Storage Exployer 是微软官方推荐的一款管理Azure Storage 客户端工具,客户使用完全免费.支持Windows.Mac和Linux.用户使 ...
- MyBatis记录
记录一下MyBatis的几个模块大纲,除去缓存以及集合映射两个部分 Mybatis架构 1. mybatis配置 SqlMapConfig.xml,此文件作为mybatis的全局配置文件,配置了myb ...
- GoogleNet:inceptionV3论文学习
Rethinking the Inception Architecture for Computer Vision 论文地址:https://arxiv.org/abs/1512.00567 Abst ...
- 启动tomcat错误:Address already in use: JVM_Bind:8081
解决方法: 1.打开任务管理器,关闭掉javaw进程. 2.修改tomcat端口:tomcat/conf/server.xml
- 在JS事件封装时,addEventListener()方法的this问题
最近在写js的类库,模仿的是jquery的编程风格,当封装到事件监听的时候发现遇到了一个问题,代码是这样的: 上面是封装的一个事件委托的代码,我以为上面的封装跟普通的事件监听一样简单,结果我在调用时发 ...
- json对象和json字符串之间的转化
json对象和json字符串之间的转化 json字符串----->json对象 使用JSON.parse()函数 var jsonStr = '{"name":"z ...
- 关于本地代码挂载到vm虚拟环境下运行
第一步: 首先你得装个 VM 虚拟机 然后新建一个Linux虚拟环境(建议CentOS镜像)(PS:至于安装此处就省略.....) 第二步:启动虚拟机配置 lnmp (这里我们可以使用 lnmp的 ...
- 大道至简第一章观后感——java伪代码
一节: public class Yugongyishan_ { //定义一个名为Yugongyishan_的类 Public static void main(string args[]) // ...
