凸包GiftWrapping GrahamScan 算法实现

开始

游戏内有需求做多边形碰撞功能，但是接入box2d相对游戏的需求来说太重度了。所以准备自己实现碰撞。

确定多边形，必然要用到凸包的算法。在github上也找到了一些lua实现,但是这里的算法没有考虑多点共线的问题。所以准备自己实现

准备

这里提到的所有凸包，都指的平面上的。

• 思路

凸包的具体定义，这里不赘述。一种通俗的说法，在木板上钉钉子，我们用一根麻绳绑住一个外面的钉子然后拉着麻绳绕所有钉子一圈这个麻绳围成的圈最后也构成了钉子组成的点集的凸包。

其实这种说法，和GiftWrapping算法的实现也有点异曲同工的感觉。 也就是先确定一个最边缘的点A，然后逆时针顺序寻找下一个与A构成的向量在逆时针方向上旋转角度最小的点。如果寻找到下一个点B，则继续用B点做基础点，寻找下一个点。直到寻找到的点为A，才会完成。

这里借用一下booble的图，画图好麻烦

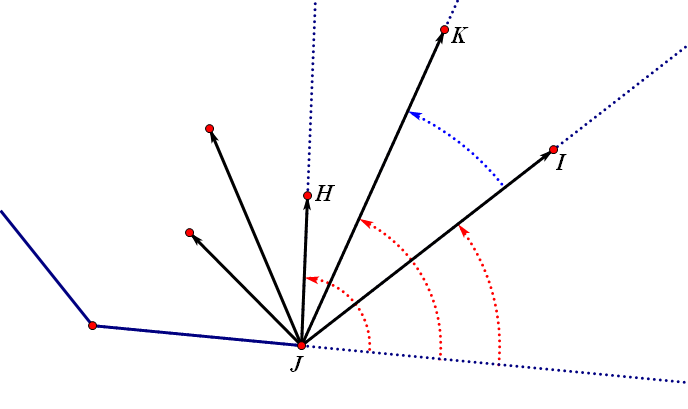
了解更多GiftWrapping点这里，只不过这里的图示显示的是顺时针确定点的

• 寻找下一个逆时针方向旋转角度最小的点

虽然可以直接通过两点计算出构成的向量的角度，然后进行排序比较，但是性能太差了。这里主要是用到向量叉积,因为不需要知道确定的旋转角度，只要能比较大小就可以了

向量叉积的特性：向量A乘以向量B，如果结果为正，则A逆时针旋转向B，则A向量相对于B逆时针方向旋转角度更小；否则为B更小； 如果为0，则共线。这里必须保证的是A旋转到B的角度必须小于180，否则会出错。这也就是为什么一开始要选一个最边缘的点做基础点的原因。

• 共线的问题

如果两个向量叉积的结果为0，则两个向量共线了。因为这里只是确定凸多边形，而距离近的点必然是在基础点与较远点组成的边上，所以舍弃近距离点

实现

• 获取第一个基础点

这里获取最左点，即X最小的点。如果又多个，取这些点中，y最小的点

local function getLeftIndex(points)
	local size = #points
	local leftIndex = 1
	for i=2,size do
		if points[i].x < points[leftIndex].x
		then
			leftIndex = i
		end

		if 	points[i].x == points[leftIndex].x
		and points[i].y < points[leftIndex].y
		then
			leftIndex = i
		end
	end
	return leftIndex
end

• 比较一个哪个点与基础点形成的向量逆时针旋转更小

这里不多说，注释写的很明确了

--叉积
local function cross(p1,p2,p3)
 	return 	(p2.x - p1.x)*(p3.y - p1.y)
   	      - (p2.y - p1.y)*(p3.x - p1.x)
end 

--距离
local function longer(startP,endP1,endP2)
 	return ((endP2.x - startP.x)^2 + (endP2.y - startP.y)^2)
  		-  ((endP1.x - startP.x)^2 + (endP1.y - startP.y)^2)
  		>  Deviation
end

--判断(startP,midP)组成向量 a 是否顺时针旋转一个在 [0,180)区间的角度 β 后能与(startP,checkP)组成的向量 b 共线
--如果β 在(0,180)范围，则返回true
--如果β == 0 若，|b| > |a| 则，返回true 注意：如果midp 和 checkP是在误差范围内的相同点，返回的是false
local function isBetterVertice(startP,midP,checkP)
	local crossResult = cross(startP,midP,checkP)
	--crossResult0 则，逆时针
	-- =0 则，共线
	if  crossResult < 0 then
	 return true
	end

	if crossResult < Deviation
	and longer(startP,midP,checkP)
	then
		return true
	end

	return false
end

• 完成GiftWrapping算法

local function giftWrapping(points)
	local  pointCount = #points
	if pointCount < 3 then return nil end

	local leftIndex = getLeftIndex(points)
	local preIndex = leftIndex
	local hull = {}
	repeat
		table.insert(hull,#hull+1,points[preIndex])
		local bestIndex = 1

		for i=2,pointCount do
			if  bestIndex == preIndex
			or  isBetterVertice(points[preIndex],points[bestIndex],points[i])
			then
				bestIndex = i
			end
		end

		preIndex = bestIndex
	until (preIndex == leftIndex)

	return hull
end

• 完整代码在这里

这个代码里顺带实现了GrahamScan，因为这个算法最麻烦的是确定一最左基础点后的剩余点按逆时针角度排序。但是排序要用的compare 方法，之前用到的isBetterVertice 完全可以胜任这个功能，就顺手写出来了。 GrahamScan相关

• 其他

如有错误多包涵，轻喷

之后开始记录一下碰撞的东西，主要是多边形碰撞以及圆与多边形碰撞

转载请注明出处

http://www.cnblogs.com/boliu/p/4109120.html