MCMC(二)马尔科夫链

　　　　MCMC(一)蒙特卡罗方法

　　　　MCMC(二)马尔科夫链

　　　　MCMC(三)MCMC采样和M-H采样

　　　　MCMC(四)Gibbs采样

　　　　在MCMC(一)蒙特卡罗方法中，我们讲到了如何用蒙特卡罗方法来随机模拟求解一些复杂的连续积分或者离散求和的方法，但是这个方法需要得到对应的概率分布的样本集，而想得到这样的样本集很困难。因此我们需要本篇讲到的马尔科夫链来帮忙。

1. 马尔科夫链概述

　　　　马尔科夫链定义本身比较简单，它假设某一时刻状态转移的概率只依赖于它的前一个状态。举个形象的比喻，假如每天的天气是一个状态的话，那个今天是不是晴天只依赖于昨天的天气，而和前天的天气没有任何关系。当然这么说可能有些武断，但是这样做可以大大简化模型的复杂度，因此马尔科夫链在很多时间序列模型中得到广泛的应用，比如循环神经网络RNN，隐式马尔科夫模型HMM等，当然MCMC也需要它。

　　　　如果用精确的数学定义来描述，则假设我们的序列状态是$...X_{t-2}, X_{t-1}, X_{t},  X_{t+1},...$，那么我们的在时刻$X_{t+1}$的状态的条件概率仅仅依赖于时刻$X_{t}$，即：$$P(X_{t+1} |...X_{t-2}, X_{t-1}, X_{t} ) = P(X_{t+1} | X_{t})$$

　　　　既然某一时刻状态转移的概率只依赖于它的前一个状态，那么我们只要能求出系统中任意两个状态之间的转换概率，这个马尔科夫链的模型就定了。我们来看看下图这个马尔科夫链模型的具体的例子(来源于维基百科)。

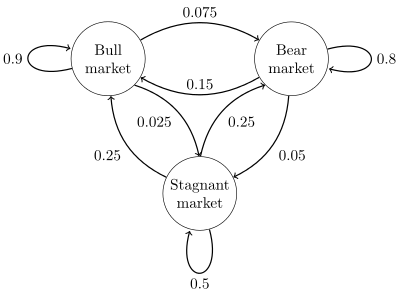　　　　这个马尔科夫链是表示股市模型的，共有三种状态：牛市（Bull market）, 熊市（Bear market）和横盘（Stagnant market）。每一个状态都以一定的概率转化到下一个状态。比如，牛市以0.025的概率转化到横盘的状态。这个状态概率转化图可以以矩阵的形式表示。如果我们定义矩阵阵$P$某一位置$P(i,j)$的值为$P(j|i)$,即从状态i转化到状态j的概率，并定义牛市为状态0， 熊市为状态1, 横盘为状态2. 这样我们得到了马尔科夫链模型的状态转移矩阵为：$$P=\left( \begin{array}{ccc}
0.9&0.075&0.025 \\ 0.15&0.8& 0.05 \\
0.25&0.25&0.5 \end{array} \right)$$

　　　　讲了这么多，那么马尔科夫链模型的状态转移矩阵和我们蒙特卡罗方法需要的概率分布样本集有什么关系呢？这需要从马尔科夫链模型的状态转移矩阵的性质讲起。

2. 马尔科夫链模型状态转移矩阵的性质

　　　　得到了马尔科夫链模型的状态转移矩阵，我们来看看马尔科夫链模型的状态转移矩阵的性质。

　　　　完整代码参见我的github:https://github.com/ljpzzz/machinelearning/blob/master/mathematics/mcmc_2.ipynb

　　　　仍然以上面的这个状态转移矩阵为例。假设我们当前股市的概率分布为：[0.3,0.4,0.3],即30%概率的牛市，40%概率的熊盘与30%的横盘。然后这个状态作为序列概率分布的初始状态$t_0$，将其带入这个状态转移矩阵计算$t_1, t_2,t_3...$的状态。代码如下：

import numpy as np
matrix = np.matrix([[0.9,0.075,0.025],[0.15,0.8,0.05],[0.25,0.25,0.5]], dtype=float)
vector1 = np.matrix([[0.3,0.4,0.3]], dtype=float)
for i in range(100):
    vector1 = vector1*matrix
    print "Current round:" , i+1
    print vector1

　　　　部分输出结果如下：

Current round: 1
[[ 0.405   0.4175  0.1775]]
Current round: 2
[[ 0.4715   0.40875  0.11975]]
Current round: 3
[[ 0.5156  0.3923  0.0921]]
Current round: 4
[[ 0.54591   0.375535  0.078555]]
。。。。。。
Current round: 58
[[ 0.62499999  0.31250001  0.0625    ]]
Current round: 59
[[ 0.62499999  0.3125      0.0625    ]]
Current round: 60
[[ 0.625   0.3125  0.0625]]
。。。。。。
Current round: 99
[[ 0.625   0.3125  0.0625]]
Current round: 100
[[ 0.625   0.3125  0.0625]]

　　　　可以发现，从第60轮开始，我们的状态概率分布就不变了，一直保持在[0.625   0.3125  0.0625]，即62.5%的牛市，31.25%的熊市与6.25%的横盘。那么这个是巧合吗？

　　　　我们现在换一个初始概率分布试一试，现在我们用[0.7,0.1,0.2]作为初始概率分布，然后这个状态作为序列概率分布的初始状态$t_0$，将其带入这个状态转移矩阵计算$t_1, t_2,t_3...$的状态。代码如下：

matrix = np.matrix([[0.9,0.075,0.025],[0.15,0.8,0.05],[0.25,0.25,0.5]], dtype=float)
vector1 = np.matrix([[0.7,0.1,0.2]], dtype=float)
for i in range(100):
    vector1 = vector1*matrix
    print "Current round:" , i+1
    print vector1

　　　　部分输出结果如下：

Current round: 1
[[ 0.695   0.1825  0.1225]]
Current round: 2
[[ 0.6835   0.22875  0.08775]]
Current round: 3
[[ 0.6714  0.2562  0.0724]]
Current round: 4
[[ 0.66079   0.273415  0.065795]]
。。。。。。。
Current round: 55
[[ 0.62500001  0.31249999  0.0625    ]]
Current round: 56
[[ 0.62500001  0.31249999  0.0625    ]]
Current round: 57
[[ 0.625   0.3125  0.0625]]
。。。。。。。
Current round: 99
[[ 0.625   0.3125  0.0625]]
Current round: 100
[[ 0.625   0.3125  0.0625]]

　　　　可以看出，尽管这次我们采用了不同初始概率分布，最终状态的概率分布趋于同一个稳定的概率分布[0.625   0.3125  0.0625]， 也就是说我们的马尔科夫链模型的状态转移矩阵收敛到的稳定概率分布与我们的初始状态概率分布无关。这是一个非常好的性质，也就是说，如果我们得到了这个稳定概率分布对应的马尔科夫链模型的状态转移矩阵，则我们可以用任意的概率分布样本开始，带入马尔科夫链模型的状态转移矩阵，这样经过一些序列的转换，最终就可以得到符合对应稳定概率分布的样本。

　　　　这个性质不光对我们上面的状态转移矩阵有效，对于绝大多数的其他的马尔科夫链模型的状态转移矩阵也有效。同时不光是离散状态，连续状态时也成立。

　　　　同时，对于一个确定的状态转移矩阵$P$，它的n次幂$P^n$在当n大于一定的值的时候也可以发现是确定的，我们还是以上面的例子为例，计算代码如下：

matrix = np.matrix([[0.9,0.075,0.025],[0.15,0.8,0.05],[0.25,0.25,0.5]], dtype=float)
for i in range(10):
    matrix = matrix*matrix
    print "Current round:" , i+1
    print matrix

　　　　输出结果如下：

Current round: 1
[[ 0.8275   0.13375  0.03875]
 [ 0.2675   0.66375  0.06875]
 [ 0.3875   0.34375  0.26875]]
Current round: 2
[[ 0.73555   0.212775  0.051675]
 [ 0.42555   0.499975  0.074475]
 [ 0.51675   0.372375  0.110875]]
。。。。。。
Current round: 5
[[ 0.62502532  0.31247685  0.06249783]
 [ 0.6249537   0.31254233  0.06250397]
 [ 0.62497828  0.31251986  0.06250186]]
Current round: 6
[[ 0.625   0.3125  0.0625]
 [ 0.625   0.3125  0.0625]
 [ 0.625   0.3125  0.0625]]
Current round: 7
[[ 0.625   0.3125  0.0625]
 [ 0.625   0.3125  0.0625]
 [ 0.625   0.3125  0.0625]]
。。。。。。
Current round: 9
[[ 0.625   0.3125  0.0625]
 [ 0.625   0.3125  0.0625]
 [ 0.625   0.3125  0.0625]]
Current round: 10
[[ 0.625   0.3125  0.0625]
 [ 0.625   0.3125  0.0625]
 [ 0.625   0.3125  0.0625]]　　

　　　　我们可以发现，在$n \geq 6$以后，$P^n$的值稳定不再变化，而且每一行都为[0.625   0.3125  0.0625]，这和我们前面的稳定分布是一致的。这个性质同样不光是离散状态，连续状态时也成立。

　　　　好了，现在我们可以用数学语言总结下马尔科夫链的收敛性质了：

　　　　如果一个非周期的马尔科夫链有状态转移矩阵$P$, 并且它的任何两个状态是连通的，那么$\lim_{n \to \infty}P_{ij}^n$与i无关，我们有：

　　　　1）$$\lim_{n \to \infty}P_{ij}^n = \pi(j)$$

　　　　2) $$\lim_{n \to \infty}P^n = \left( \begin{array}{ccc}
\pi(1)&\pi(2)&\ldots&\pi(j)&\ldots \\ \pi(1)&\pi(2)&\ldots&\pi(j)&\ldots \\ \ldots&\ldots&\ldots&\ldots&\ldots \\ \pi(1)&\pi(2)&\ldots&\pi(j)&\ldots \\
\ldots&\ldots&\ldots&\ldots&\ldots \end{array} \right)$$

　　　　3）$$\pi(j) = \sum\limits_{i=0}^{\infty}\pi(i)P_{ij}$$

　　　　4) $\pi$是方程$\pi P = \pi$的唯一非负解，其中：$$\pi = [\pi(1),\pi(2),...,\pi(j),...]\;\; \sum\limits_{i=0}^{\infty}\pi(i) = 1$$

　　　　上面的性质中需要解释的有：

　　　　1）非周期的马尔科夫链：这个主要是指马尔科夫链的状态转化不是循环的，如果是循环的则永远不会收敛。幸运的是我们遇到的马尔科夫链一般都是非周期性的。用数学方式表述则是：对于任意某一状态i，d为集合$\{n \mid n \geq 1,P_{ii}^n>0 \}$ 的最大公约数，如果 $d=1$ ，则该状态为非周期的

　　　　2）任何两个状态是连通的：这个指的是从任意一个状态可以通过有限步到达其他的任意一个状态，不会出现条件概率一直为0导致不可达的情况。

　　　　3）马尔科夫链的状态数可以是有限的，也可以是无限的。因此可以用于连续概率分布和离散概率分布。、

　　　　4）$\pi$通常称为马尔科夫链的平稳分布。

3. 基于马尔科夫链采样

　　　　如果我们得到了某个平稳分布所对应的马尔科夫链状态转移矩阵，我们就很容易采用出这个平稳分布的样本集。

　　　　假设我们任意初始的概率分布是$\pi_0(x)$, 经过第一轮马尔科夫链状态转移后的概率分布是$\pi_1(x)$，。。。第i轮的概率分布是$\pi_i(x)$。假设经过n轮后马尔科夫链收敛到我们的平稳分布$\pi(x)$，即：$$\pi_n(x) = \pi_{n+1}(x) = \pi_{n+2}(x) =... = \pi(x)$$

　　　　对于每个分布$\pi_i(x)$，我们有：$$\pi_i(x) = \pi_{i-1}(x)P = \pi_{i-2}(x)P^2 = \pi_{0}(x)P^i$$

　　　　现在我们可以开始采样了，首先，基于初始任意简单概率分布比如高斯分布$\pi_0(x)$采样得到状态值$x_0$，基于条件概率分布$P(x|x_0)$采样状态值$x_1$，一直进行下去，当状态转移进行到一定的次数时，比如到n次时，我们认为此时的采样集$(x_n,x_{n+1},x_{n+2},...)$即是符合我们的平稳分布的对应样本集，可以用来做蒙特卡罗模拟求和了。

　　　　总结下基于马尔科夫链的采样过程：

　　　　1）输入马尔科夫链状态转移矩阵$P$，设定状态转移次数阈值$n_1$，需要的样本个数$n_2$

　　　　2）从任意简单概率分布采样得到初始状态值$x_0$

　　　　3）for $t = 0$ to $n_1 + n_2 -1$: 从条件概率分布$P(x|x_t)$中采样得到样本$x_{t+1}$

　　　　样本集$(x_{n_1}, x_{n_1+1},..., x_{n_1+n_2-1})$即为我们需要的平稳分布对应的样本集。

4. 马尔科夫链采样小结

　　　　如果假定我们可以得到我们需要采样样本的平稳分布所对应的马尔科夫链状态转移矩阵，那么我们就可以用马尔科夫链采样得到我们需要的样本集，进而进行蒙特卡罗模拟。但是一个重要的问题是，随意给定一个平稳分布$\pi$,如何得到它所对应的马尔科夫链状态转移矩阵$P$呢？这是个大问题。我们绕了一圈似乎还是没有解决任意概率分布采样样本集的问题。

　　　　幸运的是，MCMC采样通过迂回的方式解决了上面这个大问题，我们在下一篇来讨论MCMC的采样，以及它的使用改进版采样: M-H采样和Gibbs采样.

（欢迎转载，转载请注明出处。欢迎沟通交流： liujianping-ok@163.com）