[笔记]LR和SVM的相同和不同

之前一篇博客中介绍了Logistics Regression的理论原理：http://www.cnblogs.com/bentuwuying/p/6616680.html。

在大大小小的面试过程中，经常会有这个问题：“请说一下逻辑回归（LR）和支持向量机（SVM）之间的相同点和不同点”。现在整理一下，希望对以后面试机器学习方向的同学有所帮助。

（1）为什么将LR和SVM放在一起来进行比较？

回答这个问题其实就是回答LR和SVM有什么相同点。

第一，LR和SVM都是分类算法。

看到这里很多人就不会认同了，因为在很大一部分人眼里，LR是回归算法。我是非常不赞同这一点的，因为我认为判断一个算法是分类还是回归算法的唯一标准就是样本label的类型，如果label是离散的，就是分类算法，如果label是连续的，就是回归算法。很明显，LR的训练数据的label是“0或者1”，当然是分类算法。其实这样不重要啦，暂且迁就我认为他是分类算法吧，再说了，SVM也可以回归用呢。

第二，如果不考虑核函数，LR和SVM都是线性分类算法，也就是说他们的分类决策面都是线性的。

这里要先说明一点，那就是LR也是可以用核函数的，至于为什么通常在SVM中运用核函数而不在LR中运用，后面讲到他们之间区别的时候会重点分析。总之，原始的LR和SVM都是线性分类器，这也是为什么通常没人问你决策树和LR什么区别，决策树和SVM什么区别，你说一个非线性分类器和一个线性分类器有什么区别？

第三，LR和SVM都是监督学习算法。

这个就不赘述什么是监督学习，什么是半监督学习，什么是非监督学习了。

第四，LR和SVM都是判别模型。

判别模型会生成一个表示P(Y|X)的判别函数（或预测模型），而生成模型先计算联合概率p(Y,X)然后通过贝叶斯公式转化为条件概率。简单来说，在计算判别模型时，不会计算联合概率，而在计算生成模型时，必须先计算联合概率。或者这样理解：生成算法尝试去找到底这个数据是怎么生成的（产生的），然后再对一个信号进行分类。基于你的生成假设，那么那个类别最有可能产生这个信号，这个信号就属于那个类别。判别模型不关心数据是怎么生成的，它只关心信号之间的差别，然后用差别来简单对给定的一个信号进行分类。常见的判别模型有：KNN、SVM、LR，常见的生成模型有：朴素贝叶斯，隐马尔可夫模型。当然，这也是为什么很少有人问你朴素贝叶斯和LR以及朴素贝叶斯和SVM有什么区别（哈哈，废话是不是太多）。

第五，LR和SVM在学术界和工业界都广为人知并且应用广泛。

讲完了LR和SVM的相同点，你是不是也认为有必要将他们进行比较一下了呢？而且比较LR和SVM，是不是比让你比较决策树和LR、决策树和SVM、朴素贝叶斯和LR、朴素贝叶斯和SVM更能考察你的功底呢？

（2）LR和SVM的不同。

第一，本质上是其loss function不同。

逻辑回归的损失函数：

支持向量机的目标函数：

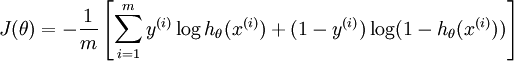
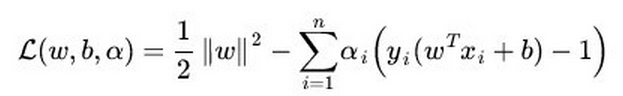
不同的loss function代表了不同的假设前提，也就代表了不同的分类原理，也就代表了一切！！！简单来说，​逻辑回归方法基于概率理论，假设样本为1的概率可以用sigmoid函数来表示，然后通过极大似然估计的方法估计出参数的值，具体细节参考http://blog.csdn.net/pakko/article/details/37878837。支持向量机​基于几何间隔最大化原理，认为存在最大几何间隔的分类面为最优分类面，具体细节参考http://blog.csdn.net/macyang/article/details/38782399

第二，支持向量机只考虑局部的边界线附近的点，而逻辑回归考虑全局（远离的点对边界线的确定也起作用，虽然作用会相对小一些）。

当​你读完上面两个网址的内容，深入了解了LR和SVM的原理过后，会发现影响SVM决策面的样本点只有少数的结构支持向量，当在支持向量外添加或减少任何样本点对分类决策面没有任何影响；而在LR中，每个样本点都会影响决策面的结果。用下图进行说明：

支持向量机改变非支持向量样本并不会引起决策面的变化：

逻辑回归中改变任何样本都会引起决策面的变化：

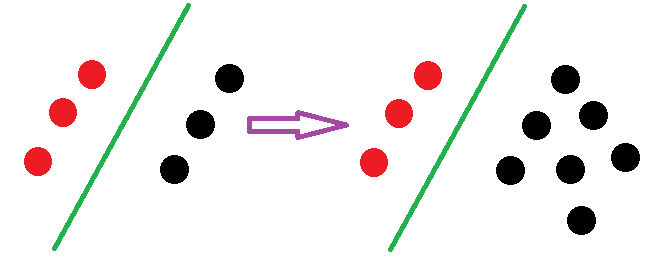
​理解了这一点，有可能你会问，然后呢？有什么用呢？有什么意义吗？对使用两种算法有什么帮助么？一句话回答：

因为上面的原因，得知：线性SVM不直接依赖于数据分布，分类平面不受一类点影响；LR则受所有数据点的影响，如果数据不同类别strongly unbalance，一般需要先对数据做balancing。​（引自http://www.zhihu.com/question/26768865/answer/34078149）

第三，在解决非线性问题时，支持向量机采用核函数的机制，而LR通常不采用核函数的方法。

​这个问题理解起来非常简单。分类模型的结果就是计算决策面，模型训练的过程就是决策面的计算过程。通过上面的第二点不同点可以了解，在计算决策面时，SVM算法里只有少数几个代表支持向量的样本参与了计算，也就是只有少数几个样本需要参与核计算（即kernal machine解的系数是稀疏的）。然而，LR算法里，每个样本点都必须参与决策面的计算过程，也就是说，假设我们在LR里也运用核函数的原理，那么每个样本点都必须参与核计算，这带来的计算复杂度是相当高的。所以，在具体应用时，LR很少运用核函数机制。​

第四，​线性SVM依赖数据表达的距离测度，所以需要对数据先做normalization，LR不受其影响。（引自http://www.zhihu.com/question/26768865/answer/34078149）

一个基于概率，一个基于距离！​

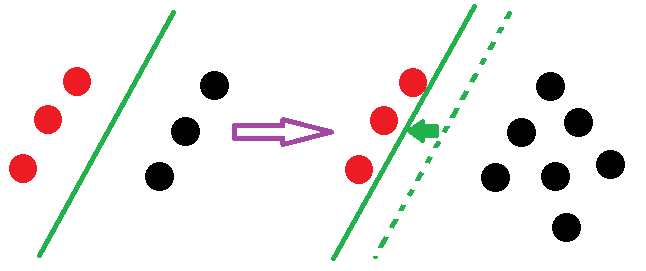
Linear SVM直观上是trade-off两个量
1）a large margin，就是两类之间可以画多宽的gap ；不妨说是正样本应该在分界平面向左gap/2（称正分界），负样本应该在分解平面向右gap/2（称负分界）（见下图）
2）L1 error penalty，对所有不满足上述条件的点做L1 penalty

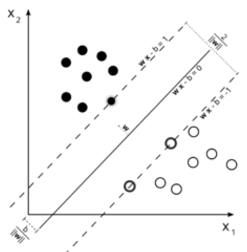
可以看到，给定一个数据集，一旦完成Linear SVM的求解，所有数据点可以被归成两类
1）一类是落在对应分界平面外并被正确分类的点，比如落在正分界左侧的正样本或落在负分界右侧的负样本
2）第二类是落在gap里或被错误分类的点。
假设一个数据集已经被Linear SVM求解，那么往这个数据集里面增加或者删除更多的一类点并不会改变重新求解的Linear SVM平面。这就是它区分与LR的特点，下面我们在看看LR。

值得一提的是求解LR模型过程中，每一个数据点对分类平面都是有影响的，它的影响力远离它到分类平面的距离指数递减。换句话说，LR的解是受数据本身分布影响的。在实际应用中，如果数据维度很高，LR模型都会配合参数的L1 regularization。

要说有什么本质区别，那就是两个模型对数据和参数的敏感程度不同，Linear SVM比较依赖penalty的系数和数据表达空间的测度，而（带正则项的）LR比较依赖对参数做L1 regularization的系数。但是由于他们或多或少都是线性分类器，所以实际上对低维度数据overfitting的能力都比较有限，相比之下对高维度数据，LR的表现会更加稳定，为什么呢？

因为Linear SVM在计算margin有多“宽”的时候是依赖数据表达上的距离测度的，换句话说如果这个测度不好（badly scaled，这种情况在高维数据尤为显著），所求得的所谓Large margin就没有意义了，这个问题即使换用kernel trick（比如用Gaussian kernel）也无法完全避免。所以使用Linear SVM之前一般都需要先对数据做normalization，而求解LR（without regularization）时则不需要或者结果不敏感。（引自http://www.zhihu.com/question/26768865/answer/34078149）

第五，SVM的损失函数就自带正则！！！（损失函数中的1/2||w||^2项），这就是为什么SVM是结构风险最小化算法的原因！！！而LR必须另外在损失函数上添加正则项！！！

以前一直不理解为什么SVM叫做结构风险最小化算法，所谓结构风险最小化，意思就是在训练误差和模型复杂度之间寻求平衡，防止过拟合，从而达到真实误差的最小化。未达到结构风险最小化的目的，最常用的方法就是添加正则项，后面的博客我会具体分析各种正则因子的不同，这里就不扯远了。但是，你发现没，SVM的目标函数里居然自带正则项！！！再看一下上面提到过的SVM目标函数：

SVM目标函数：

​有木有，那不就是L2正则项吗？

不用多说了，如果不明白看看L1正则与L2正则吧，参考http://www.mamicode.com/info-detail-517504.html​。