斐波那契数列Fibonacci问题—动态规划

斐波那契数列定义

Fibonacci array：1,1,2,3,5,8,13,21,34，...

在数学上，斐波那契数列是以递归的方法来定义：

• F(0) = 0
• F(1) = 1
• F(n) = F(n-1) + F(n-2)

用文字描述，就是斐波那契数列由0和1开始，之后的斐波那契系数就是由之前的两数之和想加而得，首几个斐波那契数列系数是：0,1,1,2,3,5,8,13,21,34,55，...特别指出：0不是第一项，而是第零项。

递归解法

最容易想到的解法自然是按照公式的递归解法，具体实现如下：

int fib(int n) {
    if (n < ) return n;
    return fib(n-) + fib(n-);
}

但其实该递归解法会重复两次计算 fib(n-2) 项，时间数量级远远超过 n，是指数级别的增长，时间复杂度很高，如下图所示，更因递归调用占用大量的堆栈空间，对程序而言是一种灾难。所以该种解法如果在面试中肯定是不能让面试官满意的。

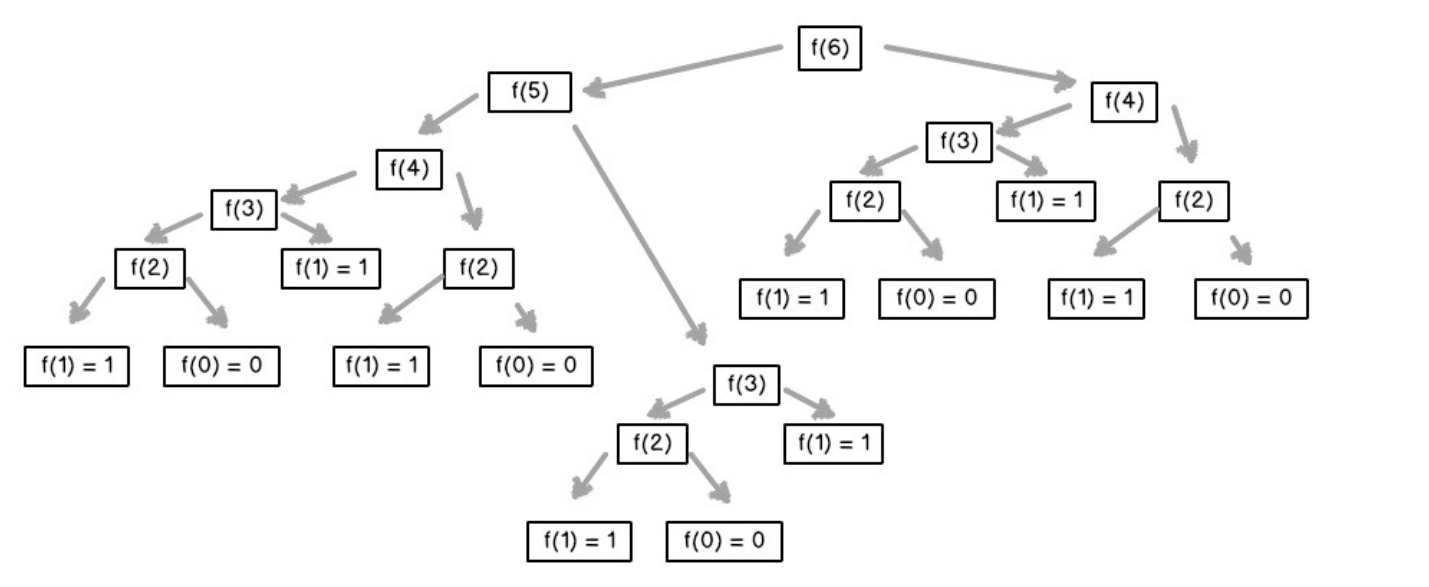
动态规划法

从上图的数据可以看出，递归算法对每个子问题都要重新计算。而实际上，若利用“动态规划”思想这是没必要的。对于已经计算完的子问题，下次再遇到直接使用。将已经计算的结果保存在数组中，在后面直接使用，避免重复计算。具体实现如下：

int fib(int n)
{
    if (n <= ) return n;
    vector<int> mem(n+, -);
    mem[] = ;
    mem[] = ;
    for(int i = ; i <= n; i++){
        mem[i] = mem[i-] + mem[i-];
    }
    return mem[n];
}

上面的这两种解法显然第二种更优，其实第二种解法是利用动态规划改进的算法，算法更简单效率更高。从时间复杂度上看，一般的递归算法是 O(n!)，呈指数级增长，而采用动态规划思想的算法只有 O(n)，但空间复杂度也为 O(n)。

顺序求和法

int fib(int n)
{
    if (n < ) return n;
    int a = ;
    int b = ;
    int c = ;
    for (int i = ; i <= n; ++i) {
        c = a + b;
        a = b;
        b = c;
    }
    return c;
}

该方法是根据 Fibonacci 数列的实际情况在动态规划的算法上改进的方法，不需要保存每一个子问题的结果，只需保存前两个子问题的结果，这样既节省了空间，又达到了动态规规划的效果。按照公式定义前开始的两项 a 和 b 为 0 和 1。后一项 c 是前两项之和，并且 a 和 b重新赋值，动态向右移动，时间复杂度为 O(n)，空间复杂度为 O(1)。这种解法更加优秀！