单调栈求全1（或全0）子矩阵的个数 洛谷P5300与或和 P3400仓鼠窝

　　爆零好爽，被中学生虐好爽，还好我毕业得早

　　求全1（或全0）子矩阵的个数，看了题解有好几种思路，我学了三种，但有两种不是很理解，而且也没另外那个跑得快，所以简单讲述一一下我会的那种来自Caro23333大佬的思路，传送门。

　　首先我们要知道，n*m矩阵的全部子矩阵的个数是C²_n+1*C²_m+1,因为n*m矩阵横的线就有n+1条，竖的线就有m+1条，而我们横的线任选两根，竖的线也任选两根就能组成一个矩阵了。我们求解的思路就是用总的矩阵数去减去不是全0（或者全1）的子矩阵数。那怎么去求出不是全0（或者全1）的子矩阵数？

　　n*m的矩阵，以（n,m）格子作为右下角的子矩阵就有n*m个，因为它的左上角可以在n*m个格子里任意取。现在我们要求不是全0（或者全1）的子矩阵数，那么就是看那些格子作为它的左上角，使得矩阵包含0（或者1）。

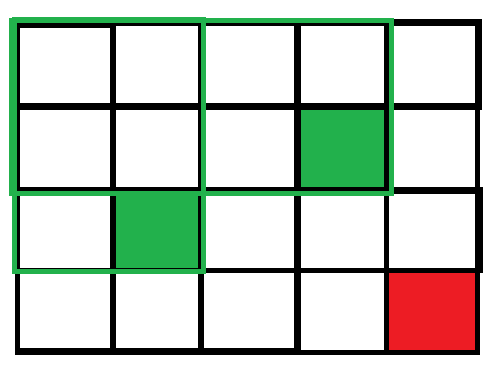
　　就比如上图，假设涂绿色的格子为0，其他全为1，现在我们求以红色格子为右下角，不是全1的子矩阵数。那么我们发现，以绿色区域内的格子作为左上角的子矩阵就不是全1的，因为他们的右下方存在着一个0。而绿色区域也很好求，假设一个绿色点是（x,y）那相应的绿色区域就是x*y。不过我们可以看出，绿色区域会有重复，这样的话会把一个区域算了多遍，那怎么处理这个重复的区域呢？

　　单调栈！我们从上到下，从左到右遍历所有格子，维护maxh[i]为i这一列为0的格子的最大行数，那么我们单调栈维护i,j，i<j有maxa[i]<maxa[j]。严格单调递减的栈，这样的话就使得，当前格子是0的话覆盖的区域不会与前面的重复，因为

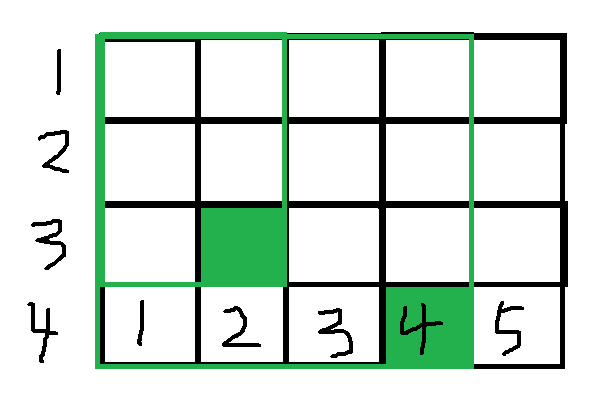
　　当遍历到，（4,4）这个格子的时候，maxh[4]=4，然后栈顶保持的是2，maxh[2]=3，所以把2弹出栈，这时栈顶元素是0，对（4,4）这个右下角产生贡献的绿色区域就是,res[0]+（4-0）*maxh[4]，从图中看就是第二个绿色区域。

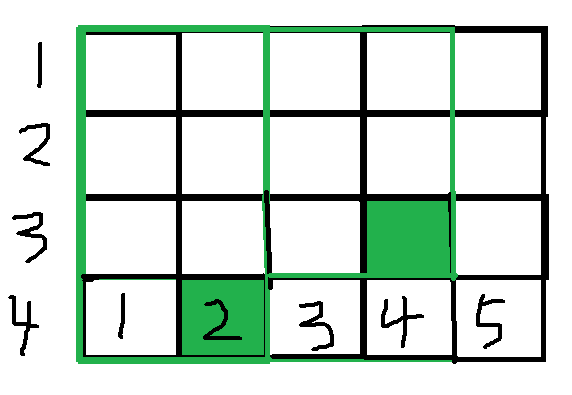
　　而当这个情况时，还是遍历到（4,4）这个格子的时候，maxh[4]=3，然后栈顶保持的是2，maxh[2]=4，所以2不用弹出栈，这时栈顶元素是2，对（4,4）这个右下角产生贡献的绿色区域就是res[2]+（4-2）*maxh[4]。从图中看就是，第一个绿色区域，以及第二个绿色区域不和第一个绿色区域重复的格子数。

　　所以可以知道res是什么了，res[i]就是前i列最下面的那个0能够贡献的格子，也是覆盖的区域，那么res[i]=res[栈顶元素]+（j-栈顶元素）*maxh[i]//相当于宽乘高，当遍历第i行第j列时的res[j]就是(i,j)这个格子作为右下角时，不是全1的子矩阵的左上角个数。

P3400仓鼠窝

 #include<cstdio>
 typedef long long ll;
 const int N=;
 int a[N][N],sta[N],maxh[N];
 ll res[N];
 int main()
 {
     int n,m;
     scanf("%d%d",&n,&m);
     for(int i=;i<=n;i++)
         for(int j=;j<=m;j++)
             scanf("%d",&a[i][j]);
     int top;
     ll all=(1ll*n*(n+)*m*(m+))>>,ans=0ll;//all总的方案数
     for(int i=;i<=n;i++)
     {
         sta[top=]=;
         for(int j=;j<=m;j++)
         {
             if(!a[i][j])//因为我们要求的是全1,所以维护这一列0的最大行数，也就是高度
                 maxh[j]=i;
             while(top&&maxh[sta[top]]<=maxh[j])
                 top--;
             res[j]=res[sta[top]]+1ll*(j-sta[top])*maxh[j];
             ans+=res[j];
             sta[++top]=j;
         }
     }
     printf("%lld\n",all-ans);
     return ;
 }

单调栈哦

P5300 [GXOI/GZOI2019]与或和

　　这题就是把数拆成31位，每一位有对应的权值。

 #include<cstdio>
 typedef long long ll;
 const int N=,mod=;
 int n,cf2[]={},a[N][N],h[N][N];
 int sta[N],maxh[N];
 ll res[N];
 ll count(int k,int x)
 {
     for(int i=;i<=n;i++)
         maxh[i]=;
     int top=;
     ll ans=;
     for(int i=;i<=n;i++)
     {
         sta[top=]=;
         for(int j=;j<=n;j++)
         {
             if(a[i][j]&cf2[k])
                 h[i][j]=x;
             else
                 h[i][j]=x^;
             if(!h[i][j])
                 maxh[j]=i;
             while(top&&maxh[sta[top]]<=maxh[j])
                 top--;
             res[j]=res[sta[top]]+1ll*(j-sta[top])*maxh[j];
             if(res[j]>=mod)
                 res[j]-=mod;
             ans+=res[j];
             if(ans>=mod)
                 ans-=mod;
             sta[++top]=j;
         }
     }
     return ans;
 }
 int main()
 {
     for(int i=;i<=;i++)
         cf2[i]=cf2[i-]<<;
     scanf("%d",&n);
     for(int i=;i<=n;i++)
         for(int j=;j<=n;j++)
             scanf("%d",&a[i][j]);
     ll all=((1ll*n*(n+)*n*(n+))>>)%mod;
     ll ans1=,ans2=;
     for(int k=;k<=;k++)
     {
         ans1+=((all-count(k,)+mod)%mod)*1ll*cf2[k];
         if(ans1>=mod)
             ans1%=mod;
         ans2+=count(k,)*1ll*cf2[k];
         if(ans2>=mod)
             ans2%=mod;
     }
     printf("%lld %lld\n",ans1,ans2);
     return ;
 }

单调栈哦哦