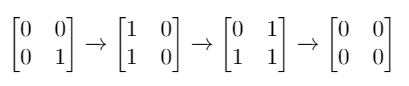【leetcode】1284. Minimum Number of Flips to Convert Binary Matrix to Zero Matrix
题目如下:
Given a
m x nbinary matrixmat. In one step, you can choose one cell and flip it and all the four neighbours of it if they exist (Flip is changing 1 to 0 and 0 to 1). A pair of cells are called neighboors if they share one edge.Return the minimum number of steps required to convert
matto a zero matrix or -1 if you cannot.Binary matrix is a matrix with all cells equal to 0 or 1 only.
Zero matrix is a matrix with all cells equal to 0.
Example 1:
Input: mat = [[0,0],[0,1]]
Output: 3
Explanation: One possible solution is to flip (1, 0) then (0, 1) and finally (1, 1) as shown.Example 2:
Input: mat = [[0]]
Output: 0
Explanation: Given matrix is a zero matrix. We don't need to change it.Example 3:
Input: mat = [[1,1,1],[1,0,1],[0,0,0]]
Output: 6Example 4:
Input: mat = [[1,0,0],[1,0,0]]
Output: -1
Explanation: Given matrix can't be a zero matrixConstraints:
m == mat.lengthn == mat[0].length1 <= m <= 31 <= n <= 3mat[i][j]is 0 or 1.
解题思路:最大就是3*3的矩阵,BFS把每种情况都试一遍就好了。
代码如下:
class Solution(object):
def minFlips(self, mat):
"""
:type mat: List[List[int]]
:rtype: int
"""
import copy
def isAllZero(grid):
count = 0
for i in grid:
count += sum(i)
return count == 0 def encode(grid):
grid_s = ''
for i in range(len(grid)):
for j in range(len(grid[i])):
grid_s += str(grid[i][j])
if i != len(grid) - 1 : grid_s += '#'
return grid_s
def decode(grid_s):
gl = grid_s.split('#')
grid = []
for i in gl:
tl = []
for j in list(i):
tl.append(int(j))
grid.append(tl)
return grid res = float('inf')
queue = [(encode(mat),0)]
dic = {}
dic[encode(mat)] = 0 while len(queue) > 0:
gs,step = queue.pop(0)
grid = decode(gs)
if isAllZero(grid):
res = min(res,step)
continue
elif res <= step:
continue
for i in range(len(grid)):
for j in range(len(grid[i])):
#if grid[i][j] == 0: continue
new_grid = copy.deepcopy(grid)
if new_grid[i][j] == 1:
new_grid[i][j] = 0
else:new_grid[i][j] = 1
directions = [(1, 0), (-1, 0), (0, 1), (0, -1)]
for (x, y) in directions:
if x + i >= 0 and x + i < len(grid) and y + j >= 0 and y + j < len(grid[0]):
if new_grid[x + i][y + j] == 0:
new_grid[x + i][y + j] = 1
else:
new_grid[x + i][y + j] = 0
encode_Str = encode(new_grid)
if encode_Str not in dic or dic[encode_Str] > step + 1:
queue.append((encode(new_grid), step + 1))
dic[encode_Str] = step + 1
return res if res != float('inf') else -1
【leetcode】1284. Minimum Number of Flips to Convert Binary Matrix to Zero Matrix的更多相关文章
- LeetCode 1284. Minimum Number of Flips to Convert Binary Matrix to Zero Matrix (最少翻转次数将二进制矩阵全部置为0)
给一个矩阵mat,每个格子都是0或1,翻转一个格子会将该格子以及相邻的格子(有共同边)全部翻转(0变为1,1变为0) 求问最少需要翻转几次将所有格子全部置为0. 这题的重点是数据范围,比赛结束看了眼数 ...
- 【LeetCode】452. Minimum Number of Arrows to Burst Balloons 解题报告(Python)
[LeetCode]452. Minimum Number of Arrows to Burst Balloons 解题报告(Python) 标签(空格分隔): LeetCode 题目地址:https ...
- 【leetcode】995. Minimum Number of K Consecutive Bit Flips
题目如下: In an array A containing only 0s and 1s, a K-bit flip consists of choosing a (contiguous) suba ...
- 【LeetCode】871. Minimum Number of Refueling Stops 解题报告(Python)
作者: 负雪明烛 id: fuxuemingzhu 个人博客: http://fuxuemingzhu.cn/ 目录 题目描述 题目大意 解题方法 贪心算法 日期 题目地址:https://leetc ...
- 【leetcode】452. Minimum Number of Arrows to Burst Balloons
题目如下: 解题思路:本题可以采用贪心算法.首先把balloons数组按end从小到大排序,然后让第一个arrow的值等于第一个元素的end,依次遍历数组,如果arrow不在当前元素的start到en ...
- 【LeetCode】762. Prime Number of Set Bits in Binary Representation 解题报告(Python)
作者: 负雪明烛 id: fuxuemingzhu 个人博客: http://fuxuemingzhu.cn/ 目录 题目描述 题目大意 解题方法 遍历数字+质数判断 日期 题目地址:https:// ...
- 【leetcode】963. Minimum Area Rectangle II
题目如下: Given a set of points in the xy-plane, determine the minimum area of any rectangle formed from ...
- 【LeetCode】375. Guess Number Higher or Lower II 解题报告(Python)
[LeetCode]375. Guess Number Higher or Lower II 解题报告(Python) 作者: 负雪明烛 id: fuxuemingzhu 个人博客: http://f ...
- 【LeetCode】137. Single Number II 解题报告(Python)
[LeetCode]137. Single Number II 解题报告(Python) 标签: LeetCode 题目地址:https://leetcode.com/problems/single- ...
随机推荐
- Oracle - 子查询、TOP - N
1 子查询 sql 中查询是可以嵌套的,一个查询的结果可以作为另外一个查询的条件.表. SELECT select_list FROM table WHERE expr operator (SELEC ...
- kettle 创建作业发送邮件
1.创建作业 . 2. 发送邮件配置,测试邮件 发件地址可以使用的QQ.126.163等邮箱 smtp server的填写smtp.qq.com或者smtp.126.com等等都可以这里我用Q163邮 ...
- Hadoop集群搭建-03编译安装hadoop
Hadoop集群搭建-05安装配置YARN Hadoop集群搭建-04安装配置HDFS Hadoop集群搭建-03编译安装hadoop Hadoop集群搭建-02安装配置Zookeeper Hado ...
- Phython-守护线程
import threading,time def run(n): print("task is ",n) time.sleep(2) print("task done& ...
- 【div】给div添加滚动条
<div class="infomation" style=" max-height: 500px; overflow: auto;"> style ...
- [C#.net]C#如何解析json文本文件
C#解析Json字符串,可以借助Newtonsoft.Json将Json字符串序列化为对象,再从对象中获取值 Newtonsoft.Json.JsonConvert.DeserializeObject ...
- 修改NPM默认全局安装路径
场景: 最近在新电脑上鼓捣完环境后,打算切换下源,结果使用全局安装的nrm时提示找不到命令,之前都是这么用现在怎么不行了呢? 排查过程: 于是各种折腾,发现- g安装的插件目录在C盘中的某个路径中,后 ...
- QPushButton样式
QPushButton:hover:!pressed { border: 1px solid #434E7A; }
- MySQL导出数据到文件中
一.导出一张表数据 把test_time表中的数据导出成txt 文件 mysql> show global variables like '%secure%'; +--------------- ...
- Java学习笔记【三、运算符、表达式、语句】
运算符 算数运算符 /* / % ++ -- 关系运算符 == != > /< >= /<= 位运算符 &(按位与,有0是0,否则1) |(按位或,有1是1,否则0) ...