Leetcode题目62.不同路径（动态规划-中等）

题目描述：

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

问总共有多少条不同的路径？

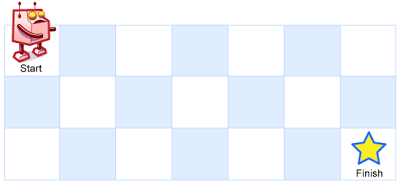
例如，上图是一个7 x 3 的网格。有多少可能的路径？

说明：m 和 n 的值均不超过 100。

示例 1:

输入: m = 3, n = 2
输出: 3
解释:
从左上角开始，总共有 3 条路径可以到达右下角。
1. 向右 -> 向右 -> 向下
2. 向右 -> 向下 -> 向右
3. 向下 -> 向右 -> 向右
示例 2:

输入: m = 7, n = 3
输出: 28

题目解析：

思路一：排列组合

因为机器到底右下角，向下几步，向右几步都是固定的，

比如，m=3, n=2，我们只要向下 1 步，向右 2 步就一定能到达终点。即C(m-1,m+n-2)或者C(n-1,m+n-2);

思路二：动态规划

我们令 dp[i][j] 是到达 i, j 最多路径

动态方程：dp[i][j] = dp[i-1][j] + dp[i][j-1]

注意，对于第一行 dp[0][j](0<=j<=n-1)，或者第一列 dp[i][0](0<=i<=m-1)，由于都是在边界，所以只能为 1

代码实现:

    public static int uniquePaths(int m, int n) {

        int[][] dp = new int[m][n];
        for (int i = 0; i < m; i++) {
            dp[i][0] = 1;
        }
        for (int j = 0; j < n; j++) {
            dp[0][j] = 1;
        }
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }
        return dp[m - 1][n - 1];
    }

时间复杂度：O(m*n)

空间复杂度：O(m*n)

优化空间复杂度：由O(m*n)->O(n)，时间复杂度还是O(m*n)

先初始化一个下面这样的表格，然后用左边的值加上上边的值就可以了

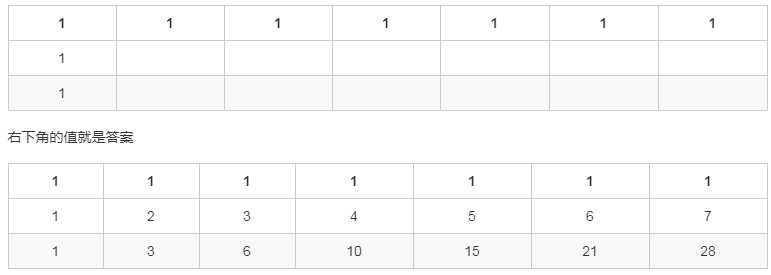
代码实现：

    public static int uniquePaths(int m, int n) {

        int arr[] = new int[n];

        //填充数组arr
        Arrays.fill(arr,1);
        for(int i=1;i<m;i++){
            for(int j=1;j<n;j++){
                arr[j]+=arr[j-1];
            }
        }
        return arr[n-1];
    }