sklearn逻辑回归实战
题目要求
根据学生两门课的成绩和是否入学的数据，预测学生能否顺利入学：利用ex2data1.txt和ex2data2.txt中的数据，进行逻辑回归和预测。
数据放在最后边。
ex2data1.txt处理
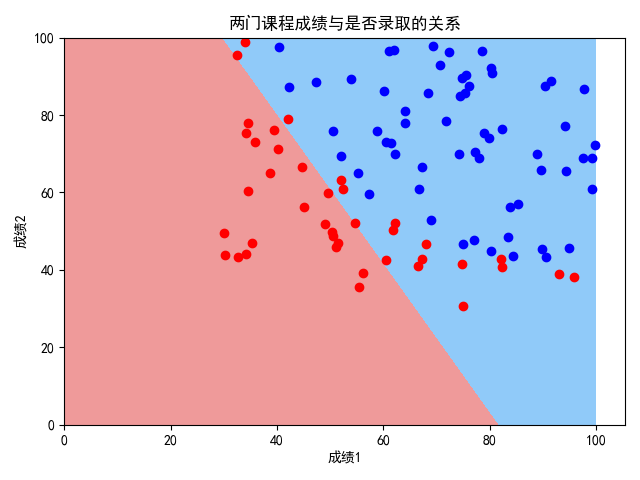
作散点图可知，决策大致符合线性关系，但还是有弯曲（非线性），用线性效果并不好，因此可用两种方案：方案一，无多项式特征；方案二，有多项式特征。
方案一：无多项式特征
对ex2data1.txt中的数据进行逻辑回归，无多项式特征
代码实现如下：
"""
对ex2data1.txt中的数据进行逻辑回归（无多项式特征）
"""
from sklearn.model_selection import train_test_split
from matplotlib.colors import ListedColormap
from sklearn.linear_model import LogisticRegression
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
# 数据格式：成绩1,成绩2,是否被录取（1代表被录取，0代表未被录取）
# 函数（画决策边界）定义
def plot_decision_boundary(model, axis):
x0, x1 = np.meshgrid(
np.linspace(axis[0], axis[1], int((axis[1] - axis[0]) * 100)).reshape(-1, 1),
np.linspace(axis[2], axis[3], int((axis[3] - axis[2]) * 100)).reshape(-1, 1),
)
X_new = np.c_[x0.ravel(), x1.ravel()]
y_predict = model.predict(X_new)
zz = y_predict.reshape(x0.shape)
custom_cmap = ListedColormap(['#EF9A9A', '#FFF59D', '#90CAF9'])
plt.contourf(x0, x1, zz, cmap=custom_cmap)
# 读取数据
data = np.loadtxt('ex2data1.txt', delimiter=',')
data_X = data[:, 0:2]
data_y = data[:, 2]
# 数据分割
X_train, X_test, y_train, y_test = train_test_split(data_X, data_y, random_state=666)
# 训练模型
log_reg = LogisticRegression()
log_reg.fit(X_train, y_train)
# 结果可视化
plot_decision_boundary(log_reg, axis=[0, 100, 0, 100])
plt.scatter(data_X[data_y == 0, 0], data_X[data_y == 0, 1], color='red')
plt.scatter(data_X[data_y == 1, 0], data_X[data_y == 1, 1], color='blue')
plt.xlabel('成绩1')
plt.ylabel('成绩2')
plt.title('两门课程成绩与是否录取的关系')
plt.show()
# 模型测试
print(log_reg.score(X_train, y_train))
print(log_reg.score(X_test, y_test))
输出结果如下：
0.8533333333333334
0.76
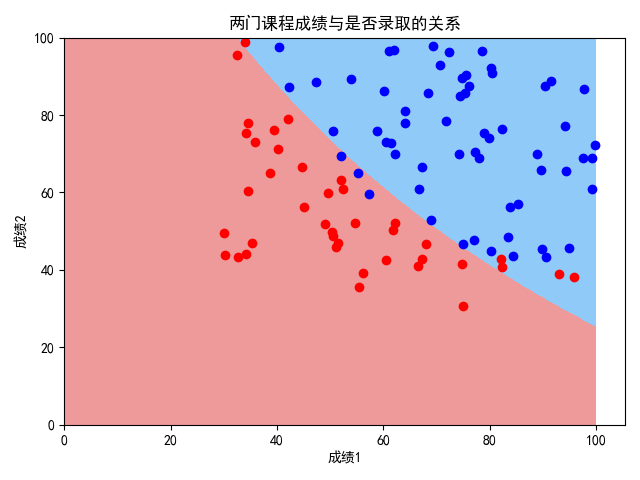
方案二：引入多项式特征
对ex2data1.txt中的数据进行逻辑回归，引入多项式特征。经调试，当degree为3时，耗费时间较长；当degree为2时，耗费时间可接受，效果与方案一相比好了很多
实现如下：
"""
对ex2data1.txt中的数据进行逻辑回归（引入多项式特征）
"""
from sklearn.model_selection import train_test_split
from matplotlib.colors import ListedColormap
from sklearn.linear_model import LogisticRegression
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
# 数据格式：成绩1,成绩2,是否被录取（1代表被录取，0代表未被录取）
# 函数定义
def plot_decision_boundary(model, axis):
x0, x1 = np.meshgrid(
np.linspace(axis[0], axis[1], int((axis[1] - axis[0]) * 100)).reshape(-1, 1),
np.linspace(axis[2], axis[3], int((axis[3] - axis[2]) * 100)).reshape(-1, 1),
)
X_new = np.c_[x0.ravel(), x1.ravel()]
y_predict = model.predict(X_new)
zz = y_predict.reshape(x0.shape)
custom_cmap = ListedColormap(['#EF9A9A', '#FFF59D', '#90CAF9'])
plt.contourf(x0, x1, zz, cmap=custom_cmap)
def PolynomialLogisticRegression(degree):
return Pipeline([
('poly', PolynomialFeatures(degree=degree)),
('std_scaler', StandardScaler()),
('log_reg', LogisticRegression())
])
# 读取数据
data = np.loadtxt('ex2data1.txt', delimiter=',')
data_X = data[:, 0:2]
data_y = data[:, 2]
# 数据分割
X_train, X_test, y_train, y_test = train_test_split(data_X, data_y, random_state=666)
# 训练模型
poly_log_reg = PolynomialLogisticRegression(degree=2)
poly_log_reg.fit(X_train, y_train)
# 结果可视化
plot_decision_boundary(poly_log_reg, axis=[0, 100, 0, 100])
plt.scatter(data_X[data_y == 0, 0], data_X[data_y == 0, 1], color='red')
plt.scatter(data_X[data_y == 1, 0], data_X[data_y == 1, 1], color='blue')
plt.xlabel('成绩1')
plt.ylabel('成绩2')
plt.title('两门课程成绩与是否录取的关系')
plt.show()
# 模型测试
print(poly_log_reg.score(X_train, y_train))
print(poly_log_reg.score(X_test, y_test))
输出如下：
0.92
0.92
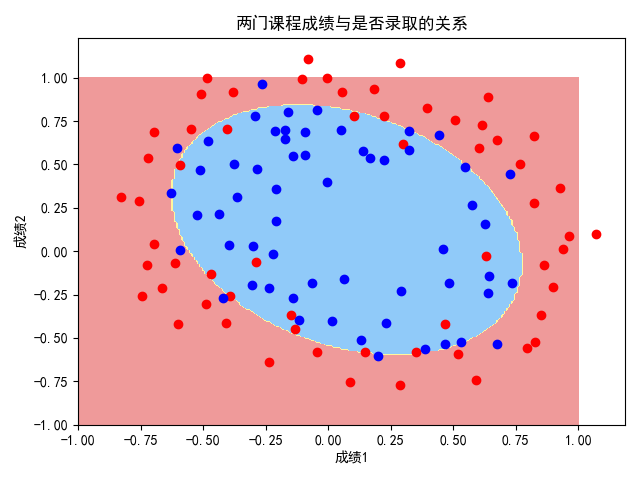
ex2data2.txt处理
作散点图可知，这组数据的决策边界绝对是非线性的，所以直接引入多项式特征对ex2data2.txt中的数据进行逻辑回归。
代码实现如下：
"""
对ex2data2.txt中的数据进行逻辑回归（引入多项式特征）
"""
from sklearn.model_selection import train_test_split
from matplotlib.colors import ListedColormap
from sklearn.linear_model import LogisticRegression
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
# 数据格式：成绩1,成绩2,是否被录取（1代表被录取，0代表未被录取）
# 函数定义
def plot_decision_boundary(model, axis):
x0, x1 = np.meshgrid(
np.linspace(axis[0], axis[1], int((axis[1] - axis[0]) * 100)).reshape(-1, 1),
np.linspace(axis[2], axis[3], int((axis[3] - axis[2]) * 100)).reshape(-1, 1),
)
X_new = np.c_[x0.ravel(), x1.ravel()]
y_predict = model.predict(X_new)
zz = y_predict.reshape(x0.shape)
custom_cmap = ListedColormap(['#EF9A9A', '#FFF59D', '#90CAF9'])
plt.contourf(x0, x1, zz, cmap=custom_cmap)
def PolynomialLogisticRegression(degree):
return Pipeline([
('poly', PolynomialFeatures(degree=degree)),
('std_scaler', StandardScaler()),
('log_reg', LogisticRegression())
])
# 读取数据
data = np.loadtxt('ex2data2.txt', delimiter=',')
data_X = data[:, 0:2]
data_y = data[:, 2]
# 数据分割
X_train, X_test, y_train, y_test = train_test_split(data_X, data_y, random_state=666)
# 训练模型
poly_log_reg = PolynomialLogisticRegression(degree=2)
poly_log_reg.fit(X_train, y_train)
# 结果可视化
plot_decision_boundary(poly_log_reg, axis=[-1, 1, -1, 1])
plt.scatter(data_X[data_y == 0, 0], data_X[data_y == 0, 1], color='red')
plt.scatter(data_X[data_y == 1, 0], data_X[data_y == 1, 1], color='blue')
plt.xlabel('成绩1')
plt.ylabel('成绩2')
plt.title('两门课程成绩与是否录取的关系')
plt.show()
# 模型测试
print(poly_log_reg.score(X_train, y_train))
print(poly_log_reg.score(X_test, y_test))
输出结果如下：
由图可知，分类结果较好。
0.7954545454545454
0.9
两份数据
ex2data1.txt
34.62365962451697,78.0246928153624,0
30.28671076822607,43.89499752400101,0
35.84740876993872,72.90219802708364,0
60.18259938620976,86.30855209546826,1
79.0327360507101,75.3443764369103,1
45.08327747668339,56.3163717815305,0
61.10666453684766,96.51142588489624,1
75.02474556738889,46.55401354116538,1
76.09878670226257,87.42056971926803,1
84.43281996120035,43.53339331072109,1
95.86155507093572,38.22527805795094,0
75.01365838958247,30.60326323428011,0
82.30705337399482,76.48196330235604,1
69.36458875970939,97.71869196188608,1
39.53833914367223,76.03681085115882,0
53.9710521485623,89.20735013750205,1
69.07014406283025,52.74046973016765,1
67.94685547711617,46.67857410673128,0
70.66150955499435,92.92713789364831,1
76.97878372747498,47.57596364975532,1
67.37202754570876,42.83843832029179,0
89.67677575072079,65.79936592745237,1
50.534788289883,48.85581152764205,0
34.21206097786789,44.20952859866288,0
77.9240914545704,68.9723599933059,1
62.27101367004632,69.95445795447587,1
80.1901807509566,44.82162893218353,1
93.114388797442,38.80067033713209,0
61.83020602312595,50.25610789244621,0
38.78580379679423,64.99568095539578,0
61.379289447425,72.80788731317097,1
85.40451939411645,57.05198397627122,1
52.10797973193984,63.12762376881715,0
52.04540476831827,69.43286012045222,1
40.23689373545111,71.16774802184875,0
54.63510555424817,52.21388588061123,0
33.91550010906887,98.86943574220611,0
64.17698887494485,80.90806058670817,1
74.78925295941542,41.57341522824434,0
34.1836400264419,75.2377203360134,0
83.90239366249155,56.30804621605327,1
51.54772026906181,46.85629026349976,0
94.44336776917852,65.56892160559052,1
82.36875375713919,40.61825515970618,0
51.04775177128865,45.82270145776001,0
62.22267576120188,52.06099194836679,0
77.19303492601364,70.45820000180959,1
97.77159928000232,86.7278223300282,1
62.07306379667647,96.76882412413983,1
91.56497449807442,88.69629254546599,1
79.94481794066932,74.16311935043758,1
99.2725269292572,60.99903099844988,1
90.54671411399852,43.39060180650027,1
34.52451385320009,60.39634245837173,0
50.2864961189907,49.80453881323059,0
49.58667721632031,59.80895099453265,0
97.64563396007767,68.86157272420604,1
32.57720016809309,95.59854761387875,0
74.24869136721598,69.82457122657193,1
71.79646205863379,78.45356224515052,1
75.3956114656803,85.75993667331619,1
35.28611281526193,47.02051394723416,0
56.25381749711624,39.26147251058019,0
30.05882244669796,49.59297386723685,0
44.66826172480893,66.45008614558913,0
66.56089447242954,41.09209807936973,0
40.45755098375164,97.53518548909936,1
49.07256321908844,51.88321182073966,0
80.27957401466998,92.11606081344084,1
66.74671856944039,60.99139402740988,1
32.72283304060323,43.30717306430063,0
64.0393204150601,78.03168802018232,1
72.34649422579923,96.22759296761404,1
60.45788573918959,73.09499809758037,1
58.84095621726802,75.85844831279042,1
99.82785779692128,72.36925193383885,1
47.26426910848174,88.47586499559782,1
50.45815980285988,75.80985952982456,1
60.45555629271532,42.50840943572217,0
82.22666157785568,42.71987853716458,0
88.9138964166533,69.80378889835472,1
94.83450672430196,45.69430680250754,1
67.31925746917527,66.58935317747915,1
57.23870631569862,59.51428198012956,1
80.36675600171273,90.96014789746954,1
68.46852178591112,85.59430710452014,1
42.0754545384731,78.84478600148043,0
75.47770200533905,90.42453899753964,1
78.63542434898018,96.64742716885644,1
52.34800398794107,60.76950525602592,0
94.09433112516793,77.15910509073893,1
90.44855097096364,87.50879176484702,1
55.48216114069585,35.57070347228866,0
74.49269241843041,84.84513684930135,1
89.84580670720979,45.35828361091658,1
83.48916274498238,48.38028579728175,1
42.2617008099817,87.10385094025457,1
99.31500880510394,68.77540947206617,1
55.34001756003703,64.9319380069486,1
74.77589300092767,89.52981289513276,1
ex2data2.txt
0.051267,0.69956,1
-0.092742,0.68494,1
-0.21371,0.69225,1
-0.375,0.50219,1
-0.51325,0.46564,1
-0.52477,0.2098,1
-0.39804,0.034357,1
-0.30588,-0.19225,1
0.016705,-0.40424,1
0.13191,-0.51389,1
0.38537,-0.56506,1
0.52938,-0.5212,1
0.63882,-0.24342,1
0.73675,-0.18494,1
0.54666,0.48757,1
0.322,0.5826,1
0.16647,0.53874,1
-0.046659,0.81652,1
-0.17339,0.69956,1
-0.47869,0.63377,1
-0.60541,0.59722,1
-0.62846,0.33406,1
-0.59389,0.005117,1
-0.42108,-0.27266,1
-0.11578,-0.39693,1
0.20104,-0.60161,1
0.46601,-0.53582,1
0.67339,-0.53582,1
-0.13882,0.54605,1
-0.29435,0.77997,1
-0.26555,0.96272,1
-0.16187,0.8019,1
-0.17339,0.64839,1
-0.28283,0.47295,1
-0.36348,0.31213,1
-0.30012,0.027047,1
-0.23675,-0.21418,1
-0.06394,-0.18494,1
0.062788,-0.16301,1
0.22984,-0.41155,1
0.2932,-0.2288,1
0.48329,-0.18494,1
0.64459,-0.14108,1
0.46025,0.012427,1
0.6273,0.15863,1
0.57546,0.26827,1
0.72523,0.44371,1
0.22408,0.52412,1
0.44297,0.67032,1
0.322,0.69225,1
0.13767,0.57529,1
-0.0063364,0.39985,1
-0.092742,0.55336,1
-0.20795,0.35599,1
-0.20795,0.17325,1
-0.43836,0.21711,1
-0.21947,-0.016813,1
-0.13882,-0.27266,1
0.18376,0.93348,0
0.22408,0.77997,0
0.29896,0.61915,0
0.50634,0.75804,0
0.61578,0.7288,0
0.60426,0.59722,0
0.76555,0.50219,0
0.92684,0.3633,0
0.82316,0.27558,0
0.96141,0.085526,0
0.93836,0.012427,0
0.86348,-0.082602,0
0.89804,-0.20687,0
0.85196,-0.36769,0
0.82892,-0.5212,0
0.79435,-0.55775,0
0.59274,-0.7405,0
0.51786,-0.5943,0
0.46601,-0.41886,0
0.35081,-0.57968,0
0.28744,-0.76974,0
0.085829,-0.75512,0
0.14919,-0.57968,0
-0.13306,-0.4481,0
-0.40956,-0.41155,0
-0.39228,-0.25804,0
-0.74366,-0.25804,0
-0.69758,0.041667,0
-0.75518,0.2902,0
-0.69758,0.68494,0
-0.4038,0.70687,0
-0.38076,0.91886,0
-0.50749,0.90424,0
-0.54781,0.70687,0
0.10311,0.77997,0
0.057028,0.91886,0
-0.10426,0.99196,0
-0.081221,1.1089,0
0.28744,1.087,0
0.39689,0.82383,0
0.63882,0.88962,0
0.82316,0.66301,0
0.67339,0.64108,0
1.0709,0.10015,0
-0.046659,-0.57968,0
-0.23675,-0.63816,0
-0.15035,-0.36769,0
-0.49021,-0.3019,0
-0.46717,-0.13377,0
-0.28859,-0.060673,0
-0.61118,-0.067982,0
-0.66302,-0.21418,0
-0.59965,-0.41886,0
-0.72638,-0.082602,0
-0.83007,0.31213,0
-0.72062,0.53874,0
-0.59389,0.49488,0
-0.48445,0.99927,0
-0.0063364,0.99927,0
0.63265,-0.030612,0
作者：@臭咸鱼
转载请注明出处：https://www.cnblogs.com/chouxianyu/
欢迎讨论和交流!
sklearn逻辑回归实战的更多相关文章
- 通俗地说逻辑回归【Logistic regression】算法（二）sklearn逻辑回归实战
前情提要: 通俗地说逻辑回归[Logistic regression]算法(一) 逻辑回归模型原理介绍 上一篇主要介绍了逻辑回归中,相对理论化的知识,这次主要是对上篇做一点点补充,以及介绍sklear ...
- sklearn逻辑回归(Logistic Regression,LR)调参指南
python信用评分卡建模(附代码,博主录制) https://study.163.com/course/introduction.htm?courseId=1005214003&utm_ca ...
- sklearn逻辑回归
sklearn逻辑回归 logistics回归名字虽然叫回归,但实际是用回归方法解决分类的问题,其形式简洁明了,训练的模型参数还有实际的解释意义,因此在机器学习中非常常见. 理论部分 设数据集有n个独 ...
- sklearn逻辑回归(Logistic Regression)类库总结
class sklearn.linear_model.LogisticRegression(penalty=’l2’, dual=False, tol=0.0001, C=1.0, fit_inter ...
- sklearn逻辑回归库函数直接拟合数据
from sklearn import model_selection from sklearn.linear_model import LogisticRegression from sklearn ...
- 机器学习入门-概率阈值的逻辑回归对准确度和召回率的影响 lr.predict_proba(获得预测样本的概率值)
1.lr.predict_proba(under_text_x) 获得的是正负的概率值 在sklearn逻辑回归的计算过程中,使用的是大于0.5的是正值,小于0.5的是负值,我们使用使用不同的概率结 ...
- 逻辑回归原理_挑战者飞船事故和乳腺癌案例_Python和R_信用评分卡（AAA推荐）
sklearn实战-乳腺癌细胞数据挖掘(博客主亲自录制视频教程) https://study.163.com/course/introduction.htm?courseId=1005269003&a ...
- 逻辑回归--美国挑战者号飞船事故_同盾分数与多头借贷Python建模实战
python信用评分卡(附代码,博主录制) https://study.163.com/course/introduction.htm?courseId=1005214003&utm_camp ...
- 机器学习_线性回归和逻辑回归_案例实战：Python实现逻辑回归与梯度下降策略_项目实战：使用逻辑回归判断信用卡欺诈检测
线性回归: 注:为偏置项,这一项的x的值假设为[1,1,1,1,1....] 注:为使似然函数越大,则需要最小二乘法函数越小越好 线性回归中为什么选用平方和作为误差函数?假设模型结果与测量值 误差满足 ...
随机推荐
- 【数据库开发】MySQL命令大全
1.连接Mysql 格式: mysql -h主机地址 -u用户名 -p用户密码1.连接到本机上的MYSQL. 首先打开DOS窗口,然后进入目录mysql\bin,再键入命令mysql -u root ...
- 为何我的网站http总是跳转https？能不能让http不跳转https？谈谈我遇到的坑和解决方案。
如题,突然想给我的个人网站加一个ssl,让它能够通过https访问. 但一顿操作猛如虎后,发现只能https访问了,手动输入http也会无限跳转到https. 现在说下我的排查思路和解决方案: 1. ...
- 最新 拉卡拉java校招面经 （含整理过的面试题大全）
从6月到10月,经过4个月努力和坚持,自己有幸拿到了网易雷火.京东.去哪儿.拉卡拉等10家互联网公司的校招Offer,因为某些自身原因最终选择了拉卡拉.6.7月主要是做系统复习.项目复盘.LeetCo ...
- JSP入门基础知识详细版（通俗易懂）
JSP 第一篇: 概述.原理.周期.指令.行为.内置对象.JavaBean (一) JSP概述以及简单使用 什么是JSP? JSP全名为Java Server Pages,java服务器页面.JSP是 ...
- centos7配置hadoop
hadoop压缩包下载: 链接:https://pan.baidu.com/s/1dz0Hh75VNKEebcYcbN-4Hw 提取码:g2e3 java压缩包下载: 链接:https://pan.b ...
- Java的设计模式（3）--工厂模式
工厂模式是定义一个用于创建对象的接口,让子类决定实例化哪一个类.工厂方法使一个类的实例化延迟到子类. 工厂模式涉及四种角色: 抽象产品(Product):抽象类或者接口,负责定义具体产品必须实现的方法 ...
- WebElement的方法：
这个类代表HTML页面元素 id_ #当前元素的ID tag_name #获取元素标签名的属性 text #获取该元素的文本. click() #单击(点击)元素 submit() #提交表单 cle ...
- PCA降维笔记
PCA降维笔记 一个非监督的机器学习算法 主要用于数据的降维 通过降维, 可以发现更便 于人类理解的特征 其他应用:可视化:去噪 PCA(Principal Component Analysis)是一 ...
- go hello world第一个程序
main 函数所在的包名必须使用main import "fmt" 导入包fmt fmt包包含了Println方法的定义 func main() 程序运行入口方法和c语言相似 ...
- C# Enum操作
枚举定义 /// <summary> /// 节点类型 /// </summary> public enum NodeTypeEnum { 企业 = , 人员 = , 人员地址 ...