# N数码问题

N数码问题

首先，先贯彻一个理念。奇偶性很神奇，对于一类问题，如果属于同种性质（奇偶性相同），那么它们就是完全相同（这个在某种意义上说）的，，一些问题如果奇偶性相同那么里面涉及的问题都是等价的。

数码问题考虑的是逆序对的奇偶性。将二维数组排成一维，空格和左右的数交换不改变逆序对个数（实际上在一维中，空格和左右的数交换，忽略空格的话，交换前后一维数组的排列顺序是完全不变的）。

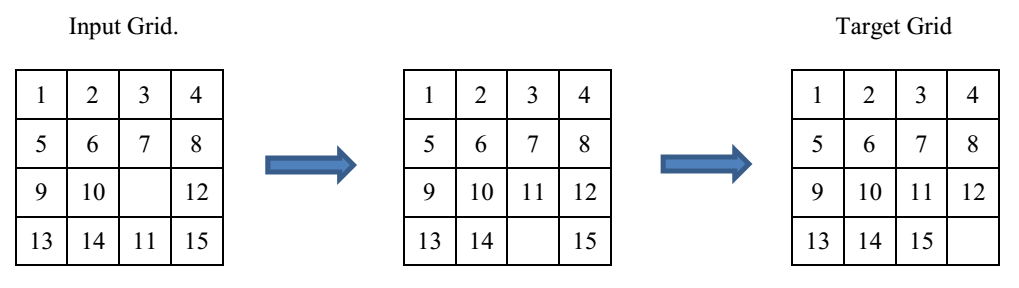
4*4空间

5 6 7 8 \n 9 10 % 12 --> 5 6 % 8 \n 9 10 7 12   空格和上面的数7交换相当于7依次和后面的8 9 10交换共N-1个数。

将7 8 9 10作为一个整体，内部交换不改变外部的逆序对个数（也就是这个整个前后数的逆序对个数）。在这个整体中，8 9 10之间的逆序对个数也是不改变的，会改变的只有7和8 9 10之间的逆序对个数（共形成N-1个逆序对）。

这个整体中，原来是逆序的变成正序，原来正序变成逆序，因此原来逆序对数x+交换后的逆序对数y=N-1;

当N为奇数时，x+y=奇数，x,y一奇一偶，差值为奇数
当N为偶数时，x+y=偶数，x,y同奇偶性，差值为偶数

• 两个不同状态相互可达的充要条件：“ 两个状态逆序对数之差 ” 和 “ 两个状态空格所在行数之差 ” 奇偶性相同。（这里考虑空格所在行数之差是因为，空格只有上下交换才会改变逆序对数）

2019年杭电多校联赛-Just an Old Puzzle

• 15数码是否有解问题

#include <bits/stdc++.h>
using namespace std;
#define fre freopen("C:\\Users\\22765\\Desktop\\in.txt","r",stdin);
#define ms(a) memset((a),0,sizeof(a))
#define rep(i,a,b) for(register int (i)=(a);(i)<(b);++(i))
#define sf(x) scanf("%d",&(x))
#define reg register
typedef long long LL;
const int inf=(0x7f7f7f7f);
const int maxn=3000;
int a[20];

int main(){
	int t;sf(t);
	int x,r;
	while(t--){
		int k=0;
		rep(i,0,4)rep(j,0,4){
			sf(x);
			if(x==0){
				r=i;continue;
			}
			a[k++]=x;
		}
		//计算逆序对可以使用树状数组，这里规模小，直接爆力
		int ni=0;
		rep(i,0,k){
			rep(j,0,i)
			if(a[j]>a[i])ni++;
		}

		if((ni+3-r)&1)puts("No");
		else puts("Yes");
	}
	return 0;
}