EBS GL 日记账行“账户说明”段说明显示不全
问题描述:
路径:总帐管理超级用户/日记帐/输入
如下图所示,日记账行的“账户说明字段”段值说明显示不全

解决方法:
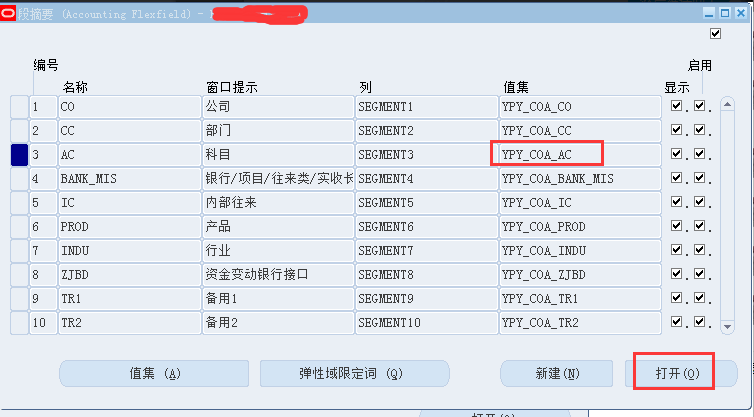
路径:总帐管理超级用户/设置/财务系统/弹性域/关键字/段
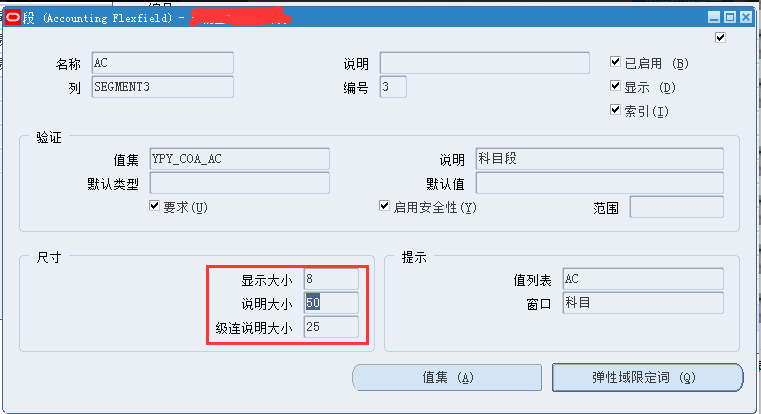
如下图所示,找到相应的弹性域段的值集,修改“级连说明大小”
EBS GL 日记账行“账户说明”段说明显示不全的更多相关文章
- Oracle一列的多行数据拼成一行显示字符
Oracle一列的多行数据拼成一行显示字符 oracle 提供了两个函数WMSYS.WM_CONCAT 和 ListAgg函数. www.2cto.com 先介绍:WMSYS.WM_CO ...
- Easyui Datagrid rownumbers行号四位、五位显示不完全的解决办法
Easyui Datagrid rownumbers行号四位.五位显示不完全的解决办法(引) 方法一: 相信很多人在使用easyui的时候都遇到过这个问题,当我们设置成显示Rownumber的时候,你 ...
- 利用jquery表格添加一行并在每行第一列大写字母显示实现方法
表格添加一行并在每行第一列大写字母显示jquery实现方法 <!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.01 Transitional//EN& ...
- Cell 动态行高文字显示不全问题探索
目录 问题概述 一.新建工程 二.尝试复现问题 尝试解决 修改contentLblBtmCon优先级为High(750) 修改contentLblBtmCon优先级为Low(250) 小结 其他解决思 ...
- EBS WEBADI导入日记账 客户化账户组合规则校验
近期项目需求对EBS中WEBADI导入日记账时,在加载数据时需要对账户组合额外进行客户化的校验,需要能够做到将校验结果体现在WEBADI模板的数据上,并且对每条错误数据都单独报错. 项目上的方案是调整 ...
- Oracle EBS GL 总账日记账打开报错此职责无可用函数
系统管理员下,跑请求:
- Oracle EBS GL 创建会计科目
SELECT ct.trx_number ,l.accounting_class_code ,l.entered_dr ,l.entered_cr ,fnd_flex_ext.get_segs('SQ ...
- Oracle EBS GL 会计科目报错 GL_ACCESS_SET_LEDGERS
1.会计科目设置后,总账中找不到对应账簿 2.原因是新版本系统物化视图有问题,参照metalink解决方案得知原路径 ...
- Oracle EBS GL总账凭证取值
SELECT gh.je_header_id, gh.period_name, gh.default_effective_date, gh.je_source, gs.user_je_source_n ...
随机推荐
- 8 java 笔记
1 import语句可以简化编程,可以导入指定包下面的某个类或者全部类 2 java.lang,Object类是所有类的父类,要么是其直接父类,要么是其间接父类 3 子类扩展了父类,子类是一种特殊的父 ...
- ChinaCock扫描控件介绍-使用TCCBarcodeScanner引起app闪退
好几个ChinaCock的朋友说遇到扫码时闪退,进一步总结,都是Android 8的机器上才会出现,今天我也遇到.正好有朋友说,按下面这个改配置文件就可以解决: <!-- 扫描的activity ...
- centos php7 amqp
yum install -y librabbitmq-devel /home/git/php/bin/pecl install amqp echo "extension=amqp.so&qu ...
- fastadmin 隐藏操作栏按钮
formatter: function (value, row, index) { var that = $.extend({}, this); $(table).data({"operat ...
- php 随笔 截取字符串 跳出循环 去除空格 修改上传文件大小限制
substr(string,start,length) echo substr("Hello world",6); world 跳出循环 for($i=1; $i<5; $i ...
- How to mount remote Windows shares
Contents Required packages Basic method Better Method Even-better method Yet Another Even-better m ...
- Windows live Writer Tips
http://lehsys.blogspot.com/2013/03/windows-live-writer-how-to-change.html http://www.carlosag.net/to ...
- Delphi GetCommModemStatus函数
- 第十五章·Kibana深入-Dev Tools及Lucene语法
Dev Tools介绍 Dev Tools 页面包含开发工具,您可以使用这些Dev Tools与Kibana中的数据进行交互. 原先的交互式控制台Sense,使用户方便的通过浏览器直接与Elastic ...
- 生产者消费者问题--BlockingQueue
# 代码: public class App { public static void main(String[] args) { BlockingQueue<Integer> queue ...
