个股和股票池的beta系数的估算
个股的beta系数的估算
代码
def test_gg_beta(symbol='000895.sz',
start='2018-01-01',
plot_price=True,
align_to='gg',
plot_k=True,
):
'''
align_to: str, ['gg', 'dp'], 数据对齐的方式
'gg': 表示对齐到个股, 改变大盘的数据, 以对齐到个股上
'dp': 表示对齐到大盘, 改变个股的数据, 以对齐到大盘上
>>> symbol='000895.sz'
>>> start='2018-01-01'
>>> beta, df = test_gg_beta(align_to='gg', plot_k=False)
>>> beta2, df2 = test_gg_beta(align_to='dp', plot_k=False)
>>> beta, df, plots = test_gg_beta('000933.sz')
>>> beta, df = test_gg_beta('000933.sz', plot_price=False, plot_k=False)
结果是:
0.83(双汇发展 @ 2018年)
1.64(神火股份 @ 2018年)
'''
_date = datetime.datetime.now().date().isoformat()
title='QC图件: 用于计算个股的Beta系数(DP:399317) \n 制作日期: {}'.format(_date)
c=Context(symbol)
stk = Stock(c,start)
stk.grab_data_from_tdxhq()
stk.qfq()
stk.grab_index_from_tdxhq()
stk.indicator()
# 个股通常会有停牌的时候, 所以需要对齐
# 比如以个股为准, 把大盘对齐到个股是时间戳里:
# 将大盘的收盘线, 插入到个股的ohlc数据框里(用assign方法)
if align_to == 'gg':
f = stk.ohlc.close[0] / stk.aindex.close[0]
df=stk.ohlc.assign(dp=stk.aindex.close * f)
df=df.loc[:, ['close', 'dp']]
beta = ttr.estimateBeta(df.close, df.dp)
title += '\n{:s}({:s})的Beta系数: {:.4f}(数据对齐到个股)'.format(stk.context.name,stk.context.code, beta)
if plot_price:
plt.figure()
df.plot(title=title)
elif align_to == 'dp':
f = stk.aindex.close[0] / stk.ohlc.close[0]
df2 = stk.aindex.assign(gg=stk.ohlc.close * f)
df2 = df2.loc[:, ['close', 'gg']]
df2 = df2.fillna(method='ffill') # 向未来填充 (用老数据向下填充)
beta2 = ttr.estimateBeta(df2.gg, df2.close)
title += '\n{:s}({:s})的Beta系数: {:.4f}(数据对齐到大盘)'.format(stk.context.name,stk.context.code, beta2)
if plot_price:
plt.figure()
df2.plot(title=title)
if plot_k:
# fig,ax = plt.subplots(1,1)
#stk.mycandlestick_ohlc(ax, [20,60])
#stk.mycandlestick_ohlc(ax, with_raw_quotes=True)
# stk.mycandlestick_ohlc(ax, with_raw_quotes=False)
subset = slice(-120*3,None) # '2017-07' '2017'
subset = None
plots = pl.Plotter(stk.context, stk, subset) #plot stk data
# plots.plot_candle_only( 'lday')
plots.plot_candle_vol('lday')
#plots.plot_candle_vol('lday', savefig=True)
if align_to=='gg':
return beta, df
else:
return beta2, df2
结果图
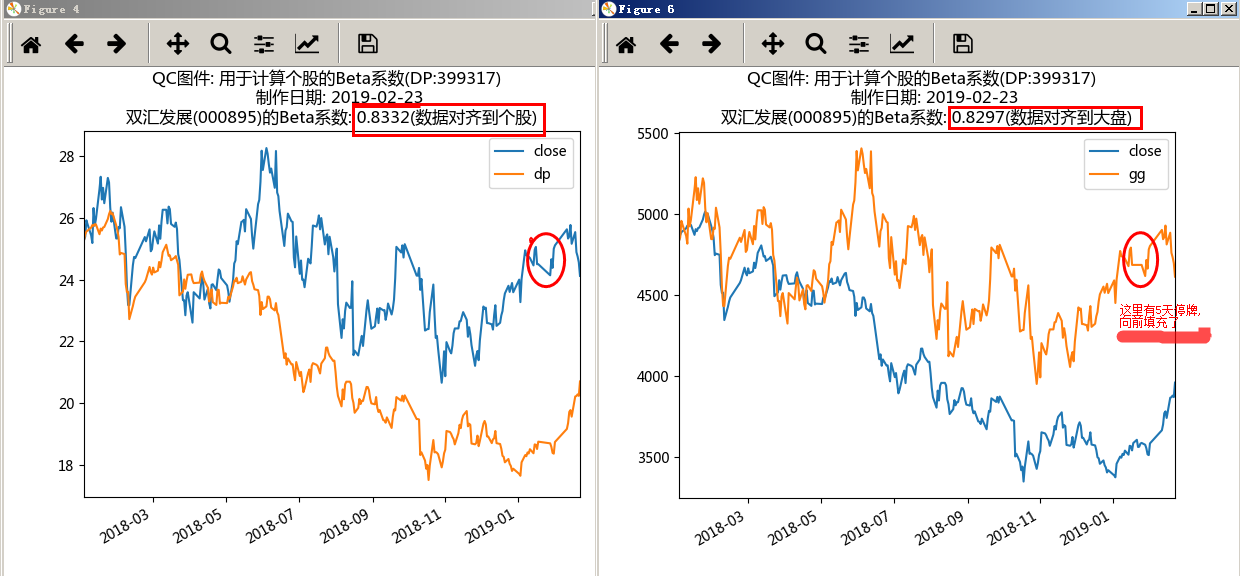
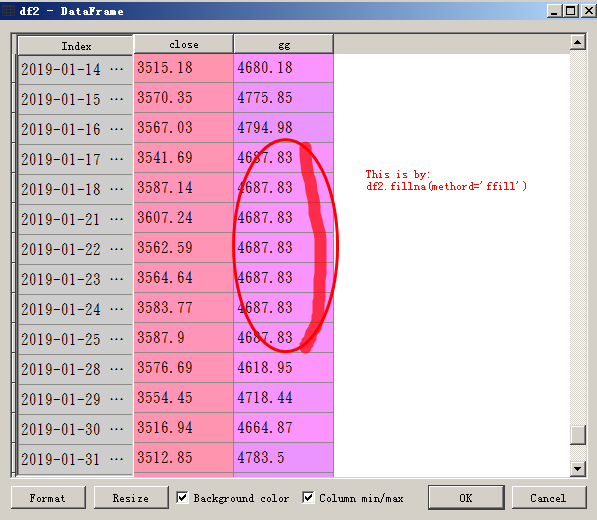
结论
用276天大盘交易日(同期个股是271个交易日)的数据, 采用两种方法, 得到的beta值为:
0.833 vs 0.830
非常接近.
小于1的beta, 揭示了该股在大盘下跌阶段的优异表现.
股票池的beta
代码
def study_block_beta(subset=(8,18,1),show=False):
'''
>>> beta, res = study_block_beta()
>>> beta, res = study_block_beta(show=True)
'''
syms_, syms = read_zxg(subset)
betas, names, codes=[],[],[]
for enum, sym in enumerate(syms):
stk=load_data(sym)
sname = stk.context.name
code = stk.context.code
names.append(sname)
codes.append(code)
pw=sname_print_width(sname)
sdt = str(stk.sdt)[:10]
edt = str(stk.edt)[:10]
prompt = 'loaded data: {:<{pw}} {} {} {}'.format(sname,
code,
sdt, edt,
pw=pw)
print(prompt)
beta=ttr.estimateBeta(stk.ohlc.close, stk.aindex.close)
betas.append(beta)
if show:
#make plot
close = stk.ohlc.close
close = close/close[0] * 10.0
#if not isinstance(fig, plt.Figure):
if enum==0:
fig=plt.figure(); type(fig)
aindex = stk.aindex.close/stk.aindex.close[0] * 10.
ax = aindex.plot(label='国证A指', lw=4, logy=True, ) #use_index=)
close.plot(axes=ax, label=sname, logy=True,)
else:
if enum< len(syms) - 1:
close.plot(axes=ax, label=sname,logy=True,)
else:
close.plot(axes=ax, label=sname,logy=True, title='池子里的收盘线')
ax.legend()
resS = '{} {:8} {:6} {:6} \n'.format('Num','name', 'code', 'Beta')
resS += '-' * 33 + '\n'
for i in range(len(names)):
pw=sname_print_width(names[i])
resS += '{:3d} {:{pw}} {} {:.3f} \n'.format(i, names[i], codes[i], betas[i], pw=pw)
print( resS)
return betas, resS
结果:
Num name code Beta
0 深圳燃气 601139 0.732
1 分众传媒 002027 1.392
2 海康威视 002415 1.378
3 双汇发展 000895 0.839
4 柳 工 000528 1.336
5 上海银行 601229 0.561
6 华兰生物 002007 0.880
7 兖州煤业 600188 1.251
8 云铝股份 000807 1.586
9 神火股份 000933 1.627
300个交易日: 2017-11-28 -- 2019-02-22 时间段的数据:
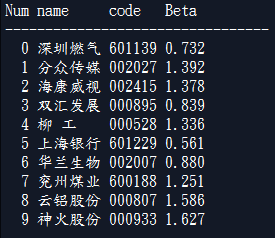
520个交易日: 2017-01-03 -- 2019-02-22 时间段的数据:

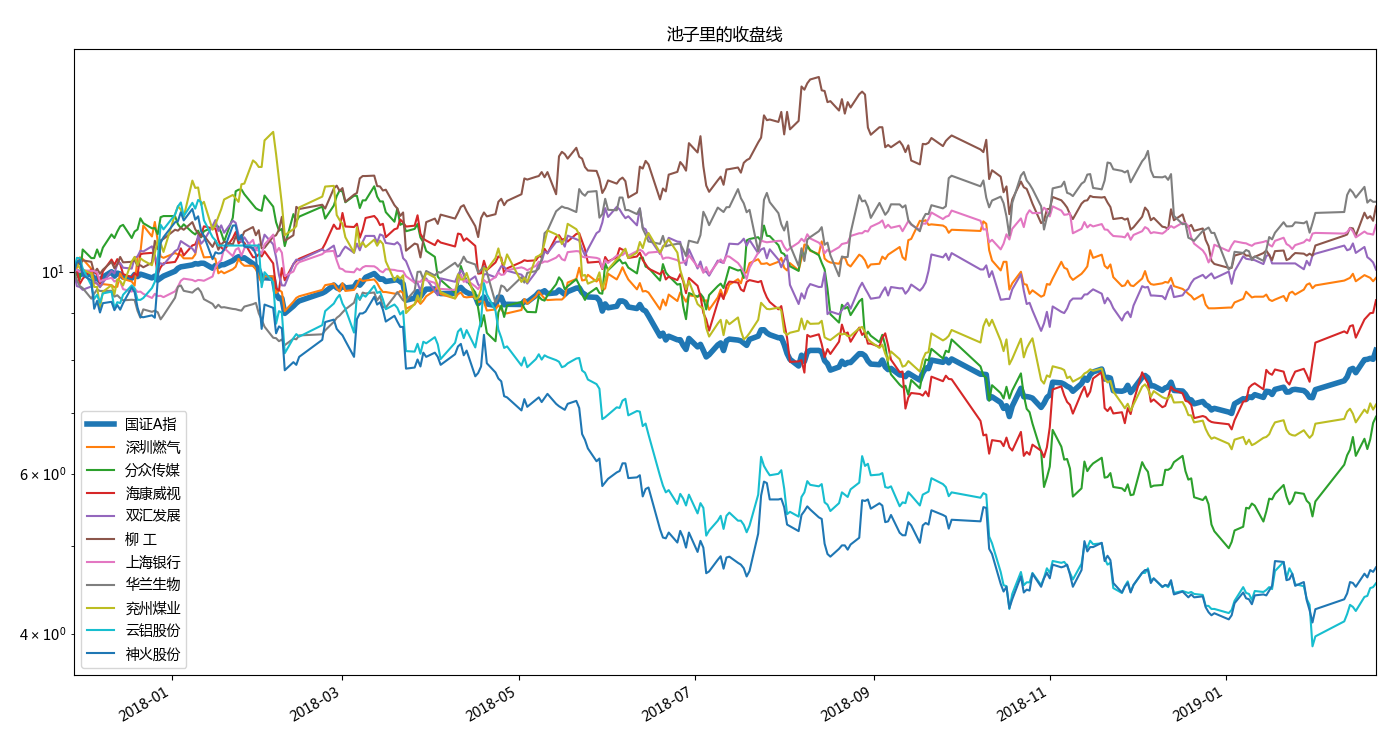

个股和股票池的beta系数的估算的更多相关文章
- 检验两个随机序列的beta系数
检验两个随机序列的beta系数 代码 def test_beta(loops=10): ''' 检验两个随机序列的beta系数 :loops: int, 循环次数, 每次循环会产生两个随机序列, 然后 ...
- 缠中说禅股票交易系统图解 z
缠中说禅股票交易系统图解 2010-03-23 10:51 (王纯阳)缠论祖师的经典语录 1. 就在买点买,卖点卖:当然,买点并不一定是一个点,一个价位,级别越大的,可以容忍的区间越大. 2. 你要经 ...
- 如何使用Pythonapi函数写股票策略
如何使用Python api 函数写股票策略 写策略需要了解的语法包括两方面,一方面是语言本身的语法(包括相关库),另一方面是量化平台提供的api.量化平台提供的api帮助文件里都有了,本文主要介绍写 ...
- python+Sqlite+Dataframe打造金融股票数据结构
5. 本地数据库 很简单的用本地Sqlite查找股票数据. DataSource类,返回的是Dataframe物件.这个Dataframe物件,在之后的业务,如计算股票指标,还需要特别处理. impo ...
- Python之关于量化投资实现代码--根据策略提出的代码--还未完善
# 根据缺口的模式选股买股票 ''' -------------------------------------------- 1.总体回测前要做的事情 initialize(context) 1.1 ...
- <股市高手和你想的不一样>读书笔记
书在这里 在股市中挖掘真正有成长潜力的好企业,是成功投资者的关键 股票被低估的时候,才值得买 我们买股票,就是买这家公司的未来 公司的成长性要重点看两个方面,一个方面要看该公司近三年的成长趋势,另外一 ...
- 【pyhon】理想论坛爬虫1.05版,将读取和写DB分离成两个文件
下午再接再厉仿照Nodejs版的理想帖子爬虫把Python版的也改造了下,但美中不足的是完成任务的线程数量似乎停滞在100个左右,让人郁闷.原因还待查. 先把代码贴出来吧,也算个阶段性成果. 爬虫代码 ...
- 【Nodejs】理想论坛帖子爬虫1.01
用Nodejs把Python实现过的理想论坛爬虫又实现了一遍,但是怎么判断所有回调函数都结束没有好办法,目前的spiderCount==spiderFinished判断法在多页情况下还是会提前中止. ...
- day33 Python与金融量化分析(三)
第三部分 实现简单的量化框架 框架内容: 开始时间.结束时间.现金.持仓数据 获取历史数据 交易函数 计算并绘制收益曲线 回测主体框架 计算各项指标 用户待写代码:初始化.每日处理函数 第四部分 在线 ...
随机推荐
- DOM中表格的操作方法总结
DOM中表格的操作方法总结 <table/>元素的方法如下: caption:指向<caption/>元素(如果存在): tBodies:<tbody/>元素的集合 ...
- SAP顾问岗位要求
岗位职责: 1.负责SAP系统各模块日常运维工作,解决用户在系统操作过程中遇到的问题: 2.评估用户需求(新需求.功能优化)的可实现性,完成SAP系统及相关系统的配置调整及功能实现: 3.负责CRM等 ...
- 微信小程序开发UI组件
第一 view和input和button组件 1.UI组件的通用属性 (1)id 唯一标识 (2)class 设置组件的样式类 (3)style 设置组件的内联样式 (4)hidden ...
- 【gridview增删改查】数据库查询后lodop打印
ASP.NET中使用gridview可以很容易的把需要的数据动态显示在前台,还可以在表格里加入列进行增删改查,每次点击的时候重新加载数据,gridview也提供了分页等功能,还有一些模版让显示在前台的 ...
- 与spring整合就是为了不用自己创建bean 让spring帮助我们创建bean
与spring整合就是为了不用自己创建bean 让spring帮助我们创建bean
- flask再学习-思考之怎么从数据库中查询数据在页面展示!
看别人视频觉得很简单,要自己做蒙蔽了!这样子.NO! 1. 流程: 首先要有和数据库连接的驱动!一般有PYMySQL mysqlclient 等 使用扩展Flask-SQLAlchemy 获得orm对 ...
- docker--Dockerfile--java
# AlpineLinux with a glibc-2.26-r0 and Oracle Java 7FROM alpine:3.6 MAINTAINER Anastas Dancha <an ...
- 【BZOJ3202】项链(莫比乌斯反演,Burnside引理)
[BZOJ3202]项链(莫比乌斯反演,Burnside引理) 题面 BZOJ 洛谷 题解 首先读完题目,很明显的感觉就是,分成了两个部分计算. 首先计算本质不同的珠子个数,再计算本质不同的项链个数. ...
- SharePoint “File not found” 错误
Troubleshooting the SharePoint "File not found" Error Have you ever come across a "Fi ...
- cf827D Best Edge Weight (kruskal+倍增lca+并查集)
先用kruskal处理出一个最小生成树 对于非树边,倍增找出两端点间的最大边权-1就是答案 对于树边,如果它能被替代,就要有一条非树边,两端点在树上的路径覆盖了这条树边,而且边权不大于这条树边 这里可 ...
