运维相关 docker
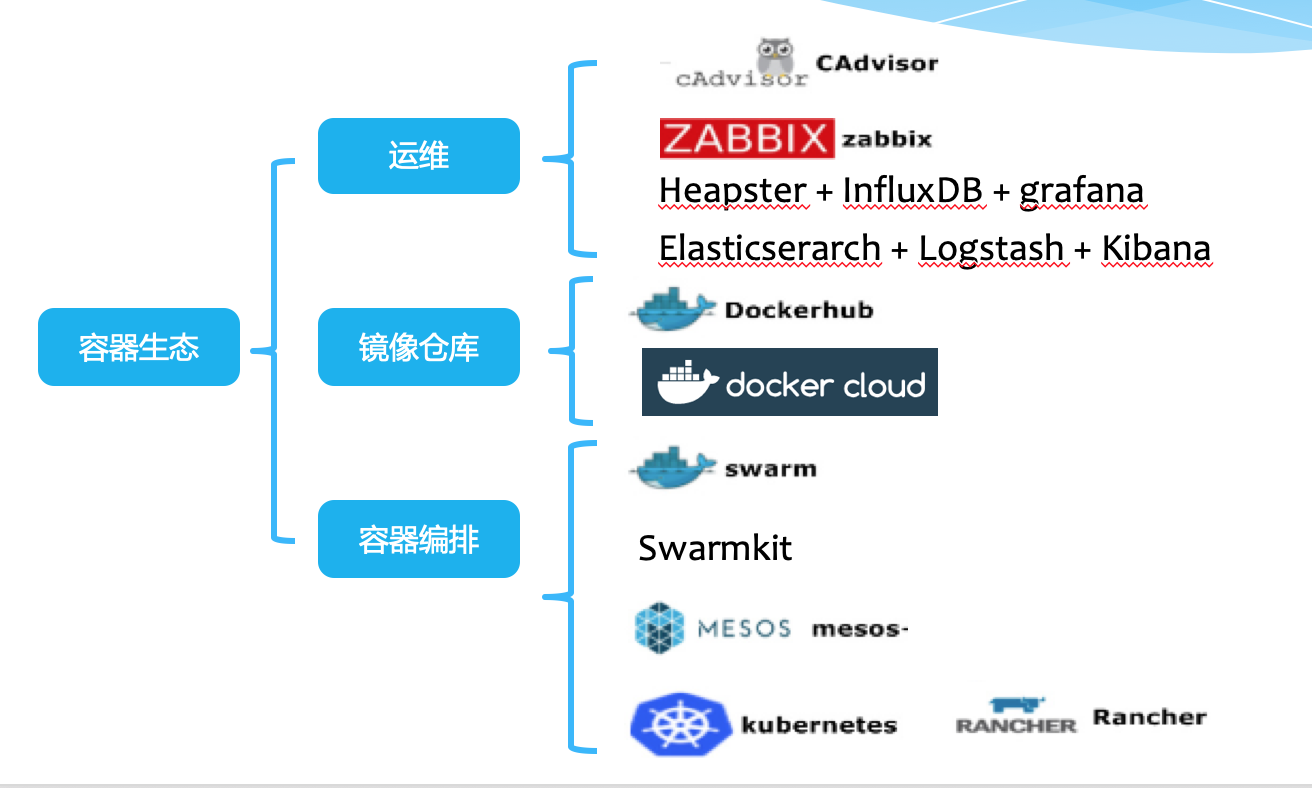
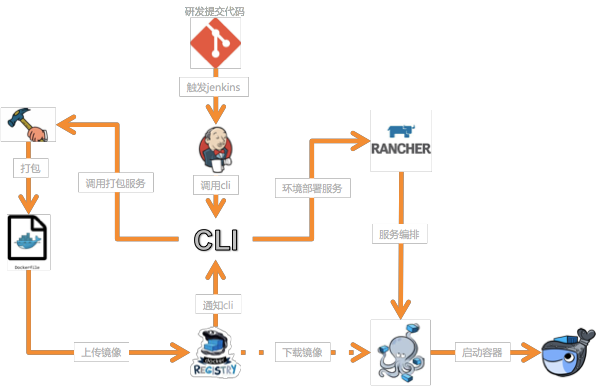
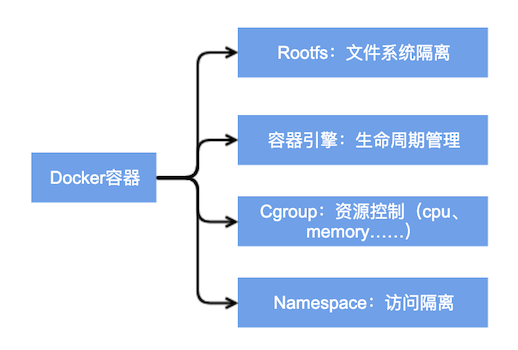
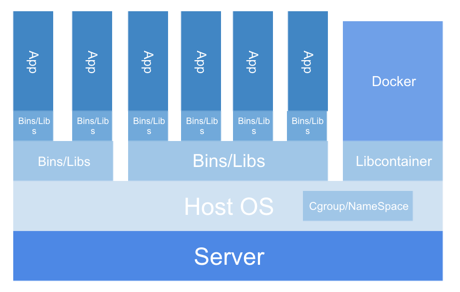
运维相关 docker的更多相关文章
- 新IT运维时代 | Docker运维之最佳实践-下篇
上篇针对操作系统.主机配置.容器镜像.容器运行时四大方面分享一些Docker的运维经验,本篇将着重在Docker Daemon参数和权限两个方面进一步分享.(阅读上篇请点击右侧:新IT运维时代 | D ...
- Open edX 学习、开发、运维相关链接整理
原文地址:http://edustack.org/ 所需知识: Linux Git Python (Django Mako coffeescript sass) (MongoDB Mysql) Ans ...
- redis运维相关(基本数据库命令)【十四】
-----------------------------运维相关------------------------- redis持久化,两种方式1.rdb快照方式2.aof日志方式 --------- ...
- Linux系统运维相关的面试题 (问答题)
这里给大家整理了一些Linux系统运维相关的面试题,有些问题没有标准答案,希望要去参加Linux运维面试的朋友,可以先思考下这些问题. 一.Linux操作系统知识 1.常见的Linux发行版本都有 ...
- 新IT运维时代 | Docker运维之最佳实践-上篇
容器技术的发展可以分为两个阶段,第一个阶段聚焦在IaaS层,仅仅把容器当做更轻量级虚拟机来使用,解决了应用运行时进程级资源隔离的问题:随着Docker的出现,容器虚拟化才有了统一的平台,由此容器技术发 ...
- Linux运维相关目录
- 转载---linux运维相关
前段时间,我在准备面试的时搜到的一套Linux运维工程师面试题,感觉比较全面,一直保存在草稿,刚在整理后台时翻了出来,干脆就发出来好了,以备不时之需. 1.linux如何挂在windows下的共享目录 ...
- Linux网络运维相关
删除特殊的用户和用户组 userdel games group games 关闭不需要的服务 chkconfig chkconfig --level 345 bluetooth off 删减系 ...
- redis运维相关
一.redis都有哪些数据类型?分别在哪些场景下使用比较合适?二.redis双写不一致三.雪崩和穿透四.redis的过期策略,LRU五.redis是如何实现高性能高并发六.如何保证Redis的高并发和 ...
随机推荐
- 【Python】【异步IO】
# [[异步IO]] # [协程] '''协程,又称微线程,纤程.英文名Coroutine. 协程的概念很早就提出来了,但直到最近几年才在某些语言(如Lua)中得到广泛应用. 子程序,或者称为函数,在 ...
- Java中JSONObject相关操作
maven项目pom配置: <dependency> <groupId>net.sf.json-lib</groupId> <artifactId>js ...
- javaee开发模式
model1模式:技术组成:jsp+javaBeanmodel1的弊端:随着业务复杂性 导致jsp页面比较混乱model2模式:技术组成:jsp+servlet+javaBeanmodel2的优点:开 ...
- List<String> list=new ArrayList<String>(20);为什么要声明为List 而不是ArrayList<String>?
如何理解:List<String> list=new ArrayList<String>();为甚麼要声明为List 而不是ArrayList<String>? 在 ...
- Spark强大的函数扩展功能
在数据分析领域中,没有人能预见所有的数据运算,以至于将它们都内置好,一切准备完好,用户只需要考虑用,万事大吉.扩展性是一个平台的生存之本,一个封闭的平台如何能够拥抱变化?在对数据进行分析时,无论是算法 ...
- ArcFace 2.0 Demo [C++]
环境: win10(10.0.16299.0)+ VS2017 sdk版本:ArcFace v2.0 OPENCV3.43版本 x64平台Debug.Release配置都已通过编译 下载地址:http ...
- DRF中的APIView、GenericAPIView、ViewSet
1.APIView(rest_framework.views import APIView),是REST framework提供的所有视图的基类,继承自Django的View. 传入到视图方法中的是R ...
- Codeforces 985 D - Sand Fortress
D - Sand Fortress 思路: 二分 有以下两种构造, 分别二分取个最小. 代码: #include<bits/stdc++.h> using namespace std; # ...
- Python全栈开发-Day8-Socket网络编程
本节内容 断言 Socket构建框架 ftp构建框架 Socket粘包 Socket介绍 Socket参数介绍 基本Socket实例 通过Socket实现简单SSH SocketServer 支持多用 ...
- HTML第一章总结
第一章总结 HTML那些事儿:Web Sever, Web Browser,HTML files 如果你要做网页,那你写了HTML文档就要上传到 Web Server 上 在客户使用 Web Brow ...
