LeetCode - 198 简单动态规划 打家劫舍

你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组，计算你在不触动警报装置的情况下，能够偷窃到的最高金额。

示例 1:

输入: [1,2,3,1]
输出: 4
解释: 偷窃 1 号房屋 (金额 = 1) ，然后偷窃 3 号房屋 (金额 = 3)。
     偷窃到的最高金额 = 1 + 3 = 4 。

示例 2:

输入: [2,7,9,3,1]
输出: 12
解释: 偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9)，接着偷窃 5 号房屋 (金额 = 1)。
     偷窃到的最高金额 = 2 + 9 + 1 = 12 。

我的第一版代码，程序虽然编译通过了，但是运行时间超时

class Solution {
   public static int solve(int index,int []nums)
     {
         //首先计算边界情况
         if(index<0)
             return 0;
         //然后对于当前索引的房屋 有两种情况，一种是抢劫当前房屋，另一种是不抢劫当前房屋
         //能产生最大的抢劫利润的情况有两种一种是
         //1.当前房子+当前房子-2
         //2.不抢当前房子  + 当前房子的前一间
         int max = Math.max(nums[index]+solve(index-2, nums),solve(index-1,nums));
         return max;
     }
     public int rob(int[] nums) {
            return solve(nums.length-1, nums);
     }
}

然后就想起来之前做过的一个  跳n阶台阶的一个问题，可以使用备忘录 的方法 ，也就是使用一个map来存储递归遍历出来的结果

然后第二版代码如下:

package com.zuoyan.leetcode_198;

import java.util.HashMap;
import java.util.Map;

public class Solution {

     public static int solve(int index,int []nums,Map<Integer,Integer> map)
     {
         //首先计算边界情况
         if(index<0)
             return 0;
         if(map.containsKey(index))
         {
             return map.get(index);
         }
         else{
            //然后对于当前索引的房屋 有两种情况，一种是抢劫当前房屋，另一种是不抢劫当前房屋
             //能产生最大的抢劫利润的情况有两种一种是
             //1.当前房子+当前房子-2
             //2.不抢当前房子  + 当前房子的前一间
             int max = Math.max(nums[index]+solve(index-2, nums,map),solve(index-1,nums,map));
             map.put(index, max);
             return max;
         }

     }
     public int rob(int[] nums) {
             Map<Integer, Integer> map = new HashMap<>();
            return solve(nums.length-1, nums,map);
     }

     public static void main(String[] args) {
        Solution solution = new Solution();
        int [] nums = {1,2,3,1};
        int result = solution.rob(nums);
        System.out.println(result);
    }

}

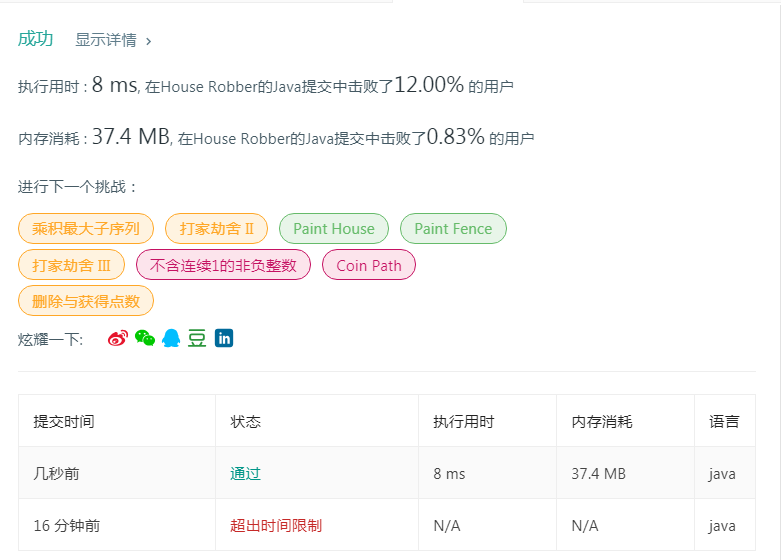
运行结果如下：

显然根据  执行时间击败的用户 和 内存消耗击败的用户可以看出来，我的这个执行效率太低了，就是一种暴力解法，肯定有更好的优化方法。