次短路——Dijkstra

传送门

　　　　　　——在LYC大佬的帮助下过了这道题

思路：

　　LYC大佬的博客里已经讲得很清晰了，我只是提一下要点。

　　求次短路，主要考虑两个方面：

　　①在不重复走一条路的前提下，把最短路的其中一段替换为另一段。

　　②找出最短路中的最短的一条边，重复走两次。（走过来又走回去）

　　分别求出这两方面所能算出的次短路的值，取小的那一条就是答案。

补充：

　　①读入的边要开结构体存起来，后面枚举求次短路要使用。

　　②所谓枚举，就是找出从开始一条一条的读出边的两端点、权值。确定其是否在最短路上（即它的 左端点到源点的最短路+右端点到源点的最短路+自身的边权 是否等于最短路长度。（注意细节：要判断这条边的两端点到源点的最短路是否有重合部分，如下图。）

　　

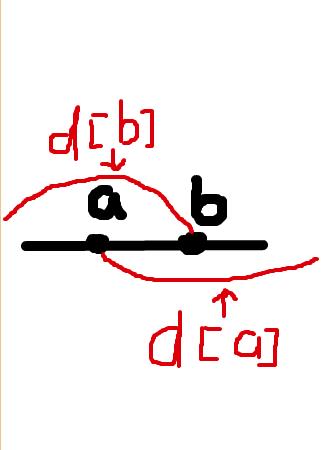
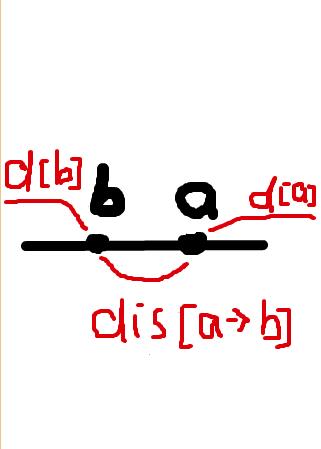
　　设d[ a ]为 a 到源点的最短路，d[ b ]为 b 到源点的最短路，很显然，两条最短路有重合的地方，就需要将 a 点与 b 点交换位置，使得两条最短路没有重合，才能将 a->b 的权值加入。

代码实现：

        if(d1[x]+d2[y]>d1[y]+d2[x]) swap(x,y);

效果如下：

　　

完整代码：

#include<cstdio>
#include<cmath>
#include<cstdlib>
#include<cstring>
#include<string>
#include<iostream>
#include<algorithm>
#include<queue>
#include<stack>
#include<deque>
#include<set>
#include<map>
#include<vector>
#include<fstream>
using namespace std;
#define maxn 1000007
struct edge
{
    int x,y,w;
}dd[maxn];
struct hh
{
    int nex,to,dis;
}t[maxn];
priority_queue<pair<int,int>,vector<pair<int,int> >,greater<pair<int,int> > >q1;
priority_queue<pair<int,int>,vector<pair<int,int> >,greater<pair<int,int> > >q2;//正反两次最短路，两个小根堆
int n,m,cnt=,ans,mi;
int vis[maxn],d1[maxn],d2[maxn],head[maxn];
inline int read()
{
    char kr=;
    char ls;
    for(;ls>''||ls<'';kr=ls,ls=getchar());
    int xs=;
    for(;ls>=''&&ls<='';ls=getchar())
    {
        xs=xs*+ls-;
    }
    if(kr=='-') xs=-xs;
    return xs;
}
inline void add(int nex,int to,int w)
{
    t[++cnt].nex=head[nex];
    t[cnt].to=to;
    t[cnt].dis=w;
    head[nex]=cnt;
}
inline void dijkstra_first(int ww)
{
    memset(d1,0x3f3f3f3f,sizeof(d1));
    memset(vis,,sizeof(vis));
    q1.push(make_pair(,ww));
    d1[ww]=;
    while(!q1.empty())
    {
        int u=q1.top().second;
        q1.pop();
        if(vis[u]) continue;
        vis[u]=;
        for(int v=head[u];v;v=t[v].nex)
        {
            if(d1[t[v].to]>d1[u]+t[v].dis&&!vis[t[v].to])
            {
                d1[t[v].to]=d1[u]+t[v].dis;
                q1.push(make_pair(d1[t[v].to],t[v].to));
            }
        }
    }
}
inline void dijkstra_second(int ww)
{
    memset(d2,0x3f3f3f3f,sizeof(d2));
    memset(vis,,sizeof(vis));
    q2.push(make_pair(,ww));
    d2[ww]=;
    while(!q2.empty())
    {
        int u=q2.top().second;
        q2.pop();
        if(vis[u]) continue;
        vis[u]=;
        for(int v=head[u];v;v=t[v].nex)
        {
            if(d2[t[v].to]>d2[u]+t[v].dis&&!vis[t[v].to])
            {
                d2[t[v].to]=d2[u]+t[v].dis;
                q2.push(make_pair(d2[t[v].to],t[v].to));
            }
        }
    }
}//两次Dijkstra求正反最短路
int main()
{
    n=read();m=read();
    ans=;
    mi=;
    for(int i=;i<=m;++i)
    {
        dd[i].x=read();dd[i].y=read();dd[i].w=read();
        add(dd[i].x,dd[i].y,dd[i].w);
        add(dd[i].y,dd[i].x,dd[i].w);
    }
    dijkstra_first();
    dijkstra_second(n);
    int minn=d1[n];
    for(int i=;i<=m;i++)
    {
        int x=dd[i].x,y=dd[i].y;
        if(d1[x]+d2[y]>d1[y]+d2[x]) swap(x,y);
        int s=d1[x]+d2[y];
        if(s+dd[i].w==minn) continue;
        ans=min(ans,s+dd[i].w);
    }//第一点：不重走边
    for(int i=;i<=m;i++)
    {
        int x=dd[i].x,y=dd[i].y;
        if(d1[x]+d2[y]>d1[y]+d2[x]) swap(x,y);
        if(d1[x]+d2[y]+dd[i].w!=minn) continue;
        mi=min(mi,dd[i].w);//找出最短路中最短的边
    }//第二点：重走边
    ans=min(ans,minn+mi*);//取较小值
    printf("%d\n",ans);
return ;
}

其实两遍的Dijkstra函数可以简化为一遍，多打一遍练练模板。