python记录day_20 多继承

多继承

继承： x是一种y的时候.可以使用继承关系。是"is a"的关系

在python中，支持多继承，一个类可以拥有多个父类。但是多继承中, 存在着这样一个问题，当两个父类中出现了重名方法的时候该怎么办呢? 这时就涉及到如何查找父类方法的问题。即MRO(method resolution order) 问题。在python中这是个很复杂的问题，因为在不同的 python版本中使用的是不同的算法来完成MRO的。

经典类计算MRO用的是深度优先的遍历算法,而新式类的MRO用的是c3算法

##对于经典类和新式类的区分（已经成为过去时了）：

在python2中

没有显式声明继承object类的类及其子类，被称为经典类

有显式声明继承object类的类及其子类，被称为新式类，新式类是在python2.2之后才出现的，在此之前都是用的经典类

python3中默认都继承了object类，所以python3中都是新式类。

#经典类的MRO

深度优先：从左子树开始，右子树结束，一条道走到黑

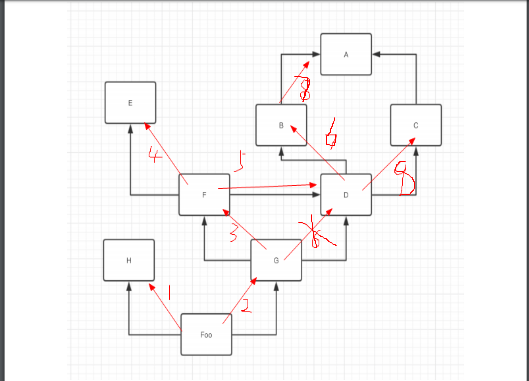
遍历结果： Foo-> H -> G -> F -> E -> D -> B -> A -> C

#新式类的MRO

新式类的MRO是采用的C3算法来完成的，C3的核心是merge

先拆分后合并，合并用merge

merge原则：拿每一项的头和后一项的身体比较，如果出现了，就跳过，从后一项的头继续去比较，如果不出现就拿出这个元素，并删除这个和其他列表中的元素，merge一次后继续从头开始。

 class D(O):
     pass
 class F(O):
     pass
 class C(D,F):
     pass

 # c的mro
 L[C] = C + merge(DO,FO,DF)    #D 和后边其他项的身体都不同，D出来，删除D
      = C + D + merge(O,FO,F)      #O和第二项的身体相同，O跳过，F和后边其他项的身体都不同，F出来，删除F
      = C + D + F + merge(O,O)
      = C D F O

 class A:
     pass
 class B(A):
     pass
 class C(A):
     pass
 class D(B, C):
     pass
 class E(C, A):
     pass
 class F(D, E):
     pass
 class M(F, E):
     pass
 class N:
     pass
 class P(M,N):
     pass
 class G(P):
     pass
 class O:
     pass
 class X(O):
     pass
 class H(G, X, F):
     pass

 '''
 拆分：(注意拆分时在最后面加上所有的子类名)
 L(H) = H + L(G) + L(X) + L(F) + GXF    # 合并： H + GPMFDBECAN + X + FDBECA + GXF =HGPMXFDBECAN

 L(G) = G + L(P)  + P          #   G + PMFDBECAN + P = GPMFDBECAN
 L(X) = X + L(O) + O           #   X + O + O =XO
 L(F) = F + L(D) + L(E) + DE   #   F + DBCA + ECA + DE = FDBECA

 L(P) = P + L(M) + L(N) + MN   #     P + MFDBECA + N +MN = PMFDBECAN
 L(D) = D + L(B) + L(C) + BC   #    合并： D + BA +CA + BC = DBCA
 L(E) = E + L(C) + L(A) + CA   #   合并： E + CA + A + CA = ECA

 L(M) = M + L(F) + L(E) + FE   #  合并： M + FDBECA + ECA + FE = MFDBECA

 '''

 print(H.__mro__)
 结果：
 (<class '__main__.H'>, <class '__main__.G'>, <class '__main__.P'>, <class '__main__.M'>, <class '__main__.X'>, <class '__main__.F'>, <class '__main__.D'>, <class '__main__.B'>, <class '__main__.E'>, <class '__main__.C'>, <class '__main__.A'>, <class '__main__.N'>, <class '__main__.O'>, <class 'object'>)

超难mro题

##

还有一种计算MRO的方法是通过画图，把继承关系看做一个有向无环图进行遍历也能得到正确结果（遍历规则：找入度为0的节点，有多个时，按从左往右的顺序），相对而言这种方式更便捷，详细见下面文章

关于python中Mro的深度解释

http://python.jobbole.com/85685/

##super()

记住super查找的是MRO列表中的下一个