BP神经网络的直观推导与Java实现

人工神经网络模拟人体对于外界刺激的反应。某种刺激经过人体多层神经细胞传递后，可以触发人脑中特定的区域做出反应。人体神经网络的作用就是把某种刺激与大脑中的特定区域关联起来了，这样我们对于不同的刺激就可以调用大脑不同的功能区域进行处理了。

同时，人体神经系统还具有学习，归纳，推理的能力。我们使用计算机模拟了神经网络后，也具有了一定上述能力。

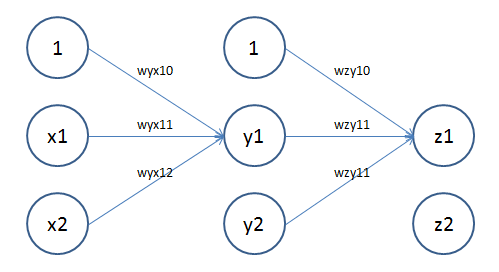
如上图，x层为输入，对应人体接收信号的神经元（比如眼睛，耳朵，手）。y层为隐含层，对应人体的神经网络。z层为输出层，对应人体的大脑。wyx为x层到y层的权重，wzy为y层到x层的权重，对应人体神经细胞间的突触。权重表示了上一层神经细胞对一下层神经细胞的影响大小，一般来说正数表示激发，负数表示抑制，数值越大，影响越大。x0=1是偏移常量。

上述人工神经网络包含两个神经元细胞接收信号（x1,x2），大脑具有两个功能区域对刺激做出反应（z1,z2）。通过学习，我们可以不断调整神经网络中各层权重w，达到某类输入与某类输出的对应关系。

学习过程如下

1、正向传播，计算输出。

y1 = f(wyx10 + wyx11*x1 + wyx12*x2)

y2 = f(wyx20 + wyx21*x1 + wyx22*x2)

z1 = f(wzy10 + wzy11*x1 + wzy12*x2)

z2 = f(wzy20 + wzy21*x1 + wzy22*x2)

这里f(x)为激活函数，神经细胞被激活后，不是简单的把上一层输入信号累加后输出（这样可能导致信号指数增大），而是会适当调整一下再输出，这个调整过程就是f(x)——激活函数。一般来说，f(x)和x正相关，也就是x增大，f(x)也会增大，x减小，f(x)也会减小。我们常常使用f(x)=1/(1+e^-x)作为激活函数。这个函数的好处是f'(x) = f(x) * (1 - f(x))，f'(x)为f(x)的导数。同时，f(x)的函数图像为

2、逆向传播，计算各层误差

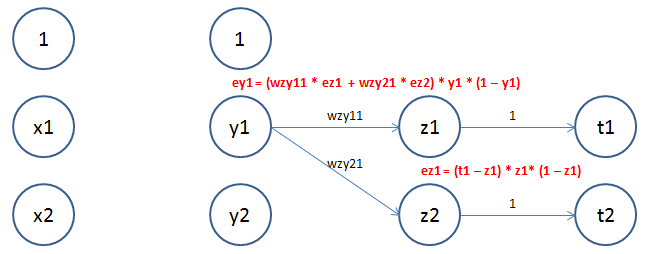
如上图，z1、z2是神经网络输出，t1、t2是输入样本的实际值。ey1为y1神经元输入的误差，ez1为z1神经元输入的误差。

由于真实值为t1，输出值为z1，所以z1的误差显然为t1 - z1。实际上，z1不是z层的直接输入，而是经过激活函数处理后的值。我们记z1的直接输入值为z1'，则z1 = f(z1')。显然z1'的误差

ez1 = (t1 - z1) * f'(z1') = (t1 - z1) * f(z1') * (1 - f(z1'))  = (t1 - z1) * z1 * (1 - z1)

注：直观上来看，f'(x)为f(x)的变化率，所以f(x)的误差ef(x) = ex * f'(x)。

由于y1的误差对z1和z2都有影响，所以，ey1必然包括ez1和ez2，很容易推导出

ey1 = (wzy11 * ez1  + wzy21 * ez2) * y1 * (1 – y1)

3、更新权重

误差都计算出来了，调整权重就是水到渠成的事情。权重调整公式为

wyx10 = wyx10 + rate * ey1 * x0

wyx11 = wyx11 + rate * ey1 * x1

wzy11 = wzy11 + rate * ez1 * y1

公式的含义显而易见，误差为正，则稍微增大输入的权重（增强激发），误差为负，则稍微减小输入的权重（增强抑制），这个是合乎情理的。一般来说，学习速率rate人工设定为一个较小的值。经过多次学习后，最终的输出误差可以控制到一个可接受的范围。

下面是BP神经网络的Java实现。

package com.coshaho.learn.bp;

/**
 *
 * BPCoshaho.java Create on 2018年1月20日 上午11:28:04
 *
 * 类功能说明: BP神经网络
 *
 * Copyright: Copyright(c) 2013
 * Company: COSHAHO
 * @Version 1.0
 * @Author 何科序
 */
public class BPCoshaho
{
    // 第一层输入（原始输入）
    private double[] x;

    // 第二层输入（隐含层结果）
    private double[] y;

    // 第三层输入（预测结果）
    private double[] z;

    // 实际结果
    private double[] t;

    // 第一二层权重
    private double[][] yx;

    // 第二三层权重
    private double[][] zy;

    // 第三层（输出层）误差
    private double[] zError;

    // 第二层（隐含层）误差
    private double[] yError;

    // 学习速率
    private double rate;

    /**
     *
     * 正向计算输出值
     * @author coshaho
     * @param input   上一层输出值
     * @param weight  上一层到本层的权重
     * @param output  本层输出值
     */
    private void calculateNextLevelValue(double[] input, double[][] weight, double[] output)
    {
        output[0] = 1d;
        for(int i = 1; i < output.length; i++)
        {
            double temp = 0d;
            // 下一层节点i的值为上一层每个节点与权重的乘积之和
            for(int j = 0; j < input.length; j++)
            {
                temp = temp + weight[i - 1][j] * input[j];
            }
            // 数据归一化，使用1/(1+e^-x)函数
            temp = 1d / (1d + Math.exp(-temp));
            output[i] = temp;
        }
    }

    /**
     *
     * 逆向计算误差
     * @author coshaho
     * @param nextLevelError   下一层误差。计算输出层误差时，此参数为t
     * @param weight           本层到下一层权重。计算输出层误差时，w为1
     * @param output           本层输出值
     * @param error            本层误差
     */
    private void calculateError(double[] nextLevelError, double [][] weight, double[] output, double[] error)
    {
        // 输出层误差计算:每个输出层误差仅仅和一个目标值关联
        if(null == weight)
        {
            for(int i = 0; i < nextLevelError.length; i++)
            {
                error[i] = (nextLevelError[i] - output[i + 1]) * output[i + 1] * (1 - output[i + 1]);
            }
            return;
        }

        // 隐含层误差计算:每个隐含层误差对输出层所有误差都有影响
        for(int i = 0; i < error.length; i++)
        {
            // 需要把输出层的所有误差分配到隐含层上
            for(int j = 0; j < nextLevelError.length; j++)
            {
                // weight[j][i + 1]表上本层节点i到下一层节点j的权重
                error[i] += nextLevelError[j] * weight[j][i + 1];
            }

            // 误差经过权重累计后，还会使用激活函数进行计算，所以误差还需要乘以一个权重函数的导数
            // f(x) = 1/(1+e^-x)导数为f(x)*(1-f(x))
            error[i] = error[i] * output[i + 1] * (1 - output[i + 1]);
        }
    }

    /**
     *
     * 更新权重
     * @author coshaho
     * @param error    本层误差
     * @param weight   上一层到本层权重
     * @param input    上一层输入
     * @param rate     学习速率
     */
    private void updateWeight(double[] error, double[][] weight, double[] input, double rate)
    {
        // 遍历权重列表调整权重
        for(int i = 0; i < weight.length; i++)
        {
            for(int j = 0; j < weight[i].length; j++)
            {
                // weight[i][j]表示上一层节点j到本层节点i的权重
                weight[i][j] += rate * error[i] * input[j];
            }
        }
    }

    public BPCoshaho(int xSize, int ySize, int zSize, double rate)
    {
        if(xSize < 1 || ySize < 1 || zSize < 1 || 1.0d == rate)
        {
            throw new IllegalArgumentException("Parameter is error.");
        }

        x = new double[xSize + 1];
        y = new double[ySize + 1];
        z = new double[zSize + 1];
        x[0] = 1.0d;
        y[0] = 1.0d;
        z[0] = 1.0d;

        yx = new double[ySize][xSize + 1];
        zy = new double[zSize][ySize + 1];

        zError = new double[zSize];
        yError = new double[ySize];

        this.rate = rate;
    }

    public void train(double[] x, double[] t)
    {
        // 输入训练数据
        setX(x);
        setT(t);

        // 正向传播计算输出值
        calculateNextLevelValue(this.x, yx, y);
        calculateNextLevelValue(y, zy, z);

        // 反向传播计算误差
        calculateError(this.t, null, z, zError);
        calculateError(zError, zy, y, yError);

        // 更新权重
        updateWeight(yError, yx, this.x, rate);
        updateWeight(zError, zy, this.y, rate);
    }

    private void setX(double[] x)
    {
        if(null == x || x.length != this.x.length - 1)
        {
            throw new IllegalArgumentException("Input size is error.");
        }
        System.arraycopy(x, 0, this.x, 1, x.length);
    }

    public double[] predict(double[] x)
    {
        double[] out = new double[z.length - 1];
          setX(x);

        // 正向传播计算输出值
        calculateNextLevelValue(this.x, yx, y);
        calculateNextLevelValue(y, zy, z);

        System.arraycopy(z, 1, out, 0, out.length);
        return out;
    }

    private void setT(double[] t)
    {
        if(null == t || t.length != this.z.length - 1)
        {
            throw new IllegalArgumentException("Target size is error.");
        }
        this.t = t;
    }
}

下面是一个识别正偶数，正奇数，负偶数，负奇数的例子。原理是把整数转换为32位的2进制数输入，然后经过BP神经网络学习，最终达到识别功能。例子中我们仅仅对6000个数字进行训练，但是最后可以识别所有Integer数字，充分说明了BP神经网络的学习，归纳，推理能力。

package com.coshaho.learn.bp;

import java.io.IOException;
import java.util.ArrayList;
import java.util.List;
import java.util.Random;

/**
 *
 * BPTest.java Create on 2018年1月20日 上午11:36:52
 *
 * 类功能说明:   BP测试，识别偶数
 *
 * Copyright: Copyright(c) 2013
 * Company: COSHAHO
 * @Version 1.0
 * @Author 何科序
 */
public class BPTest
{
    public static void main(String[] args) throws IOException
    {
        // 输入层32——对应32 bit integer的每位值。输出层4，对应正奇数，正偶数，负奇数，负偶数。
        BPCoshaho bp = new BPCoshaho(32, 15, 4, 0.05);

        // 生成6000个随机数
        Random random = new Random();
        List<Integer> list = new ArrayList<Integer>();
        for (int i = 0; i != 6000; i++)
        {
            int value = random.nextInt();
            list.add(value);
        }

        // 6000个随机数训练25次
        for (int i = 0; i < 25; i++)
        {
            for (int value : list)
            {
                double[] real = new double[4];
                if (value >= 0)
                {
                    if ((value & 1) == 1)
                    {
                        real[0] = 1;
                    }
                    else
                    {
                        real[1] = 1;
                    }
                }
                else if ((value & 1) == 1)
                {
                    real[2] = 1;
                }
                else
                {
                    real[3] = 1;
                }

                double[] binary = new double[32];
                int index = 31;
                do
                {
                    binary[index--] = (value & 1);
                    // 无符号右移，空位使用0补齐
                    value >>>= 1;
                } while (value != 0);

                bp.train(binary, real);
            }
        }

        System.out.println("Training is done. Please input a integer. ");
        while (true)
        {
            byte[] input = new byte[10];
            System.in.read(input);
            Integer value = Integer.parseInt(new String(input).trim());
            int rawVal = value;
            double[] binary = new double[32];
            int index = 31;
            do
            {
                binary[index--] = (value & 1);
                value >>>= 1;
            }
            while (value != 0);

            // 寻找预测中的最大值
            double[] result = bp.predict(binary);
            double max = -Integer.MIN_VALUE;
            int idx = -1;
            for (int i = 0; i != result.length; i++)
            {
                if (result[i] > max)
                {
                    max = result[i];
                    idx = i;
                }
            }

            switch (idx) {
            case 0:
                System.out.format("%d是一个正奇数\n", rawVal);
                break;
            case 1:
                System.out.format("%d是一个正偶数\n", rawVal);
                break;
            case 2:
                System.out.format("%d是一个负奇数\n", rawVal);
                break;
            case 3:
                System.out.format("%d是一个负偶数\n", rawVal);
                break;
            }
        }
    }
}