【BZOJ3242】【UOJ#126】【NOI2013】快餐店

NOI都是这种难度的题怎么玩嘛QAQ

原题：

小T打算在城市C开设一家外送快餐店。送餐到某一个地点的时间与外卖店到该地点之间最短路径长度是成正比的，小T希望快餐店的地址选在离最远的顾客距离最近的地方。 快餐店的顾客分布在城市C的N 个建筑中，这N 个建筑通过恰好N 条双向道路连接起来，不存在任何两条道路连接了相同的两个建筑。任意两个建筑之间至少存在一条由双向道路连接而成的路径。小T的快餐店可以开设在任一建筑中，也可以开设在任意一条道路的某个位置上（该位置与道路两端的建筑的距离不一定是整数）。 现给定城市C的地图（道路分布及其长度），请找出最佳的快餐店选址，输出其与最远的顾客之间的距离。

N<=10^5，Li<=10^9

恩题解比较好理解但是比较难想到……

首先答案不一定是图上的半径，比如酱：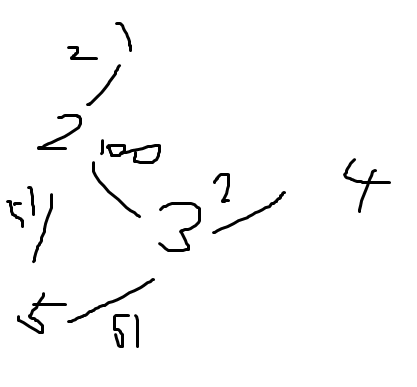

因为有环，所以图上直径的中点到其它所有点距离的最大值可能比半径还要大，这个时候半径就不是最优值

然后显然答案是环上删去某边后树的直径，这个写n^2算法的时候会用到

然后dfs找出环，对环上每个点令其为根求出高度及直径

然后顺着扫一遍，每次记录前面所有环上边的和sum，当前节点子树高度和sum的和的最大值f1，(前面深度最大和次大子树的深度的和)和这两个子树根节点之间的距离的和的最大值f2

然后反过来再搞一遍搞出f3和f4

统计答案即可，注意还有跨过环上第一个点和最后一个点之间的边的情况，这个结合f1和f3就行

最后还要用环上所有点的子树直径的最大值更新ans（不知道为什么QAQ

NOI都是这种难度的题怎么玩嘛QAQ

代码：

 #include<iostream>
 #include<cstdio>
 #include<algorithm>
 #include<cstring>
 #include<cmath>
 using namespace std;
 #define ll long long
 int rd(){int z=,mk=;  char ch=getchar();
     while(ch<''||ch>''){if(ch=='-')mk=-;  ch=getchar();}
     while(ch>=''&&ch<=''){z=(z<<)+(z<<)+ch-'';  ch=getchar();}
     return z*mk;}
 struct edg{int nxt,y,v;}e[];  int lk[],ltp=;
 inline void ist(int x,int y,int z){  e[++ltp]=(edg){lk[x],y,z};  lk[x]=ltp;}
 int n;
 bool vstd[];  int stck[],tp=,fthv[];
 int ccd[],cct=,ccv[];
 ll dp[];
 ll f[],f1[],f2[],f3[],f4[];
 ll mxf=;
 bool gtcc(int x,int y){
     stck[++tp]=x;
     if(vstd[x]){
         fill(vstd,vstd++n,false);
         do vstd[ccd[++cct]=stck[tp]]=true,ccv[cct]=fthv[stck[tp--]];while(stck[tp]!=x);
         return true;}
     vstd[x]=true;
     for(int i=lk[x];i;i=e[i].nxt)if(e[i].y!=y){
         fthv[e[i].y]=e[i].v;
         if(gtcc(e[i].y,x))  return true;}
     --tp;
     return false;}
 void gtdp(int x,int y){
     for(int i=lk[x];i;i=e[i].nxt)if(e[i].y!=y && !vstd[e[i].y]){
         dp[e[i].y]=dp[x]+e[i].v,gtdp(e[i].y,x);
         mxf=max(mxf,f[x]+f[e[i].y]+e[i].v);
         f[x]=max(f[x],f[e[i].y]+e[i].v);}}
 int main(){//freopen("ddd.in","r",stdin);
     int l,r,z;  cin>>n;
     for(int i=;i<=n;++i)  l=rd(),r=rd(),z=rd(),ist(l,r,z),ist(r,l,z);
     if(!gtcc(,))  return ;
     for(int i=;i<=cct;++i)  gtdp(ccd[i],);
     ll bwl=,mx=,ans=,tt=ccv[cct],tmp;  ccv[cct]=;
     for(int i=;i<=cct;++i){
         bwl+=ccv[i-];
         f1[i]=max(f1[i-],bwl+f[ccd[i]]);
         f2[i]=max(f2[i-],mx+bwl+f[ccd[i]]);
         mx=max(mx,f[ccd[i]]-bwl);}
     bwl=mx=;
     for(int i=cct;i>=;--i){
         bwl+=ccv[i];
         f3[i]=max(f3[i+],bwl+f[ccd[i]]);
         f4[i]=max(f4[i+],mx+bwl+f[ccd[i]]);
         mx=max(mx,f[ccd[i]]-bwl);}
     ans=f2[cct];
     for(int i=;i<cct;++i){
         tmp=max(f1[i]+f3[i+]+tt,max(f2[i],f4[i+]));
         ans=min(ans,tmp);}
     ans=max(ans,mxf);
     printf("%.1lf\n",ans*1.0/);
     return ;}