Codeforces 488B - Candy Boxes

B. Candy Boxes

题目链接：http://codeforces.com/problemset/problem/488/B

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

There is an old tradition of keeping 4 boxes of candies in the house in Cyberland. The numbers of candies are special if their arithmetic mean, their median and their range are all equal. By definition, for a set {x1, x2, x3, x4} (x1 ≤ x2 ≤ x3 ≤ x4) arithmetic mean is 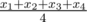, median is  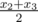and range is x4 - x1. The arithmetic mean and median are not necessary integer. It is well-known that if those three numbers are same, boxes will create a "debugging field" and codes in the field will have no bugs.

For example, 1, 1, 3, 3 is the example of 4 numbers meeting the condition because their mean, median and range are all equal to 2.

Jeff has 4 special boxes of candies. However, something bad has happened! Some of the boxes could have been lost and now there are only n (0 ≤ n ≤ 4) boxes remaining. The i-th remaining box contains ai candies.

Now Jeff wants to know: is there a possible way to find the number of candies of the 4 - n missing boxes, meeting the condition above (the mean, median and range are equal)?

Input

The first line of input contains an only integer n (0 ≤ n ≤ 4).

The next n lines contain integers ai, denoting the number of candies in the i-th box (1 ≤ ai ≤ 500).

Output

In the first output line, print "YES" if a solution exists, or print "NO" if there is no solution.

If a solution exists, you should output 4 - n more lines, each line containing an integer b, denoting the number of candies in a missing box.

All your numbers b must satisfy inequality 1 ≤ b ≤ 106. It is guaranteed that if there exists a positive integer solution, you can always find such b's meeting the condition. If there are multiple answers, you are allowed to print any of them.

Given numbers ai may follow in any order in the input, not necessary in non-decreasing.

ai may have stood at any positions in the original set, not necessary on lowest n first positions.

Examples

input

2
1
1

output

YES
3
3

input

3
1
1
1

output

NO

input

4
1
2
2
3

output

YES
题目大意：输入一个整数n,代表n个糖果盒子，接下来n个数，代表每个糖果盒子中的糖果数；看是否可以添加4-n个糖果盒子，组成4个糖果盒子（糖果盒中的糖果数记为a<=b<=c<=d），

使得（a+b+c+d）/4=(b+c)/2=d-a。如果不可以，输出NO;否则，输出YES以及添加的糖果盒子中的糖果数。

方法及证明：
分类谈论。

由

（a+b+c+d）/4=(b+c)/2=d-a

得①d=3a;②b+c=4a.
将糖果数保存进box[]中，并升序排序。
（1）当n==0，肯定存在，输出YES以及1，1，3，3；
（2）当n==1时，也肯定存在，输出YES以及box[0],box[0]*3,box[0]*3;
（3）当n==2时，如果box[0]和box[1]分别在a和b位置不满足条件，那么他们在任何位置也不满足条件，下面给出证明：
　　由①得d=3*box[0]>0(满足条件)
   由②得c=4*box[0]-box[1]
   如果要不满足条件，那么只能是4*box[0]-box[1]<=0,得box[1]>=4*box[0]
　　Ⅰ当box[0]和box[1]分别在a和c位置时，b=4*box[0]-box[1]<=0,不满足条件；
　　Ⅱ当box[0]和box[1]分别在a和d位置时,box[1]=3*a=3*box[0],因为box[1]>=4*box[0],所以，3*box[0]>=4*box[0]，矛盾；
　　Ⅲ当box[0]和box[1]分别在b和c位置时,a=(box[0]+box[1])/4>=(5/4)*box[0]>box[0]=b，不满足升序条件；
　　Ⅳ当box[0]和box[1]分别在b和d位置时，a=d/3=box[1]/3>=(4/3)*box[0]>box[0]=b,不满足升序条件。
   证毕。
　　所以，只要满足4*box[0]-box[1]>0,就一定存在；否则一定不存在。
（4）当n==3时，根据①②分别讨论box[0]box[1]box[2]在b,c,d或a,c,d(或a,b,d这2种类似)或a,b,c位置的情形，如果你上面的证明看懂了，那么这个对你来说就是小case了。
（5）当n==4时，看满不满足（a+b+c+d）/4=(b+c)/2=d-a。
代码如下：

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
const int N=1e6;
int main()
{
    int n;
    int box[];
    cin>>n;
    int sum=;
    for(int i=;i<n;i++)
    {
        cin>>box[i];
        sum+=box[i];
    }
    sort(box,box+n);
    if(n==)
    {
        float ave=sum/4.0;
        float med=(box[]+box[])/2.0;
        float range=box[]-box[];
        if(ave==med&&med==range)cout<<"YES"<<endl;
        else cout<<"NO"<<endl;
    }
    else if(n==)
    {
        if(box[]%==&&(box[]+box[])%==&&box[]/==(box[]+box[])/)
        {
            cout<<"YES"<<endl;
            cout<<box[]/<<endl;
        }
        else if(box[]==box[]*&&box[]*>box[])
        {
            cout<<"YES"<<endl;
            cout<<box[]*-box[]<<endl;
        }
        else if((box[]+box[])%==&&box[]==(box[]+box[])/)
        {
            cout<<"YES"<<endl;
            cout<<box[]*<<endl;
        }
        else
        cout<<"NO"<<endl;
    }
    else if(n==)
    {
        int c=box[]*-box[];
        int d=box[]*;
        if(c<=)cout<<"NO"<<endl;
        else
        {
            cout<<"YES"<<endl;
            cout<<c<<endl;
            cout<<d<<endl;
        }
    }
    else if(n==)
    {
        cout<<"YES"<<endl;
        cout<<box[]<<endl;
        cout<<box[]*<<endl;
        cout<<box[]*<<endl;
    }
    else if(n==)
    {
        cout<<"YES"<<endl;
        cout<<<<endl;
        cout<<<<endl;
        cout<<<<endl;
        cout<<<<endl;
    }
    return ;
}