网络编程中select模型和poll模型学习(linux)

一、概述

并发的网络编程中不管是阻塞式IO还是非阻塞式IO，都不能很好的解决同时处理多个socket的问题。操作系统提供了复用IO模型：select和poll，帮助我们解决了这个问题。这两个函数都能够允许进程指示内核等待多个事件中的任何一个发生，并只在有一个或多个事件发生或者经历一段指定的时间后才唤醒它。

二、select模型

1、函数定义

2、函数解析

（1）maxfd1参数指定待测试的描述符的个数，它的值是所有待测试描述符中最大者加1，描述符0,1,2,...一直到maxfd1-1均被测试。（windows中该参数没有意义）

（2）fd_set是一个描述符集类型，通常是一个整数数组，数组中每个整数它们二进制形式中的每一位对应一个描述符的状态。详细参考：http://blog.csdn.net/pinhole/article/details/54575204

通过以下四个宏可以管理描述符

select模型中能够管理的描述符数量是有限制的，最多不能超过FD_SETSIZE，这个宏定义定义在<sys/select.h>头文件中。这个值虽然可以通过修改内核修改，但是会影响通信的效率。所以针对这个限制，操作系统提供了poll模型。

readset、writeset和exceptset分别设置我们对读、写和异常检测的描述符。不需要检测的条件可以将对应的描述符集置为空。这三个参数是值-结果参数，调用时，我们指定所关心的描述符的值，函数返回时，结果将指示哪些描述符已就绪(就绪的话描述符集对应二进制位为1)。

（3）timeout可以设置三个值：置为空，表示仅在有一个描述符准备好IO才返回，否则永远等下去；置为指定的秒数和微秒数，在有一个描述符准备好或者超时后，select返回；置为0，则select会检查完描述符后立即返回，相当于轮巡。

（4）返回值

该函数的返回值表示描述符集中满足条件的描述符个数。如果在任何描述符就绪前定时器到时，那么返回0。返回-1表示错误。

3、描述符就绪的条件

（1）满足下列四个条件中的任何一个，一个套接字准备好读

a）该套接字接收缓冲区中的数据字节数大于等于套接字接收缓冲区低水位标记

b）该连接的读半部关闭（也就是接受了FIN的TCP连接）

c）该套接字是一个监听套接字并且已完成的连接数不为0。接下来可以通过accept接收连接客户端套接字

d）有一个套接字错误待处理

（2）满足下列四个条件中的任何一个，一个套接字准备好写

a）该套接字发送缓冲区中的数据字节数大于等于套接字发送缓冲区低水位标记

b）该连接的写半部关闭

c）使用非阻塞式connect的套接字已建立连接，或者connect已经以失败告终

d）有一个套接字错误待处理

（3）如果一个套接字存在带外数据或者仍处于带外标记，那么它有异常条件待处理。

三、poll模型

1、函数定义

2、函数解析

（1）第一个参数是一个pollfd类型的数组，用于指定测试某个给定描述符fd的条件。

fd为要测试的描述符，events为要测试的条件，revents存放函数返回后该描述符的状态。和select函数中间的三个值-结果参数不同，poll将值和结果分开。events和revents由下列值按位或构成。

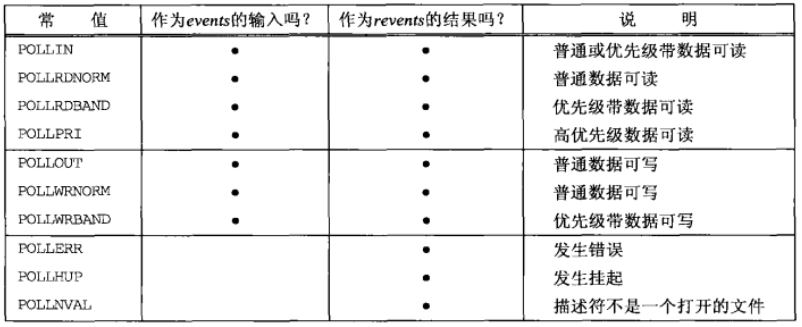
（2）nfds为第一个参数数组的个数。

（3）timeout参数指定poll函数返回前等待多长时间。为INFTIM(-1)表示永远等待，直到描述符满足相应的条件；为0表示立即返回，不阻塞；大于0表示等待指定的毫秒数或者描述符满足相应的条件。

（4）返回值

当发生错误时，poll函数返回-1；若定时器到时之前没有任何描述符满足条件，返回0；否则返回就绪描述符的个数，即revents成员值非0的描述符个数。

（5）如果我们不再关心某个描述符，那么可以把与它对应的pollfd数组的fd成员设置成一个负值。poll函数将忽略这样的pollfd结构的events成员，返回时将它的revents成员的值置为0。

实现代码：http://download.csdn.net/detail/pinhole/9738939