ACA：利用ACA解决TSP优化最佳路径问题——Jason niu

load citys_data.mat  
n = size(citys,1);
D = zeros(n,n);
for i = 1:n
    for j = 1:n
        if i ~= j
            D(i,j) = sqrt(sum((citys(i,:) - citys(j,:)).^2));
        else
            D(i,j) = 1e-4;
        end
    end
end

m = 50;
alpha = 1;
beta = 5;
rho = 0.1;
Q = 1;
Eta = 1./D;
Tau = ones(n,n);
Table = zeros(m,n);
iter = 1;
iter_max = 200;
Route_best = zeros(iter_max,n);
Length_best = zeros(iter_max,1);
Length_ave = zeros(iter_max,1);      

while iter <= iter_max
      start = zeros(m,1);
      for i = 1:m
          temp = randperm(n);
          start(i) = temp(1);
      end
      Table(:,1) = start;
      citys_index = 1:n;
      for i = 1:m
         for j = 2:n
             tabu = Table(i,1:(j - 1));
             allow_index = ~ismember(citys_index,tabu);
             allow = citys_index(allow_index);
             P = allow;

             for k = 1:length(allow)
                 P(k) = Tau(tabu(end),allow(k))^alpha * Eta(tabu(end),allow(k))^beta;
             end
             P = P/sum(P);
             Pc = cumsum(P);
            target_index = find(Pc >= rand);
            target = allow(target_index(1));
            Table(i,j) = target;
         end
      end
      Length = zeros(m,1);
      for i = 1:m
          Route = Table(i,:);
          for j = 1:(n - 1)
              Length(i) = Length(i) + D(Route(j),Route(j + 1));
          end
          Length(i) = Length(i) + D(Route(n),Route(1));
      end
      if iter == 1
          [min_Length,min_index] = min(Length);
          Length_best(iter) = min_Length;
          Length_ave(iter) = mean(Length);
          Route_best(iter,:) = Table(min_index,:);
      else
          [min_Length,min_index] = min(Length);
          Length_best(iter) = min(Length_best(iter - 1),min_Length);
          Length_ave(iter) = mean(Length);
          if Length_best(iter) == min_Length
              Route_best(iter,:) = Table(min_index,:);
          else
              Route_best(iter,:) = Route_best((iter-1),:);
          end
      end

      Delta_Tau = zeros(n,n);
      for i = 1:m
          for j = 1:(n - 1)
              Delta_Tau(Table(i,j),Table(i,j+1)) = Delta_Tau(Table(i,j),Table(i,j+1)) + Q/Length(i);
          end
          Delta_Tau(Table(i,n),Table(i,1)) = Delta_Tau(Table(i,n),Table(i,1)) + Q/Length(i);
      end
      Tau = (1-rho) * Tau + Delta_Tau;
    iter = iter + 1;
    Table = zeros(m,n);
end

[Shortest_Length,index] = min(Length_best);
Shortest_Route = Route_best(index,:);
disp(['最短距离:' num2str(Shortest_Length)]);
disp(['最短路径:' num2str([Shortest_Route Shortest_Route(1)])]);

subplot(1,2,1);
plot([citys(Shortest_Route,1);citys(Shortest_Route(1),1)],...
     [citys(Shortest_Route,2);citys(Shortest_Route(1),2)],'o-');
grid on
for i = 1:size(citys,1)
    text(citys(i,1),citys(i,2),['   ' num2str(i)]);
end
text(citys(Shortest_Route(1),1),citys(Shortest_Route(1),2),'       起点');
text(citys(Shortest_Route(end),1),citys(Shortest_Route(end),2),'       终点');
xlabel('城市位置横坐标')
ylabel('城市位置纵坐标')
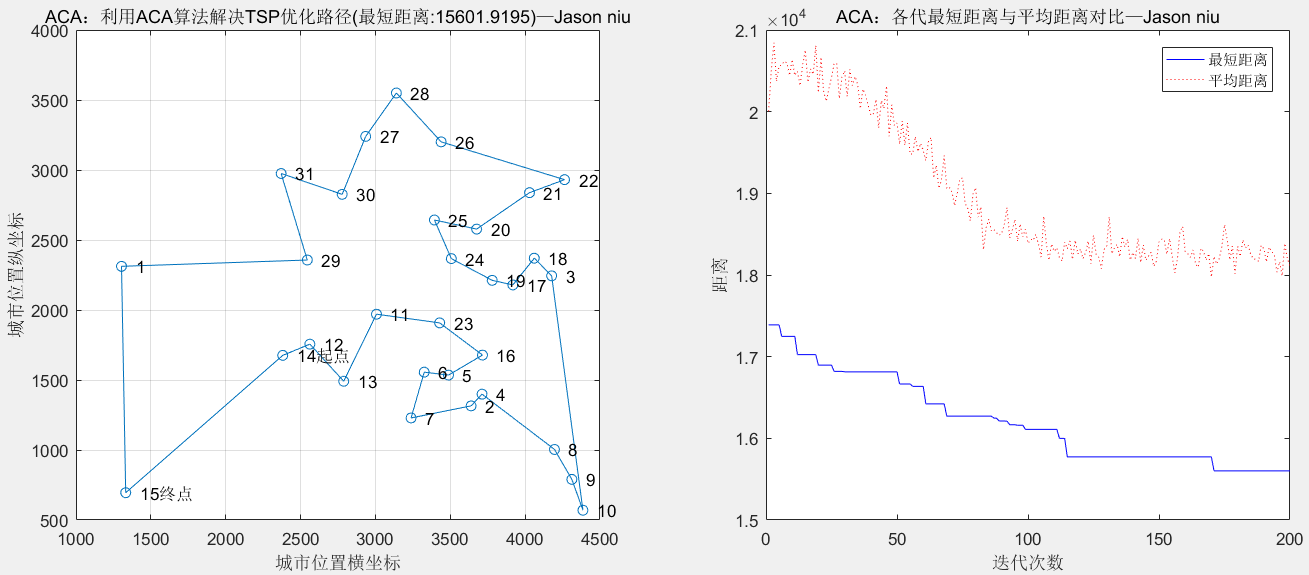
title(['ACA：利用ACA算法解决TSP优化路径(最短距离:' num2str(Shortest_Length) ')—Jason niu'])
subplot(1,2,2);
plot(1:iter_max,Length_best,'b',1:iter_max,Length_ave,'r:')
legend('最短距离','平均距离')
xlabel('迭代次数')
ylabel('距离')
title('ACA：各代最短距离与平均距离对比—Jason niu')