[IOI2007] sails 船帆

显然答案与杆的顺序无关（按每个高度考虑）。

从高到低考虑杆，设此时的状态为\(S\)，\(S[i]\)是高度\(i\)的帆的数目，初始全为\(0\)，当前杆的高度为\(h\)，杆上需要放置的帆的数目为\(k\)，贪心地，假设两个高度的同等宜选，优先选择更高的；帆尽量放置在\(S[i]=0(i\le h)\)的高度上，若还有剩余，设剩下\(t(t\le k)\)个，则放置在除去以选择的高度以外，\(S[i](i\le h)\)前\(t\)小的位置。

整理一下，每次选出\(S[1\cdots h]\)中前\(k\)小的（相同大小选下标较大的）高度放置帆。

{5,3} 0 0 1 1 1  +0
{4,3} 1 1 2 1 1  +1
{4,1} 1 2 2 1 1  +1
{3,2} 2 2 3 1 1  +3
{3,2} 3 3 3 1 1  +4
{2,1} 3 4 3 1 1  +3

但是此时\(S\)似乎不好维护。。考虑将过程倒过来，从低到高考虑杆，（\(S\)一开始为空集，其余定义相同），假设两个高度同等宜选，优先选择更低的，其余大致相同。即每次选出\(S[1\cdots h]\)中前\(k\)小的（相同大小选下标较小的）高度放置帆。

{2,1} 1 0        +0
{3,2} 1 1 1      +0
{3,2} 2 2 1      +2
{4,1} 2 2 1 1    +0
{4,3} 3 2 2 2    +4
{5,3} 3 3 3 2 1  +4

这样用平衡树维护\(S\)（初始大小为0，每次长度变化时补0节点），每次查询全局前\(k\)小然后整体加一即可。（省去了下标范围的约束）。进一步可发现，连下标都不用维护了

---

巧妙的分割线（之前的splay已经弃坑了）

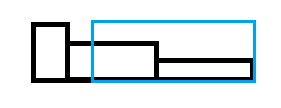
观察各个时态的\(S\)，发现它总是一个单调不增的序列，把某时态的\(S\)中相同且相邻分成一块，如图，蓝色方框表示将选出前\(k\)小的位置，注意被完全覆盖的块的高度可以直接区间+1，而割开的块区间+1的范围是反过来的，显然这样的块最多一块，于是可以上线段树来维护。

答案也不用每步累加，设\(S[i]\)表示最终状态上高度为\(i\)的帆的数目，显然总答案是\(\sum_i\frac{S[i](S[i]-1)}2\)，这与因为从本文第一句照应。

#include <bits/stdc++.h>
#define LL long long
const int N=1e5+10;

namespace sgt {
	struct sgtNode {
		int mx,mn,add;
	} t[N<<2];
#define ls (x<<1)
#define rs (x<<1|1)
	void update(int x) {
		t[x].mx=std::max(t[ls].mx,t[rs].mx);
		t[x].mn=std::min(t[ls].mn,t[rs].mn);
	}
	void pushr(int x,int add) {t[x].mn+=add,t[x].mx+=add,t[x].add+=add;}
	void pushdown(int x) {
		if(t[x].add) pushr(ls,t[x].add),pushr(rs,t[x].add),t[x].add=0;
	}
	LL calc(int x,int l,int r) {
		if(l==r) return 1LL*t[x].mx*(t[x].mx-1)/2;
		int mid=(l+r)>>1; pushdown(x);
		return calc(ls,l,mid)+calc(rs,mid+1,r);
	}
	void build(int x,int l,int r) {
		t[x].mn=+1e9,t[x].mx=-1e9;
		if(l==r) return; int mid=(l+r)>>1;
		build(ls,l,mid); build(rs,mid+1,r);
	}
	void insert(int x,int l,int r,int p) {
		if(l==r) return void(t[x].mx=t[x].mn=0);
		int mid=(l+r)>>1; pushdown(x);
		if(p<=mid) insert(ls,l,mid,p);
		else insert(rs,mid+1,r,p);
		update(x);
	}
	void modify(int x,int l,int r,int L,int R) {
		if(L>R) return;
		if(L<=l&&r<=R) return pushr(x,1);
		int mid=(l+r)>>1; pushdown(x);
		if(L<=mid) modify(ls,l,mid,L,R);
		if(mid<R) modify(rs,mid+1,r,L,R);
		update(x);
	}
	int getVal(int x,int l,int r,int p) {
		if(t[x].mn==t[x].mx) return t[x].mn;
		int mid=(l+r)>>1; pushdown(x);
		if(p<=mid) return getVal(ls,l,mid,p);
		else return getVal(rs,mid+1,r,p);
	}
	int getRangeL(int x,int l,int r,int w) {
		if(l==r) return l;
		int mid=(l+r)>>1; pushdown(x);
		if(t[ls].mn<=w) return getRangeL(ls,l,mid,w);
		else return getRangeL(rs,mid+1,r,w);
	}
	int getRangeR(int x,int l,int r,int w) {
		if(l==r) return l;
		int mid=(l+r)>>1; pushdown(x);
		if(t[rs].mx>=w) return getRangeR(rs,mid+1,r,w);
		else return getRangeR(ls,l,mid,w);
	}
}

int n,m;
std::pair<int,int> a[N];

int main() {
	scanf("%d",&n);
	for(int i=1; i<=n; ++i) {
		scanf("%d%d",&a[i].first,&a[i].second);
		m=std::max(m,a[i].first);
	}
	std::sort(a+1,a+n+1);
	sgt::build(1,1,m);
	for(int i=1,R=0; i<=n; ++i) {
		while(R<a[i].first) sgt::insert(1,1,m,++R);
		int pos=R-a[i].second+1; //被割开的位置
		int val=sgt::getVal(1,1,m,pos);
		int rgl=sgt::getRangeL(1,1,m,val);
		int rgr=sgt::getRangeR(1,1,m,val);

//		std::cout<<val<<' '<<rgl<<' '<<rgr<<std::endl;

		sgt::modify(1,1,m,rgr+1,R);
		sgt::modify(1,1,m,rgl,rgl+a[i].second-(R-rgr)-1);
	}
	printf("%lld\n",sgt::calc(1,1,m));
	return 0;
}