清北学堂Day3
卷积公式(Dirichlet卷积)

这个式子看上去就很变态,那么他是什么意思呢:
就是说
函数f(x)和g(x)对于n的卷积等于n的每一个因子d在f(x)上的值乘上d/n在g(x)上的值的和
例:
设g(n)=φ(n),f(n)=n;
求(f*g)(12)=?;
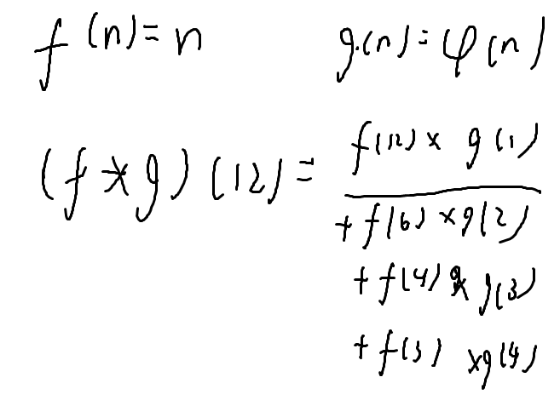
时间复杂度的话,首先要枚举所有的因子o(sqrt(d) ,所以整个的时间复杂度就是o(n*sqrt(n))
有一个非常神奇的筛法
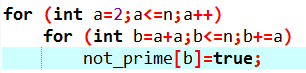
这个筛法其实和埃氏筛是差不多的,换了个写法而已,但是:
我们用这个循环方式的话,就可以改变时间复杂度
有一个很有意思的东西
1 +1/2+1/3 +1/4 + 1/5+ 1/6+1/7+1/8 +...=logN;
ll f[N],g[N],h[N];
void calc(int n)
{
for(int i=;i*i<=n;i++)
{
h[i*j]+=f[i]*g[i];
for(int j=i+;i*j<=n;j++)
h[i*j]+=f[i]*g[j]+f[j]*g[i];
}
}
这样这个筛法的时间复杂度可以变成n(1 +1/2+1/3 +1/4 + 1/5+ 1/6+1/7+1/8 +...)即o (n logN);
数论题目有一个很好的技巧,只要我们把循环的顺序换一下,很多时候时间复杂度就降下来了,而且数论题目很多也都是考的对算法的优化;很多时候公式推出来了,到最后优化写的不行就直接TLE,这是非常悲催的事情
例题:
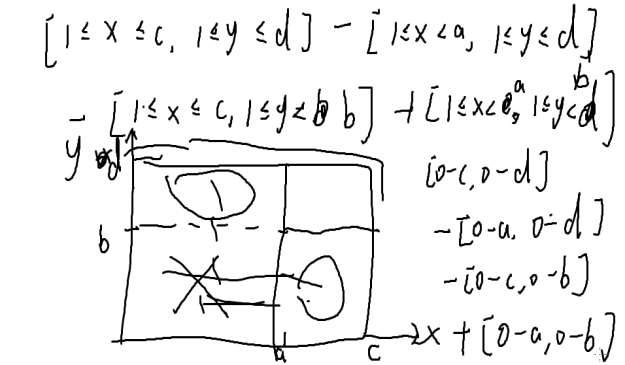
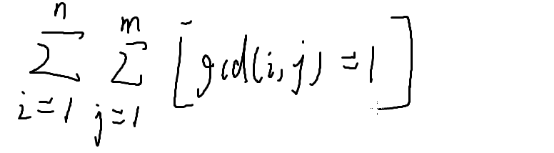
[]表示如果为真返回1,否则返回0;

这样就能换成了对所有因子的莫比乌斯函数求值
再换一下,把d放在前面,就大大优化了
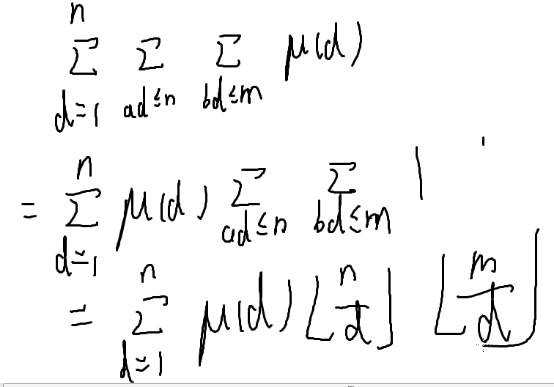
这里[ ]是向下取整,要注意不要和上面的判断真假混淆

这里运用了一个非常重要的思想,也就是分块,其实就是通过下取整的方式来把枚举的数字快速筛掉
其实看一下取整函数的图像就能很好发现
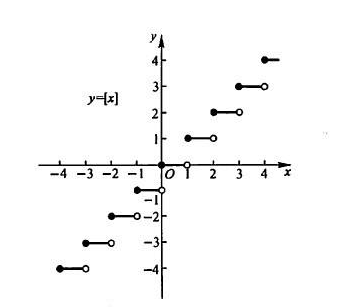
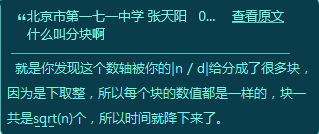
实际上n/[n/d]就是区间的右端点

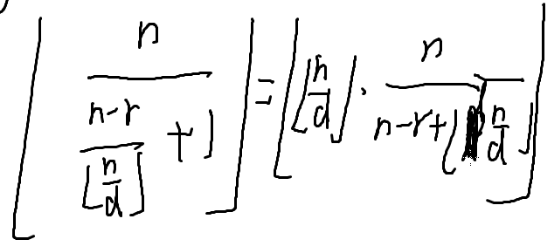
代码实现
xian_xing_shai(); for (int a=;a<=n;a++)
sum_mu[a] = sum_mu[a-] + mu[a]; int solve(int n,int m)
{
int ans=;
//for (int d=1;d<=n;d++)
// ans += mu[d] * (n/d) * (m/d);
for (int d=;d<=n;)
{
int next_d = min(
n/(n/d),
m/(m/d)
);
ans += (sum_mu[next_d] - sum_mu[d-]) * (n/d) * (m/d);
d=next_d+;
}
return ans;
}
组合数


取两册文字不同的书的方案=取日文英文+取日文中文+取英文中文
相同的:取日文日文,取中文中文,取英文英文
随便取两册:上两问加起来

考虑两面旗帜的方法和三盆花的方法,根据乘法原理乘起来即可
ans=P(5,2)*P(20,3)

先考虑对七名男生排序,然后在六个间隔中插入三名女生
ans=P(7,7)*P(6,3)

先看个位数:有0,2,4,6,8五种情况,对于0和8,它的千位数都是有2,3,4,5,6五种情况,对于剩下的三个数,各有2,3,4,5,6中除去它自己四种情况,故千位和个位可能的情况共有:2*5+4*3=22 种 ,然后对百位和十位排序,有P(8,2)种情况
故ans=22*P(8,2)

总的方案数减去选上男A和女B的方案数
ans=C(12,5)-C(10,3)

按余数分类:余数相同和余数不同
余数相同分为:(0,0,0),(1,1,1).(2,2,2);
1~300这些数中,余数相同的各有100个
故每一种可能的方式均为C(100,3)
余数不同时,每一个数都是从不同的余数中选一个,故方式为C(100,1)3
ans=3*C(100,3)+C(100,1)3

由于每种颜色的旗帜是相同的,所以讲相同颜色的旗帜放一起,只能算是一种方式

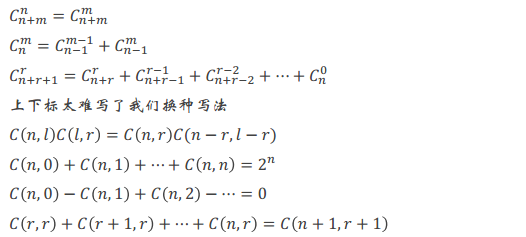

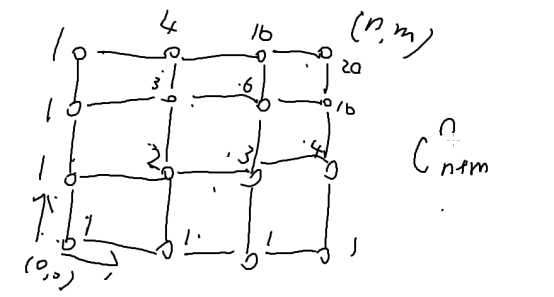
从0走到(n,m)是c(n+m,n)
变式
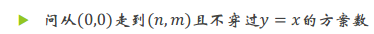
解决的方案是用所有方案减去不合法方案,不合法方案即为穿过了y=x这条线的走法,所以我们找到所有不合法方案穿过这条线的时刻,我们把它第一次不合法的位置的路线沿y=x对称,很容易发现,一定经过(1,0)
下面来点OI系列的

P4369 [Code+#4]组合数问题

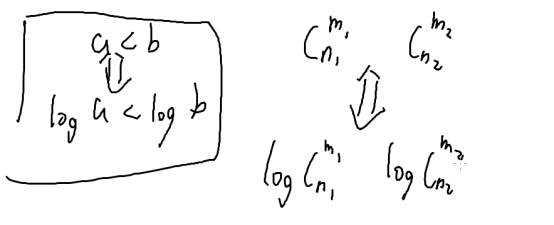
运用对数计算法则,把组合数计算降级为加法运算,在o(1)的情况下比较出来大小

很容易知道最大的组合数一定是杨辉三角最大的一层的最中间的数,而次大的数一定是在最大树的周围四个当中。
Luogu 4370

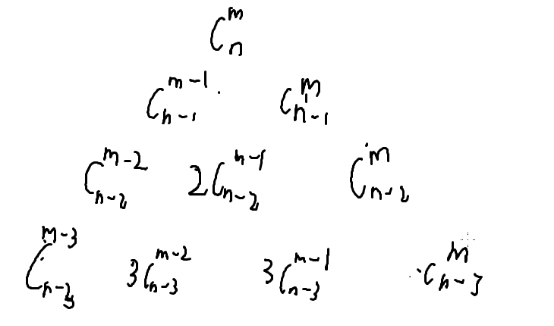
利用杨辉三角进行展开,所以我们可以给出另外一个是式子
把c(n,m)展开k次之后可得到
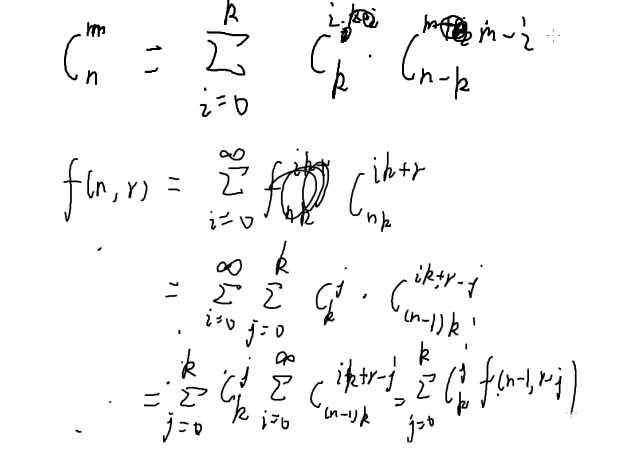
斐波那契数列递归式用矩阵求解


Lucas定理:
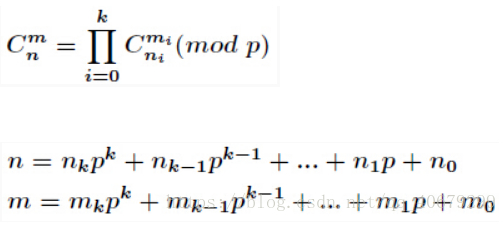
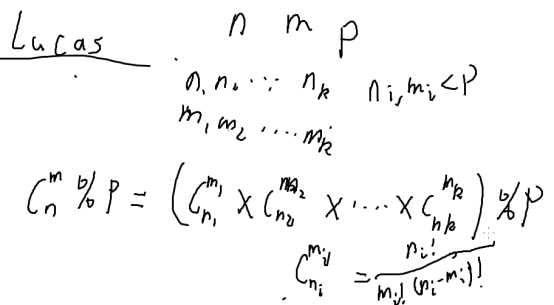
容斥原理:
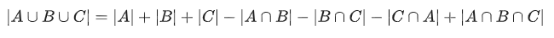
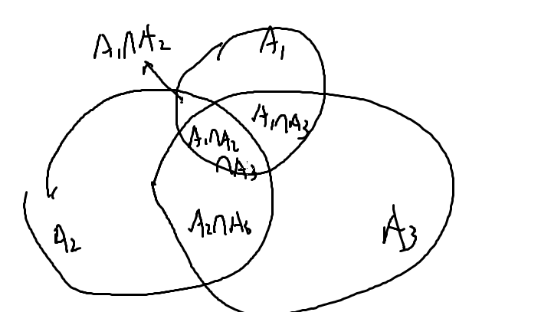
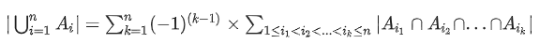
选择k个集合来交
当k是奇数,加上,是偶数的时候,减掉;

维恩图画出来,自然可以求解
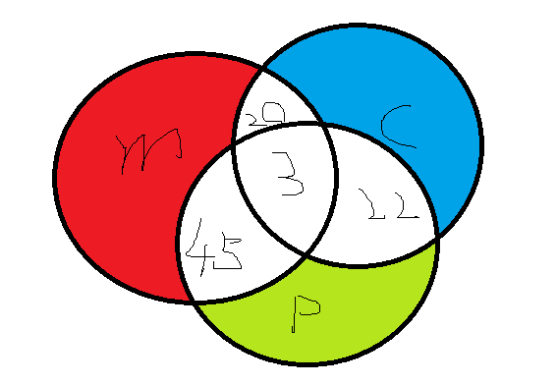
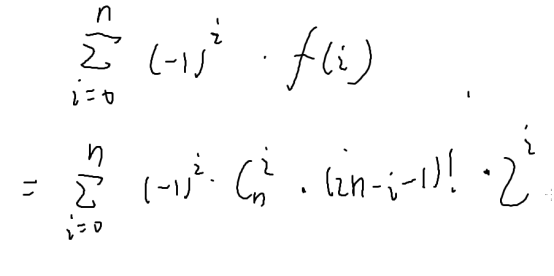
首先我们知道y
最大也就是64,因此我们可以枚举y
很容易知道,y次根号下n就是最大循环到的
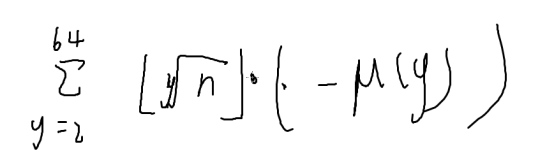
清北学堂Day3的更多相关文章
- 五一培训 清北学堂 DAY3
今天是钟皓曦老师的讲授~ 今天的内容:动态规划 1.动态规划 动态规划很难总结出一套规律 例子:斐波那契数列 0,1,1,2,3,5,8,…… F[0]=0 F[1]=1 F[[n]=f[n-1]+ ...
- 清北学堂2017NOIP冬令营入学测试P4745 B’s problem(b)
清北学堂2017NOIP冬令营入学测试 P4745 B's problem(b) 时间: 1000ms / 空间: 655360KiB / Java类名: Main 背景 冬令营入学测试 描述 题目描 ...
- 清北学堂2017NOIP冬令营入学测试 P4744 A’s problem(a)
清北学堂2017NOIP冬令营入学测试 P4744 A's problem(a) 时间: 1000ms / 空间: 655360KiB / Java类名: Main 背景 冬令营入学测试题,每三天结算 ...
- 济南清北学堂游记 Day 1.
快住手!这根本不是暴力! 刷了一整天的题就是了..上午三道题的画风还算挺正常,估计是第一天,给点水题做做算了.. rqy大佬AK了上午的比赛! 当时我t2暴力写挂,还以为需要用啥奇怪的算法,后来发现, ...
- 清明培训 清北学堂 DAY1
今天是李昊老师的讲授~~ 总结了一下今天的内容: 1.高精度算法 (1) 高精度加法 思路:模拟竖式运算 注意:进位 优化:压位 程序代码: #include<iostream>#in ...
- 7月清北学堂培训 Day 3
今天是丁明朔老师的讲授~ 数据结构 绪论 下面是天天见的: 栈,队列: 堆: 并查集: 树状数组: 线段树: 平衡树: 下面是不常见的: 主席树: 树链剖分: 树套树: 下面是清北学堂课程表里的: S ...
- 清北学堂学习总结day3
小学知识总结 上午篇 •积性函数的卷积公式 (1)(f * g)( n ) = ∑(d|n) f( d ) x g ( n / d ) (2)代码实现 LL f[N], g[N], h[N]; voi ...
- 清北学堂省选刷题冲刺班 Test Day3
目录 2018.3.27 Test T1 T2 T3 考试代码 T2 T3 2018.3.27 Test 时间:8:00~11:30 期望得分:100+60+25=185 实际得分:100+40+25 ...
- 清北学堂2019NOIP提高储备营DAY3
今天是钟神讲课,讲台上照旧摆满了冰红茶 目录时间到: $1. 动态规划 $2. 数位dp $3. 树形dp $4. 区间dp $5. 状压dp $6. 其它dp $1. 动态规划: ·以斐波那契数列为 ...
随机推荐
- QT信号槽connect的第五个参数
用过QT的小伙伴都知道连接信号槽的connect方法,但是这个方法有第五个参数,一般都是用的默认的 connect(th,SIGNAL(started()),tmpmyobject,SLOT(show ...
- 使用 WeihanLi.Npoi 操作 CSV
使用 WeihanLi.Npoi 操作 CSV Intro 最近发现 csv 文件在很多情况下都在使用,而且经过大致了解,csv 格式简单,相比 excel 文件要小很多,读取也很是方便,而且也很通用 ...
- Linux 中NFS服务器的搭建
serve端IP:192.168.2.128 客户端IP:192.168.2.131 server端配置: 1.安装nfs,rpcbind,可以参考Linux 中yum的配置来安装: yum inst ...
- selenium-启动浏览器(二)
selenium下启动浏览器,有两种方法 以 chromedrvier.exe 为例 1. chromedrvier.exe 与 python 启动程序 python.exe 在同一个目录下则可直接使 ...
- SQLServer之修改标量值函数
修改标量值函数注意事项 更改先前通过执行 CREATE FUNCTION 语句创建的现有 Transact-SQL 或 CLR 函数,但不更改权限,也不影响任何相关的函数.存储过程或触发器. 不能用 ...
- 什么是TLB?
TLB:Translation Lookaside Buffer. 根据功能可以译为快表,直译可以翻译为旁路转换缓冲,也可以把它理解成页表缓冲.里面存放的是一些页表文件(虚拟地址到物理地址的转换表). ...
- Bootstrap -- 导航栏样式、分页样式、标签样式、徽章样式
Bootstrap -- 导航栏样式.分页样式.标签样式.徽章样式 1. 使用图标的导航栏 使用导航栏样式: <!DOCTYPE html> <html> <head&g ...
- python之并发编程
一 背景知识 顾名思义,进程即正在执行的一个过程.进程是对正在运行程序的一个抽象. 进程的概念起源于操作系统,是操作系统最核心的概念,也是操作系统提供的最古老也是最重要的抽象概念之一.操作系统的其他所 ...
- Linux内存管理 (11)page引用计数
专题:Linux内存管理专题 关键词:struct page._count._mapcount.PG_locked/PG_referenced/PG_active/PG_dirty等. Linux的内 ...
- Bubble Babble Binary Data Encoding的简介以及bubblepy的安装使用方法
Bubble Babble Binary Data Encoding是由Antti Huima创建的一种编码方法,可以把二进制信息表示为由交替的元音和辅音组成的伪词(pseudo-words),主要用 ...
