[MIT6.006] 3. Insertation Sort, Mege Sort 插入排序，归并排序

关于第2节课《Models of Computation, Document Distance》由于内容过于简单，所以不在这里进行记录，它主要就是讲了Python很多操作是constant time（即无C语言地址指针机制，所以比较费时且耗内存），此外就是谈及了一个文档距离（Document Distance）问题，简单来说就是将文档内所有词形成词袋，用词袋下的特征算余弦距离。需要注意的就是余弦相似度越大，文档就越相似，而余弦距离=1-余弦相似度，因此余弦距离越小，代表文档相似度就越高。

第3节课只讲解了两种排序算法：冒泡排序（课程上用Insertation Sort讲述的思路就是冒泡排序，而实际上Insertation Sort应为插入排序）和归并排序（Merge Sort）。除了这两个还有其他排序方法例如：选择排序，快速排序，插入排序，堆排序，基数排序等等（这些会进行拓展补充或后面的课程会进行讲述）。

对各类排序方法整理如下：

排序算法	时间复杂度
冒泡排序	Ο(n2)
归并排序	Ο(nlog2n)
选择排序	Ο(n2)
插入排序	Ο(n2)
快速排序	极端Ο(n2)，最好Ο(nlog2n)
堆排序	Ο(n)
希尔排序	Ο(ns) (1<s<2)
基数排序	Ο(nlog2(r)m) (r为基数，m为堆数)

注：这里讲解上表中标蓝色和红色的排序算法。红色为课程讲解的算法。

1. 冒泡排序

冒泡排序就是像气泡一样使用pairwise swap成对交换的方式进行排序。下图显示了从左到右冒泡排序的机制：

key不断地移动，然后如果key下的数小于它前面的数，则进行两两交换，并保证换过的数大于左边最近的数，如果不是，那得继续交换，直到key达到最后一个元素，并且是以升序排列的。由于时间复杂度是看最坏情况，那么key的移动得n次，而若第n次对比交换很糟糕（例如1在数列最后面），那么对比得进行n次，最后时间复杂度就为Ο(n²)。

2. 归并排序

如下图，假设要对长度为n的数列A进行排序，归并排序的思想就是Divide&Conquer分开并克服，首先将A着半拆分为左数列L和有数列R，然后分别对L和R进行各自的排序，最后进行L和R的合并操作。

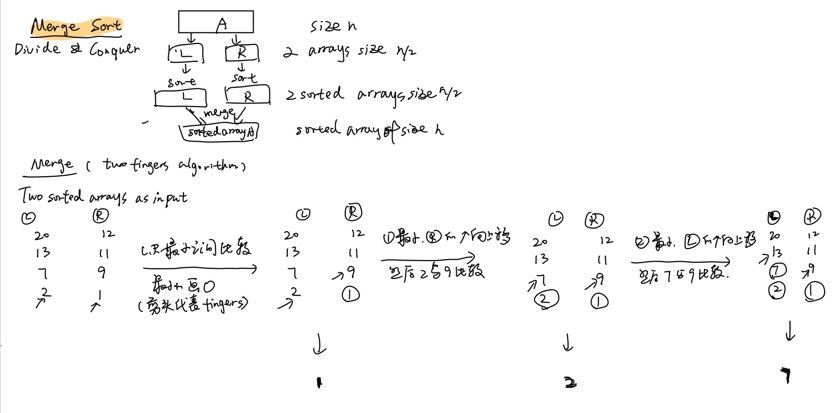
在该课程里，讲师提到了归并排序用的是一种叫Two Fingers双指算法，这里我用上图的列子进行讲述：

1. 如果数列a为[20,13,7,2,12,11,9,1]，将它折半拆为左数列L：[20,13,7,2]，右数列R：[12, 11, 9, 1];
2. 对数列L和R各自进行排序，方法用冒泡排序或其他排序手段都行;
3. 之后用箭头（指代手指）指向数列L和R最小的元素，进行比较，并先输出这个最小的元素，如上图就是min(1,2)=1。
4. 之后在该最小元素下移动箭头至下一个元素，将其与原来另一个数列元素进行比较，如上图就是数列R的箭头移至9, 数列L由于上一步不是最小值，所以箭头不变，则对比箭头所指元素的到min(2, 9)=2，输出结果。重复上述操作箭头到达各自数列末尾。

如下图所示，这里复杂度为Ο(nlog₂n)。这里可以简单的分为两块：（1）二路归并需要进行log₂n次；（2）双指算法对单次二路归并进行n次箭头移动（帮助进行最小值比较操作）。因此就是nlog₂n次。

注：接下来选择排序，插入排序和快速排序的内容整理自《Python程序员面试算法宝典》一书。

3. 选择排序

选择排序的思想很简单：找到一个数列的最小值，然后将它与当前第一个记录交换。时间复杂度为Ο(n²)。

4. 插入排序

插入排序的思想也很简单：初始化一个空数列b，找到数列a中的最小值，然后插入到空数列b中，再不断找最小值，不断插入到数列b末尾即可。时间复杂度为Ο(n²)。

5. 快速排序

关于快排可以看知乎这篇文章的动图：https://zhuanlan.zhihu.com/p/93129029 ， 看完就能理解它的机制，它是一种非常高效的排序算法，主要有三个零件：left左指针，right右指针和base基准数。举个例子如下图所示：

• 首先假设数列a为[6, 3, 7, 4, 1]，则left左指针为数列a最开始的元素6，right右指针为数列b最末端的元素1，base基准数为left左指针6（注意这个base基准数从头到尾都不改动的）。

1. 先从right指向的数与base对比：

• 如果right<base，则将right值替换left值，然后left向右移一位，同时right值替换为空值，且right指针位置不变，然后让left此时指的数与base对比。
• 如果right>base，则将right值替换right值（即保持不变），然后right向左移一位，同时left值替换为空值，且left指针位置不变，然后让right此时指的数与base对比。

1. 重复上述操作，直到左右指针重叠，此时就直接将base值放入重叠位置即可。

总结上面的就是：先右开始对比，之后'小于则替换left并移left，然后新left对比base'或’大于则替换right并移right，然后新right对比base‘, left和right重合后用base替换。它的时间复杂度取决于base值真实在排序后的位置，如果base刚好为排序中间的位置，时间复杂度为Ο(nlog₂n)，如果base为数列最大值或最小值，则为Ο(n²)。