树堆（Treap）学习笔记 2020.8.12

如果一棵二叉排序树的节点插入的顺序是随机的，那么这样建立的二叉排序树在大多数情况下是平衡的，可以证明，其高度期望值为 \(O( \log_2 n )\)。即使存在一些极端情况，但是这种情况发生的概率很小。而且这样建立的二叉排序树的操作很方便，不必像伸展树那样通过伸展操作来保持数的平衡，也不必像 AVL 树、红黑树等结构那样，为了达到平衡而进行各种复杂的旋转操作。变成复杂度低了，正确率就很高，这对有限的竞赛时间和紧张的竞赛考场是很重要的。

Treap 就是一种满足堆的性质的二叉排序树。在保持二叉排序树基本性质不变的同时，为每一个节点设置一个随机的权值，权值满足堆的性质，其结构和效果相当于按随机顺序插入节点而建立的二叉排序树。它的实现简单，支持伸展树的大部分操作，而且效率高于伸展树。

“Treap”一词是由“Tree”和“Heap”而来。Treap本身是一棵二叉排序树，它的左子树和右子树也分别是一棵Treap。

和一般的二叉排序树不同的是，Treap记录了一个额外的数据域 —— 优先级。Treap在以关键字构成二叉排序树的同时，优先级还满足堆的性质（这篇随笔假设采用小根堆）。但是，Treap和堆有一点不同：堆必须是完全二叉树，而Treap并不一定要求是。

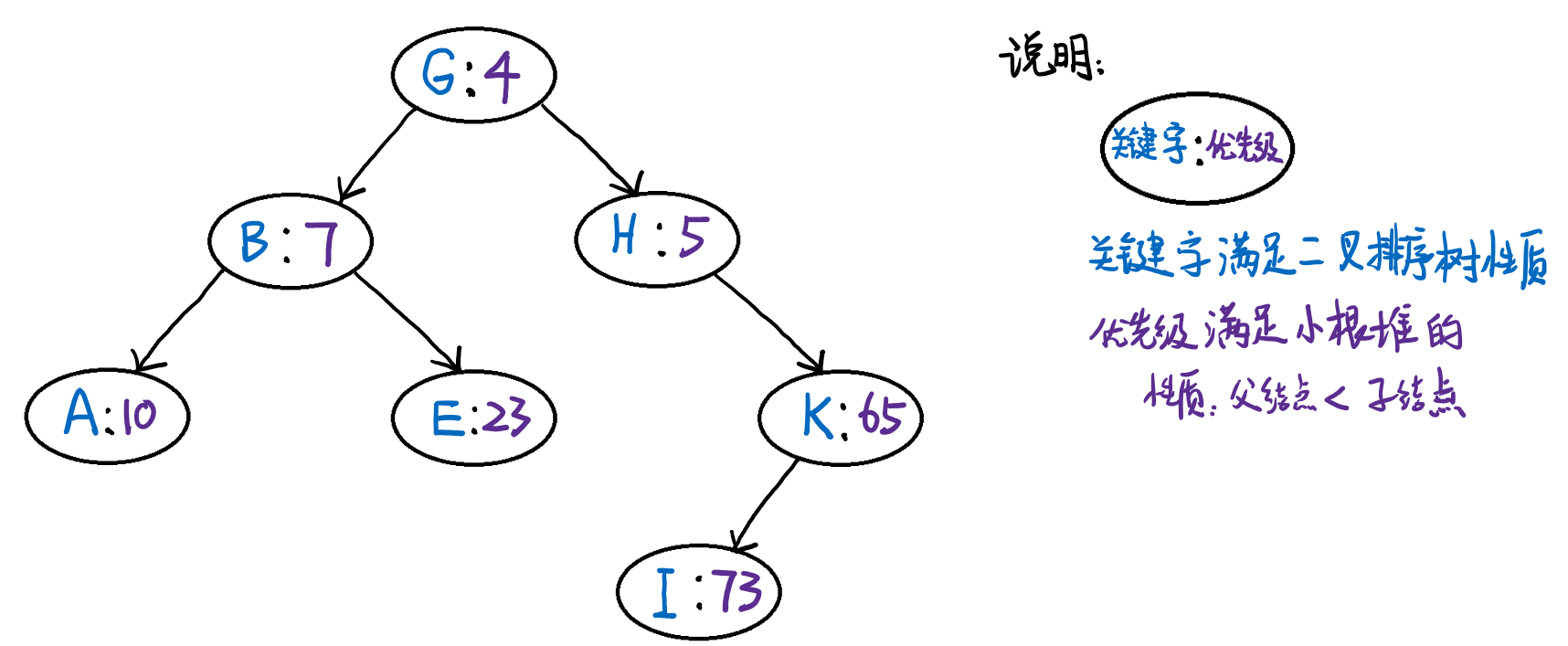
如图所示就是一个 Treap 结构，其按关键字中序遍历的结果是：ABEGHIK，而且优先级满足小根堆。

1. Treap的基本操作

让 Treap 同时满足两个性质的具体做法是：首先让它满足二叉排序树的性质，再通过旋转操作（左旋或右旋），在不破坏二叉排序树性质的同时满足堆的性质。Treap 旋转操作主要通过操作某个父节点和它的一个子节点，让子节点上去，父节点下来。

下图是 Treap 的左旋和右旋操作的示意图：

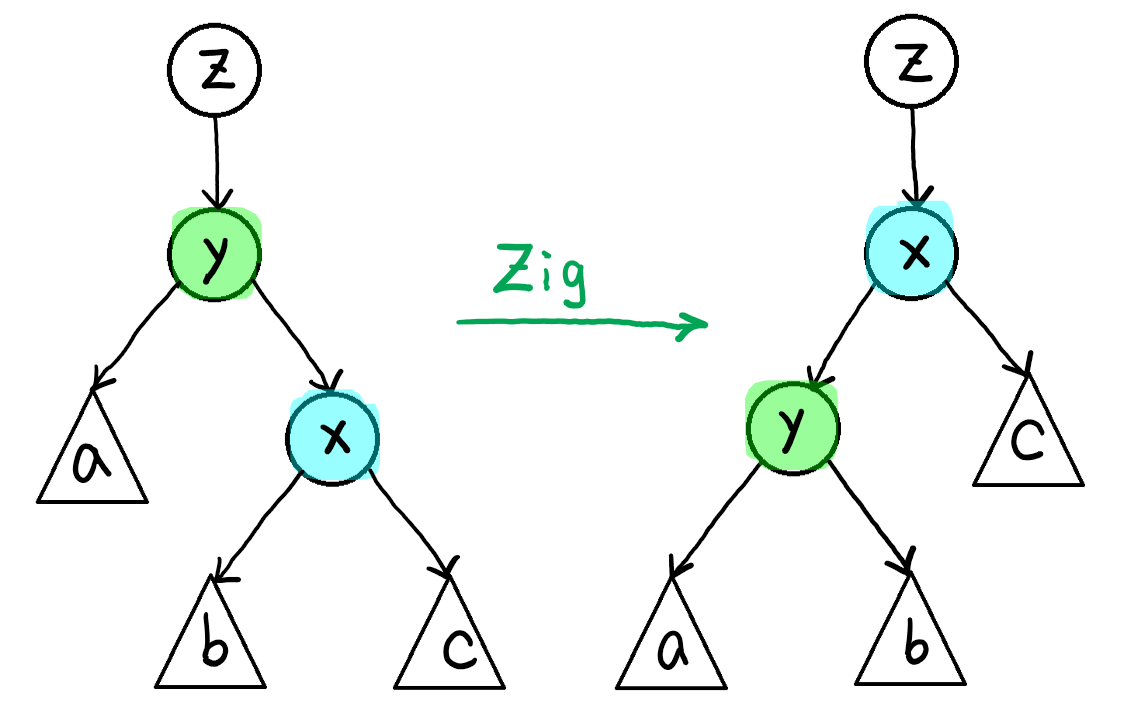
Treap的左旋操作

Treap的右旋操作

（一个疑惑：为什么Splay的左旋叫Zag，右旋叫Zig；而Treap的左旋叫Zig，右旋叫Zag？）

在 Zig 和 Zag 操作中，可以看到 \(a,b,c,x,y\) 之间的大小关系没有发生改变。

由于是二叉搜索树，满足根节点的关键字 \(\gt\) 左子树；\(\lt\) 右子树，所以

对于上图中的左旋（Zig）操作，翻转前

\[A \lt y \lt B \lt x \lt C
\]

（其中 \(A,B,C\) 分别表示以 \(a,b,c\) 为根节点的子树中的所有元素）

翻转后仍然满足这个性质。

对于上图中国的右旋（Zag）操作，翻转前

\[A \lt x \lt B \lt y \lt C
\]

翻转后仍然满足这个性质。

通过左旋和右旋两种旋转操作，一个节点可以在Treap中自由地上下移动，而且节点的上下移动很容易和堆节点的上调和下调对应起来。下面介绍Treap的一些基本操作。

1. 查找、求最大值、求最小值

这三个操作和二叉排序树的做法一样，但是由于Treap的随机化结构，可以证明在Treap中查找、求最大值、求最小值的时间复杂度都是 \(O(h)\) 的，其中，\(h\) 表示树的高度。

2. 插入

先给节点随机分配一个优先级，然后和二叉排序树的节点插入一样，把要插入的节点插入到一个叶子上，然后维护堆的性质，即如果当前节点的优先级比根小就旋转（如果当前节点是根的左二子就右旋，如果当前节点是根的右儿子就左旋）。

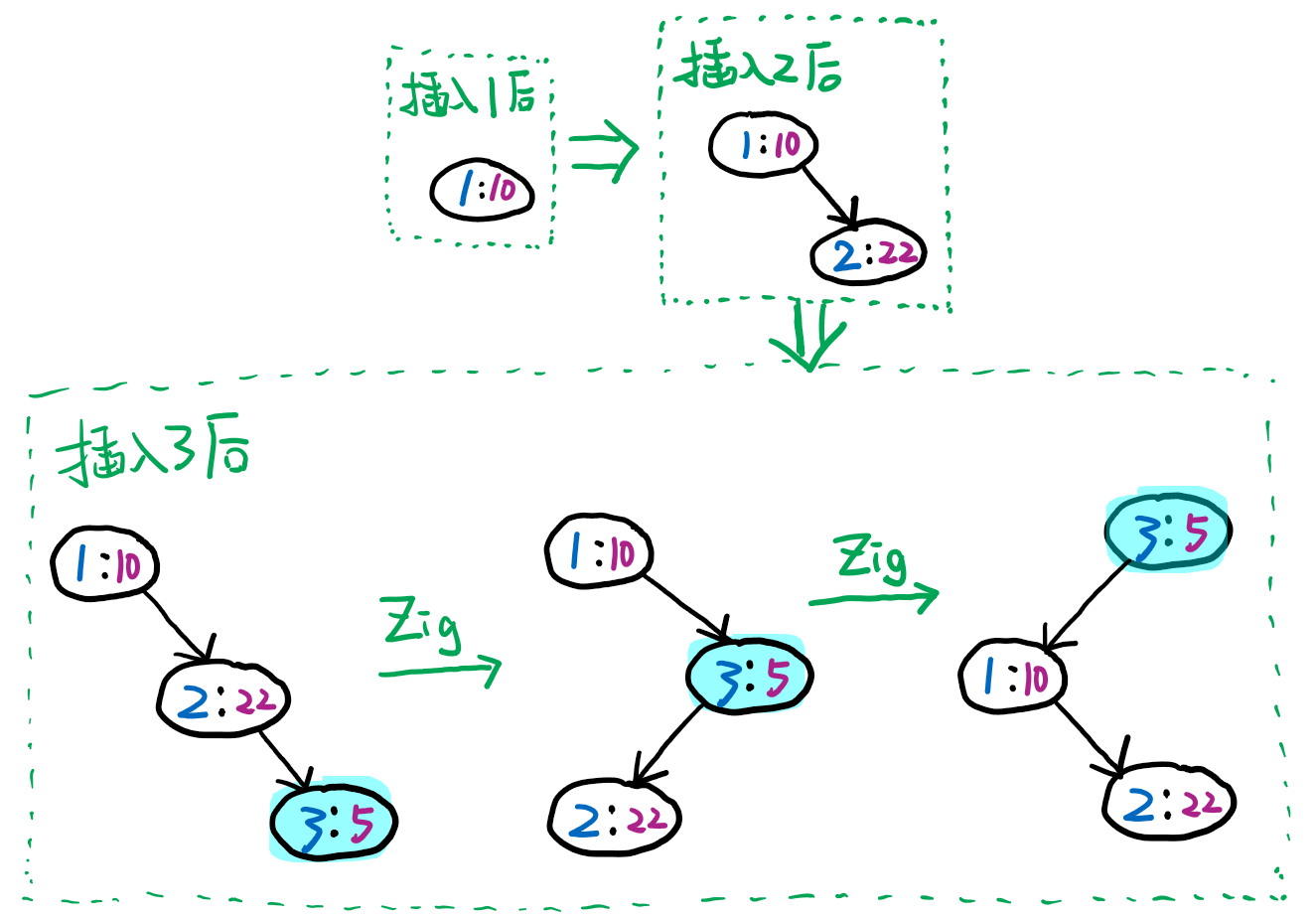
假设要插入的数依次为 \(1,2,3,4,5,6\)，通过随机函数得到的优先级分别为 \(10,22,5,80,37,45\)，则依次插入节点的过程如下：

插入 \(1\) 和 \(2\) 时都没有影响堆的性质，所以不需要进行旋转维护。

\((3:5)\) 插入后，由于 \(5\) 比 \(22\)、\(10\) 都小，所以要进行两次旋转操作，把 \((3:5)\) 调整到最上面，保证了优先级符合堆性质。

插入 \(4\) 不需要进行旋转。

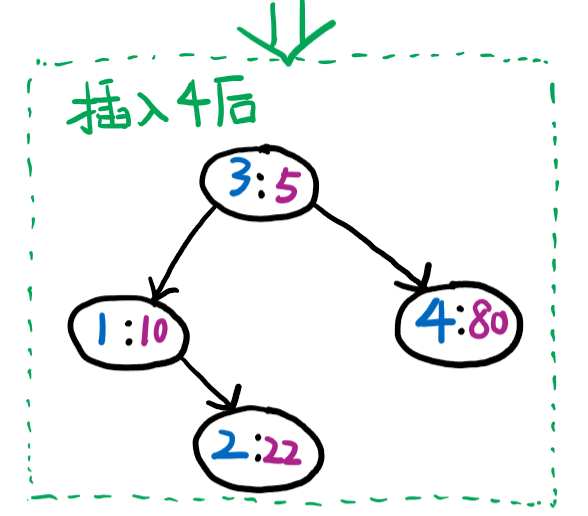
插入 \(5\) 之后要进行一次左旋。

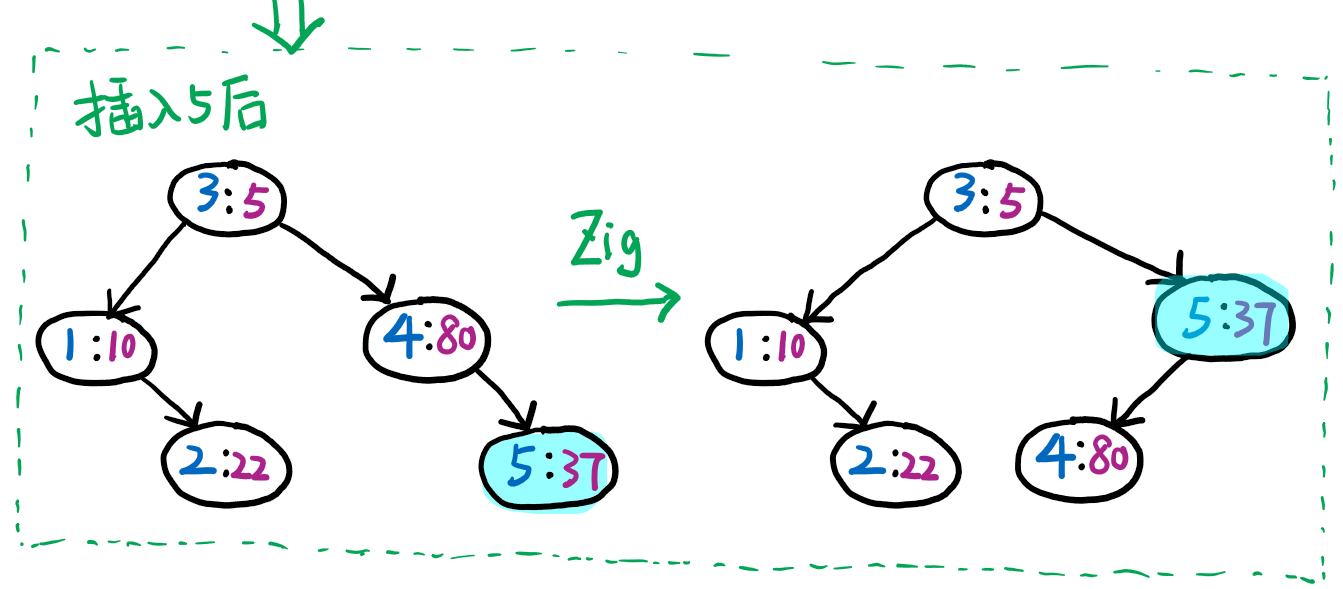
插入 \(6\) 之后不需要进行旋转。

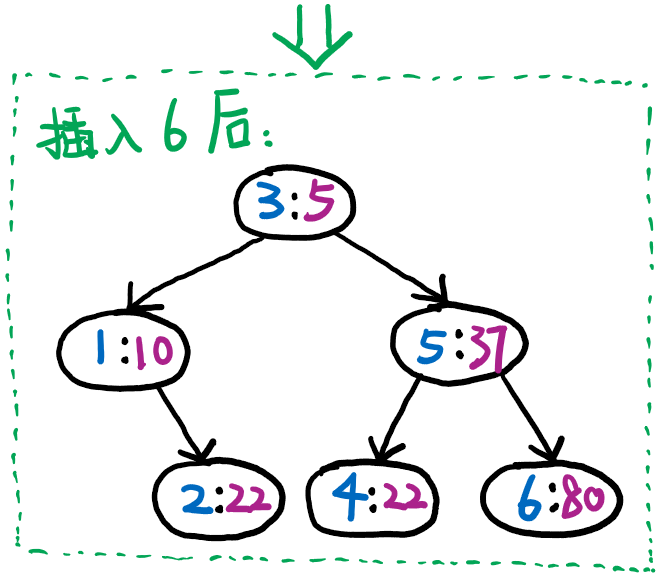
然后就完成了整棵树的插入。

通过观察，不难发现，如果把每个元素按照优先级大小的顺序（在上例中，即按照 \(3,1,2,5,4,6\) 的顺序）一次插入二叉排序树，形成的树和以上插入调整后的结果完全一致。这就是 Treap 的作用，使得数据插入实现了无关于数据本身的随机性，其效果与把数据打乱后插入完全相同，这使得它几乎能应用于所有需要使用平衡树的地方。

如果把插入的过程写成递归形式，只要在递归调用完成后判断是否满足堆的性质，如果不满足就继续旋转，实现起来也非常容易。由于旋转操作的时间复杂度是 \(O(1)\)，最多只要进行 \(h\) 次旋转（\(h\) 是树的高度），所以总的时间复杂度为 \(O(h)\)。

3. 删除

有了旋转操作之后，Treap的删除比二叉排序树还要简单。因为Treap满足堆性质，所以我们只需要把要删除的节点旋转成叶节点，然后直接删除就可以了。具体的做法就是每次找到优先级小的孩子，向与其相反方向旋转，直到那个节点被旋转成了叶节点，然后直接删除即可。

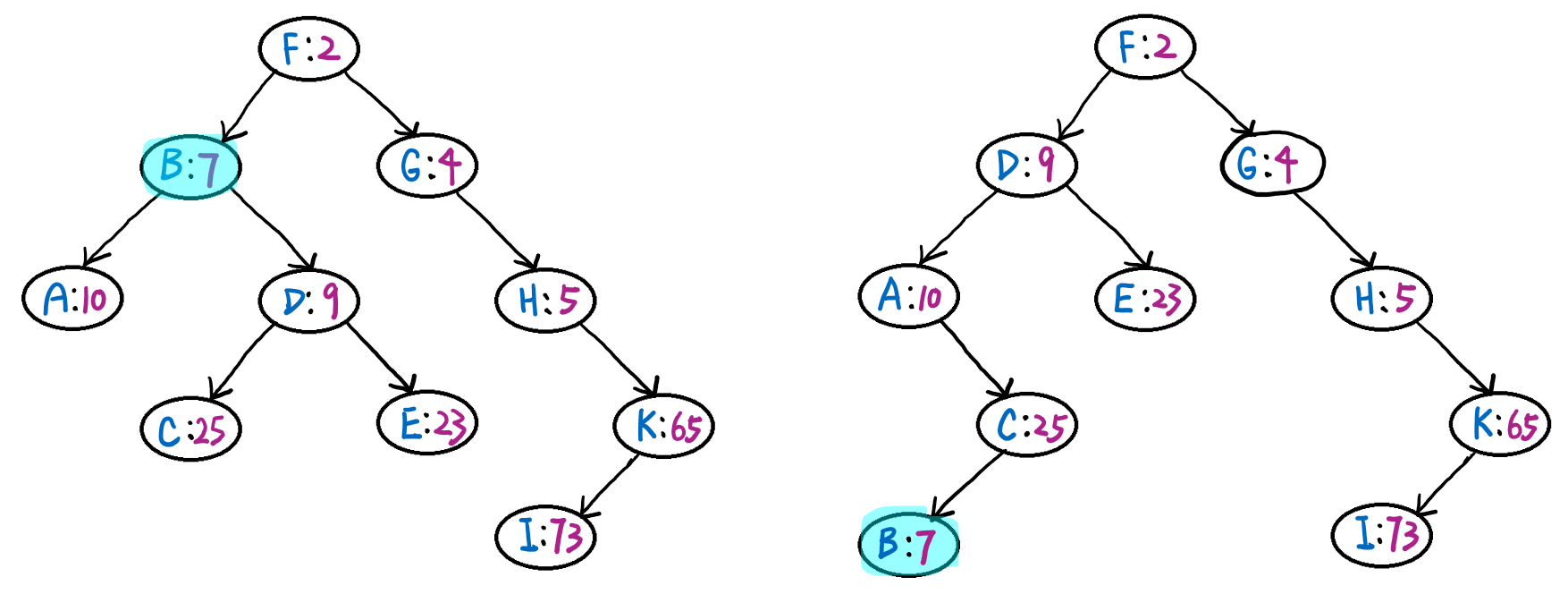
例如，要删除下图（左图）中的节点 \((B:7)\)，旋转的结果如下图（右图）所示，再删除节点 \((B:7)\)。删除最多进行 \(h\) 次旋转，所以删除的时间复杂度是 \(O(h)\)。

4. 分离

要把一个Treap按大小分成两个Treap，只需要在分开的位置强行增加一个虚拟节点（设好优先级），然后依据优先级旋转至根节点再将其删除掉，左右两棵子树就是两个Treap了。根据二叉排序树的性质，这时左子树的所有节点都小于右子树的节点。分离的时间复杂度相当于一次插入操作的时间复杂度，也是 \(O(h)\)。

5. 合并

合并是指把两棵平衡树合并成一棵平衡树，其中第一棵树的所有节点都必须小于或等于第二棵树中的所有节点，这也是上面的分离操作的结果所满足的条件。Treap合并操作的过程和分离过程相反，只要曾姐一个虚拟的根，把两棵树分别作为左右子树，然后再把根删除就可以了。合并的时间复杂度和删除一样，也是 \(O(h)\)。

Treap的算法实现

首先定义一些需要的数据，即声明好结构体的功能：

int val[maxn],          // 关键字
    priority[maxn],     // 优先级
    lson[maxn],         // 左二子编号
    rson[maxn],         // 右儿子编号
    p[maxn],            // 父节点编号
    sz;                 // 元素个数
struct Treap {
    int rt;     // 根节点编号
    void zig(int x);    // 左旋
    void zag(int x);    // 右旋
    void func_rotate(int x); // 旋转（左旋+右旋）
    void add(int v);    // 插入一个值v
    int func_find(int v);   // 查找值为v的元素
    void del(int v);    // 删除一个值为v的元素
    int getMin();   // 获得最小值
    int getMax();   // 获得最大值
    int getPre(int v);  // 获得前趋（值<=v的最大元素）
    int getSuc(int v);  // 获得后继（值>=v的最小元素）
} tree;

然后定义左旋和右旋的功能：

// 左旋
void Treap::zig(int x) {
    int y = p[x], z = p[y];
    assert(y && rson[y] == x);
    if (rt == y) rt = x;    // 更新rt
    int b = lson[x];
    rson[y] = b;
    p[b] = y;
    lson[x] = y;
    p[y] = x;
    p[x] = z;
    if (z) {
        if (lson[z] == y) lson[z] = x;
        else rson[z] = x;
    }
}

// 右旋
void Treap::zag(int x) {
    int y = p[x], z = p[y];
    assert(y && lson[y] == x);
    if (rt == y) rt = x;    // 更新rt
    int b = rson[x];
    lson[y] = b;
    p[b] = y;
    rson[x] = y;
    p[y] = x;
    p[x] = z;
    if (z) {
        if (lson[z] == y) lson[z] = x;
        else rson[z] = x;
    }
}

左旋与右旋的实现需要注意以下几个问题：

1. 针对子节点 \(x\) 或者父节点 \(y\) 都可以（我的实现中都是针对子节点 \(x\) 的）；
2. 旋转的前提是： \(x\) 必须得有父节点，也就是说不能把根节点通过旋转向上调；
3. 要注意有些子树可能是不存在的，不存在的节点定义成 \(0\) 即可；
4. 如果节点有父节点，子节点指向新的父节点后，原先的父节点的子节点信息也得改变，父子关系的调整是双向的 —— 我不是你的儿子了，那么同时你也不是我的父亲了。

由于左旋和右旋的目的都是为了将子节点 \(x\) 向上调整一层，所以我们可以封装好一个 func_rotate 函数用于统一左旋和右旋操作：

// 旋转（左旋+右旋）
void Treap::func_rotate(int x) {
    assert(p[x]);
    if (x == rson[p[x]]) zig(x);
    else zag(x);
}

插入：

// 插入一个值v
void Treap::add(int v) {
    val[++sz] = v;
    priority[sz] = rand();
    if (!rt) rt = sz;
    else {
        int x = rt;
        while (true) {
            if (val[x] >= v) {
                if (lson[x]) x = lson[x];
                else {
                    lson[x] = sz;
                    p[sz] = x;
                    break;
                }
            }
            else {
                if (rson[x]) x = rson[x];
                else {
                    rson[x] = sz;
                    p[sz] = x;
                    break;
                }
            }
        }
        x = sz;
        while (p[x] && priority[x] < priority[p[x]]) func_rotate(x);
    }
}

查询：

// 查找值为v的元素
int Treap::func_find(int v) {
    if (!rt) return 0;
    int x = rt;
    while (true) {
        if (val[x] == v) return x;
        else if (val[x] > v) {
            if (lson[x]) x = lson[x];
            else return 0;
        }
        else {  // val[x] < v
            if (rson[x]) x = rson[x];
            else return 0;
        }
    }
}

删除：

// 删除一个值为v的元素
void Treap::del(int v) {
    int x = func_find(v);
    if (!x) return;
    while (lson[x] || rson[x]) {
        if (!rson[x]) func_rotate(lson[x]);
        else if (!lson[x]) func_rotate(rson[x]);
        else if (priority[lson[x]] < priority[rson[x]]) func_rotate(lson[x]);
        else func_rotate(rson[x]);
    }
    // 循环退出时x变成了叶子节点，删除它
    if (x == rt) {  // 叶子节点==根节点 --> 就1个节点
        rt = 0;
        return;
    }
    int y = p[x];
    if (y) {
        if (lson[y] == x) lson[y] = 0;
        else rson[y] = 0;
    }
    p[x] = 0;   // 这句不写也没关系
}

求最小值：

// 获得最小值
int Treap::getMin() {
    int x = rt;
    while (lson[x]) x = lson[x];
    return x;
}

求最大值：

// 获得最大值
int Treap::getMax() {
    int x = rt;
    while (rson[x]) x = rson[x];
    return x;
}

求前趋：

// 获得前趋（值<=v的最大元素）
int Treap::getPre(int v) {
    if (!rt) return 0;
    int ans = 0, x = rt;
    while (x) {
        if (val[x] <= v) {
            if (ans == 0 || val[ans] < val[x]) ans = x;
            x = rson[x];
        }
        else x = lson[x];
    }
    return ans;
}

求后继：

// 获得后继（值>=v的最小元素）
int Treap::getSuc(int v) {
    if (!rt) return 0;
    int ans = 0, x = rt;
    while (x) {
        if (val[x] >= v) {
            if (ans == 0 || val[ans] > val[x]) ans = x;
            x = lson[x];
        }
        else x = rson[x];
    }
    return ans;
}

完整的代码如下（对应《怪物仓库管理员（二）》）：

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1000010;
int val[maxn],          // 关键字
    priority[maxn],     // 优先级
    lson[maxn],         // 左二子编号
    rson[maxn],         // 右儿子编号
    p[maxn],            // 父节点编号
    sz;                 // 元素个数
struct Treap {
    int rt;     // 根节点编号
    void zig(int x);    // 左旋
    void zag(int x);    // 右旋
    void func_rotate(int x); // 旋转（左旋+右旋）
    void add(int v);    // 插入一个值v
    int func_find(int v);   // 查找值为v的元素
    void del(int v);    // 删除一个值为v的元素
    int getMin();   // 获得最小值
    int getMax();   // 获得最大值
    int getPre(int v);  // 获得前趋（值<=v的最大元素）
    int getSuc(int v);  // 获得后继（值>=v的最小元素）
} tree;

// 左旋
void Treap::zig(int x) {
    int y = p[x], z = p[y];
    assert(y && rson[y] == x);
    if (rt == y) rt = x;    // 更新rt
    int b = lson[x];
    rson[y] = b;
    p[b] = y;
    lson[x] = y;
    p[y] = x;
    p[x] = z;
    if (z) {
        if (lson[z] == y) lson[z] = x;
        else rson[z] = x;
    }
}

// 右旋
void Treap::zag(int x) {
    int y = p[x], z = p[y];
    assert(y && lson[y] == x);
    if (rt == y) rt = x;    // 更新rt
    int b = rson[x];
    lson[y] = b;
    p[b] = y;
    rson[x] = y;
    p[y] = x;
    p[x] = z;
    if (z) {
        if (lson[z] == y) lson[z] = x;
        else rson[z] = x;
    }
}

// 旋转（左旋+右旋）
void Treap::func_rotate(int x) {
    assert(p[x]);
    if (x == rson[p[x]]) zig(x);
    else zag(x);
}

// 插入一个值v
void Treap::add(int v) {
    val[++sz] = v;
    priority[sz] = rand();
    if (!rt) rt = sz;
    else {
        int x = rt;
        while (true) {
            if (val[x] >= v) {
                if (lson[x]) x = lson[x];
                else {
                    lson[x] = sz;
                    p[sz] = x;
                    break;
                }
            }
            else {
                if (rson[x]) x = rson[x];
                else {
                    rson[x] = sz;
                    p[sz] = x;
                    break;
                }
            }
        }
        x = sz;
        while (p[x] && priority[x] < priority[p[x]]) func_rotate(x);
    }
}

// 查找值为v的元素
int Treap::func_find(int v) {
    if (!rt) return 0;
    int x = rt;
    while (true) {
        if (val[x] == v) return x;
        else if (val[x] > v) {
            if (lson[x]) x = lson[x];
            else return 0;
        }
        else {  // val[x] < v
            if (rson[x]) x = rson[x];
            else return 0;
        }
    }
}

// 删除一个值为v的元素
void Treap::del(int v) {
    int x = func_find(v);
    if (!x) return;
    while (lson[x] || rson[x]) {
        if (!rson[x]) func_rotate(lson[x]);
        else if (!lson[x]) func_rotate(rson[x]);
        else if (priority[lson[x]] < priority[rson[x]]) func_rotate(lson[x]);
        else func_rotate(rson[x]);
    }
    // 循环退出时x变成了叶子节点，删除它
    if (x == rt) {  // 叶子节点==根节点 --> 就1个节点
        rt = 0;
        return;
    }
    int y = p[x];
    if (y) {
        if (lson[y] == x) lson[y] = 0;
        else rson[y] = 0;
    }
    p[x] = 0;   // 这句不写也没关系
}

// 获得最小值
int Treap::getMin() {
    int x = rt;
    while (lson[x]) x = lson[x];
    return x;
}

// 获得最大值
int Treap::getMax() {
    int x = rt;
    while (rson[x]) x = rson[x];
    return x;
}

// 获得前趋（值<=v的最大元素）
int Treap::getPre(int v) {
    if (!rt) return 0;
    int ans = 0, x = rt;
    while (x) {
        if (val[x] <= v) {
            if (ans == 0 || val[ans] < val[x]) ans = x;
            x = rson[x];
        }
        else x = lson[x];
    }
    return ans;
}

// 获得后继（值>=v的最小元素）
int Treap::getSuc(int v) {
    if (!rt) return 0;
    int ans = 0, x = rt;
    while (x) {
        if (val[x] >= v) {
            if (ans == 0 || val[ans] > val[x]) ans = x;
            x = lson[x];
        }
        else x = rson[x];
    }
    return ans;
}

int n, op, x;

int main() {
    scanf("%d", &n);
    while (n --) {
        scanf("%d", &op);
        if (op != 3 && op != 4) scanf("%d", &x);
        if (op == 1) tree.add(x);
        else if (op == 2) tree.del(x);
        else if (op == 3) printf("%d\n", val[tree.getMin()]);
        else if (op == 4) printf("%d\n", val[tree.getMax()]);
        else if (op == 5) printf("%d\n", val[tree.getPre(x)]);
        else printf("%d\n", val[tree.getSuc(x)]);
    }
    return 0;
}